What Is 3/10 Of 150
saludintensiva
Sep 16, 2025 · 5 min read
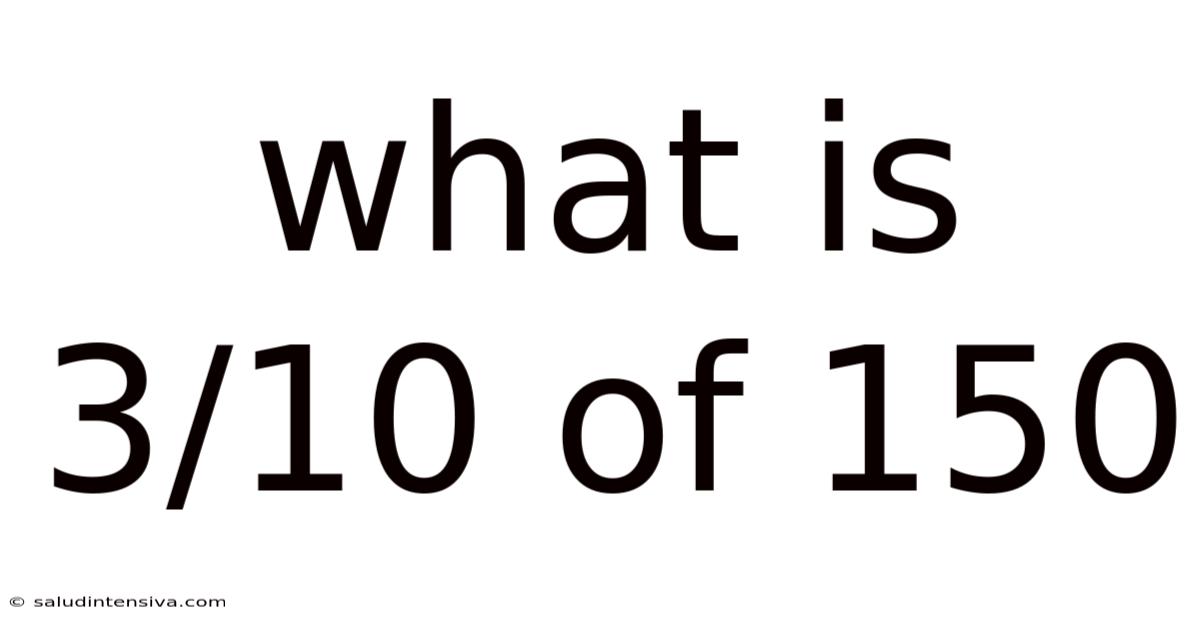
Table of Contents
What is 3/10 of 150? A Deep Dive into Fractions and Percentages
Finding 3/10 of 150 might seem like a simple arithmetic problem, but it opens the door to understanding fundamental concepts in mathematics, particularly fractions, decimals, and percentages. This seemingly straightforward calculation underpins many real-world applications, from calculating discounts to understanding financial proportions. This article will not only answer the question directly but also explore the underlying principles, offering a comprehensive guide for learners of all levels.
Understanding Fractions: The Building Blocks
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. In our problem, 3/10 means we have 3 parts out of a total of 10 equal parts.
Method 1: Direct Calculation
The most straightforward method to find 3/10 of 150 is to perform the calculation directly:
- Multiply the numerator by the whole number: 3 x 150 = 450
- Divide the result by the denominator: 450 / 10 = 45
Therefore, 3/10 of 150 is 45.
Method 2: Converting the Fraction to a Decimal
Another approach involves converting the fraction 3/10 into its decimal equivalent. This method is particularly helpful when working with calculators or when dealing with more complex fractions.
- Convert the fraction to a decimal: 3/10 = 0.3
- Multiply the decimal by the whole number: 0.3 x 150 = 45
Again, we arrive at the answer: 45.
Method 3: Finding 1/10 and then Multiplying
This method breaks down the problem into smaller, more manageable steps. It's a great approach for visualizing the process and improving understanding.
- Find 1/10 of 150: 150 / 10 = 15
- Multiply the result by the numerator: 15 x 3 = 45
This reinforces that 3/10 is simply three times the value of 1/10. The answer, once again, is 45.
Connecting Fractions, Decimals, and Percentages
This problem also allows us to explore the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
- Fraction: 3/10
- Decimal: 0.3 (obtained by dividing the numerator by the denominator)
- Percentage: 30% (obtained by multiplying the decimal by 100)
Understanding this interconnectivity is crucial for solving various mathematical problems and interpreting data in real-world contexts. For instance, a 30% discount on a $150 item would also result in a $45 reduction.
Real-World Applications: Beyond the Classroom
The ability to calculate fractions of a whole number has widespread applications in numerous fields:
- Finance: Calculating interest, discounts, taxes, and profit margins all involve working with fractions and percentages.
- Retail: Determining discounts, calculating sales tax, and understanding profit margins are essential for retailers.
- Construction: Measuring materials, calculating proportions of ingredients in concrete mixes, and understanding building plans require fractional calculations.
- Cooking: Adjusting recipes, scaling ingredients up or down, and understanding ratios rely heavily on fractions.
- Science: Many scientific calculations, particularly in chemistry and physics, involve working with fractions and proportions.
Expanding the Understanding: Working with More Complex Fractions
While this article focuses on a relatively simple fraction, the principles discussed can be applied to more complex scenarios. Let's consider finding 7/15 of 225:
- Multiply the numerator by the whole number: 7 x 225 = 1575
- Divide the result by the denominator: 1575 / 15 = 105
Therefore, 7/15 of 225 is 105.
This example demonstrates the scalability of the methods discussed earlier. Regardless of the complexity of the fraction, the fundamental approach remains consistent: multiply the numerator by the whole number and then divide the result by the denominator.
Frequently Asked Questions (FAQ)
Q: What if the denominator doesn't divide evenly into the whole number?
A: If the denominator doesn't divide evenly, you'll get a decimal or a fraction as a result. For example, 2/3 of 150 is (2 x 150) / 3 = 100. This is perfectly acceptable and often represents a more realistic scenario in real-world problems.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators can significantly simplify the process, particularly for more complex fractions or large numbers.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. For example, 3/10 = 0.3 x 100 = 30%.
Q: What are some common mistakes to avoid?
A: A common mistake is reversing the numerator and the denominator. Always ensure you're multiplying by the correct number. Another mistake is forgetting the order of operations (multiplication before division).
Conclusion: Mastering Fractions - A Foundation for Success
Finding 3/10 of 150, while seemingly a simple problem, provides a valuable opportunity to reinforce fundamental mathematical concepts. Understanding fractions, decimals, and percentages is crucial for success in various academic and professional fields. By mastering these principles, individuals equip themselves with essential tools for tackling a wide range of real-world challenges. The methods discussed in this article—direct calculation, decimal conversion, and finding a unit fraction—offer flexible approaches to solving such problems, promoting a deeper understanding of the underlying mathematical principles. Remember that practice is key to solidifying these concepts and building confidence in tackling more complex calculations. So, grab your pen and paper, or fire up your calculator, and continue exploring the fascinating world of fractions!
Latest Posts
Latest Posts
-
Surface Area Prisms And Pyramids
Sep 16, 2025
-
6 8 As A Percentage
Sep 16, 2025
-
Gcf Of 28 And 16
Sep 16, 2025
-
90 Days From May 15
Sep 16, 2025
-
Subtract Whole Numbers With Fractions
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/10 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.