What Is 3 2 Squared
saludintensiva
Sep 11, 2025 · 5 min read
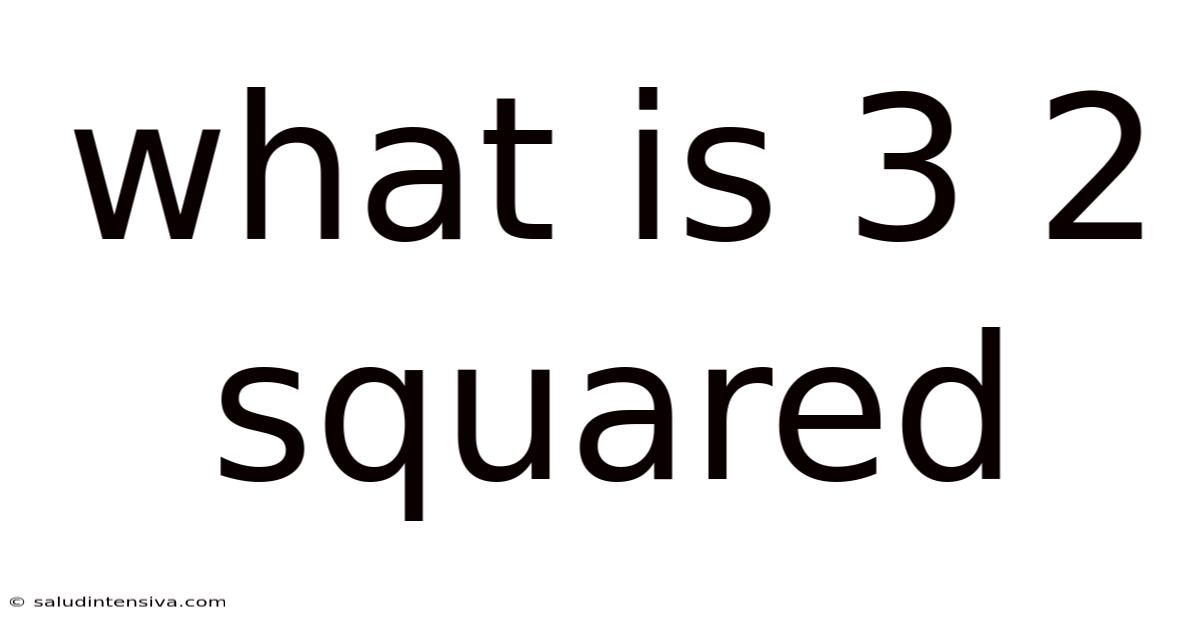
Table of Contents
Decoding "3 2 Squared": Understanding Exponents and Order of Operations
The phrase "3 2 squared" might seem straightforward at first glance, but it subtly highlights the crucial importance of understanding mathematical notation and the order of operations. This article will delve into the meaning of "3 2 squared," explaining not only the calculation itself but also the underlying principles of exponents and the widely used PEMDAS/BODMAS acronym. We will explore common misunderstandings and provide a clear, step-by-step approach to solving similar problems. By the end, you'll have a solid grasp of this concept and be able to tackle more complex mathematical expressions with confidence.
Understanding Exponents
Before we tackle "3 2 squared," let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's written as a small superscript number to the right of the base. For example:
- 2² (2 squared) means 2 x 2 = 4
- 3³ (3 cubed) means 3 x 3 x 3 = 27
- 5⁴ (5 to the power of 4) means 5 x 5 x 5 x 5 = 625
The base number is the number being multiplied, and the exponent tells us how many times to perform the multiplication.
Interpreting "3 2 Squared"
The phrase "3 2 squared" is ambiguous without proper mathematical notation. It could be interpreted in two ways:
- (3 x 2)²: This interpretation suggests we first multiply 3 and 2, and then square the result.
- 3 x 2²: This interpretation implies we square 2 first and then multiply the result by 3.
The ambiguity highlights the necessity of using clear and unambiguous mathematical notation. To avoid confusion, we should always use parentheses to indicate the order of operations.
The Order of Operations: PEMDAS/BODMAS
To correctly solve mathematical expressions, we need to follow the order of operations. This is often remembered using the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order:
- Parentheses/Brackets: Perform any calculations inside parentheses or brackets first.
- Exponents/Orders: Evaluate any exponents or powers.
- Multiplication and Division: Perform multiplication and division from left to right.
- Addition and Subtraction: Perform addition and subtraction from left to right.
Solving "(3 x 2)²"
Following PEMDAS/BODMAS, let's solve the first interpretation, "(3 x 2)²":
- Parentheses: First, we perform the calculation inside the parentheses: 3 x 2 = 6
- Exponents: Next, we square the result: 6² = 6 x 6 = 36
Therefore, (3 x 2)² = 36
Solving "3 x 2²"
Now, let's solve the second interpretation, "3 x 2²":
- Exponents: First, we evaluate the exponent: 2² = 2 x 2 = 4
- Multiplication: Next, we perform the multiplication: 3 x 4 = 12
Therefore, 3 x 2² = 12
The Crucial Difference: Why Notation Matters
The difference between 36 and 12 clearly demonstrates the importance of precise mathematical notation. Without parentheses to clarify the order of operations, the expression "3 2 squared" is inherently ambiguous. This emphasizes the need for careful writing and interpretation of mathematical expressions to avoid errors and ensure accurate results.
Expanding the Concept: More Complex Examples
Let's explore more complex examples to solidify our understanding of exponents and order of operations:
Example 1: (5 + 2)² - 4 x 3
- Parentheses: (5 + 2) = 7
- Exponents: 7² = 49
- Multiplication: 4 x 3 = 12
- Subtraction: 49 - 12 = 37
Therefore, (5 + 2)² - 4 x 3 = 37
Example 2: 4³ + (6 - 2)² x 5
- Parentheses: (6 - 2) = 4
- Exponents: 4³ = 64 and 4² = 16
- Multiplication: 16 x 5 = 80
- Addition: 64 + 80 = 144
Therefore, 4³ + (6 - 2)² x 5 = 144
These examples highlight the sequential application of PEMDAS/BODMAS. Always remember to tackle parentheses/brackets first, followed by exponents, then multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Common Mistakes and How to Avoid Them
A frequent mistake is neglecting the order of operations, leading to incorrect results. For instance, incorrectly calculating "3 x 2²" as (3 x 2)² = 36 is a common error. Remember, exponents take precedence over multiplication.
Another common mistake is misinterpreting notation. Always use parentheses to clarify the intended order of operations, especially when dealing with more complex expressions. This prevents ambiguity and ensures accurate calculations.
Frequently Asked Questions (FAQ)
Q: What is the difference between squaring and cubing a number?
A: Squaring a number means raising it to the power of 2 (multiplying it by itself once), while cubing a number means raising it to the power of 3 (multiplying it by itself twice).
Q: Can negative numbers be squared or cubed?
A: Yes, negative numbers can be raised to any power. Remember that when squaring a negative number, the result is always positive (because a negative multiplied by a negative is positive). Cubing a negative number results in a negative number.
Q: How can I improve my understanding of exponents and order of operations?
A: Practice is key! Work through numerous examples, starting with simpler problems and gradually increasing the complexity. Use online resources, textbooks, and practice worksheets to reinforce your understanding. Pay close attention to notation and the correct application of PEMDAS/BODMAS.
Conclusion
Understanding "3 2 squared" requires a clear grasp of exponents and the order of operations. The ambiguity of the phrase highlights the importance of using precise mathematical notation to avoid confusion. By consistently applying PEMDAS/BODMAS and using parentheses to clarify the order of operations, you can accurately solve such expressions and tackle more complex mathematical problems with confidence. Remember to practice regularly to solidify your understanding and avoid common pitfalls. Mastering these fundamental concepts is crucial for success in mathematics and related fields. With consistent effort and practice, you will develop a strong foundation in these essential mathematical skills.
Latest Posts
Latest Posts
-
8 000 Meters To Feet
Sep 12, 2025
-
22 9 As A Mixed Number
Sep 12, 2025
-
1 88 Meters To Feet
Sep 12, 2025
-
4 10 In A Decimal
Sep 12, 2025
-
Convert 1 5 To A Fraction
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 2 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.