What Is 3/4 Of 8
saludintensiva
Sep 19, 2025 · 5 min read
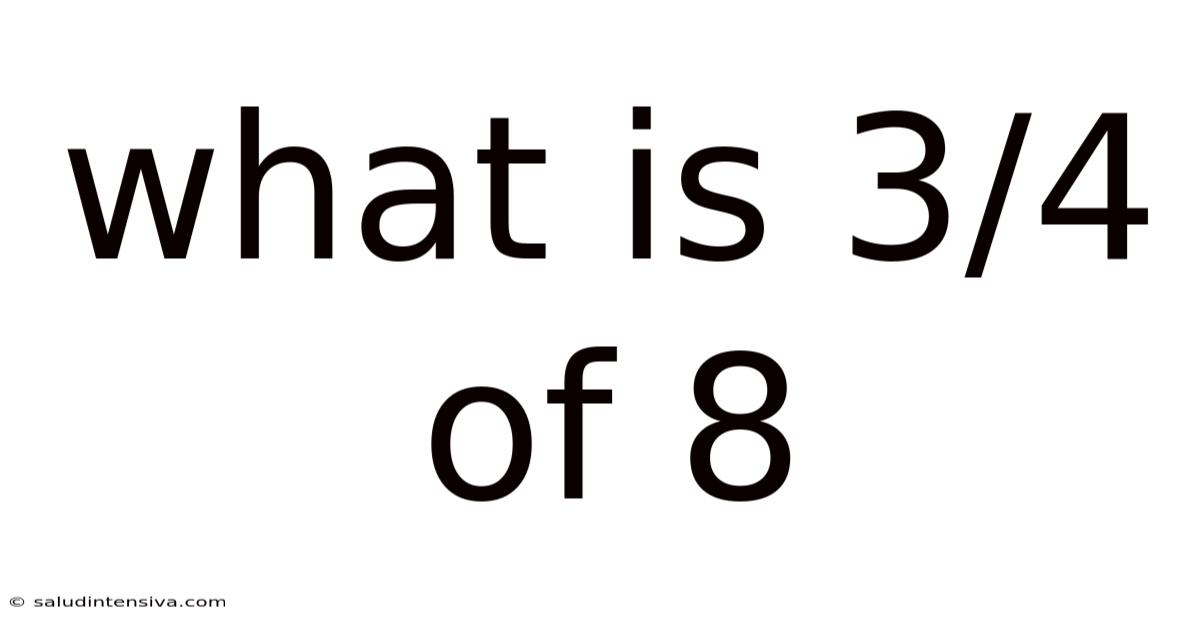
Table of Contents
What is 3/4 of 8? Unpacking Fractions and Multiplication
Finding 3/4 of 8 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to solve this seemingly basic equation unlocks a deeper understanding of fractions, multiplication, and their practical applications in various fields. This article will not only show you how to calculate 3/4 of 8 but also delve into the underlying mathematical principles, explore different solution methods, and discuss real-world examples where this type of calculation is crucial.
Understanding Fractions: A Quick Refresher
Before we dive into calculating 3/4 of 8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
Fractions can be:
- Proper fractions: Where the numerator is smaller than the denominator (e.g., 1/2, 3/4).
- Improper fractions: Where the numerator is equal to or larger than the denominator (e.g., 5/4, 8/3).
- Mixed numbers: A combination of a whole number and a proper fraction (e.g., 1 1/2, 2 3/4).
Method 1: Converting the Fraction to a Decimal
One straightforward way to calculate 3/4 of 8 is by first converting the fraction 3/4 into its decimal equivalent. To do this, we simply divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Now, we multiply this decimal by 8:
0.75 x 8 = 6
Therefore, 3/4 of 8 is 6.
Method 2: Using Multiplication Directly
Alternatively, we can solve this problem directly using multiplication with fractions. Remember that "of" in mathematics often signifies multiplication. So, "3/4 of 8" can be written as:
(3/4) x 8
To multiply a fraction by a whole number, we can treat the whole number as a fraction with a denominator of 1:
(3/4) x (8/1)
Now, we multiply the numerators together and the denominators together:
(3 x 8) / (4 x 1) = 24/4
Finally, we simplify the resulting fraction by dividing the numerator by the denominator:
24 ÷ 4 = 6
Again, we arrive at the answer: 3/4 of 8 is 6.
Method 3: Visual Representation
Visualizing the problem can be incredibly helpful, especially for those who are new to fractions. Imagine a pizza cut into 4 equal slices. Each slice represents 1/4 of the whole pizza. If we have 3 slices, we have 3/4 of the pizza.
Now, let's say we have 8 pizzas, each cut into 4 slices. To find 3/4 of 8 pizzas, we would take 3 slices from each of the 8 pizzas. This would give us a total of 3 x 8 = 24 slices. Since each pizza has 4 slices, we can divide the total number of slices by 4 to find the number of whole pizzas:
24 slices ÷ 4 slices/pizza = 6 pizzas
Thus, 3/4 of 8 pizzas is 6 pizzas.
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of 3/4 of 8 has far-reaching applications in everyday life and various professions. Here are a few examples:
- Cooking and Baking: Recipes often require fractional amounts of ingredients. If a recipe calls for 3/4 of a cup of sugar and you want to double the recipe (making it for 8 people instead of 4), you need to calculate 3/4 of 8 cups.
- Construction and Engineering: Calculating the required amount of materials for a project often involves fractions. For example, if a construction project needs 8 tons of concrete and only 3/4 of the total amount is needed for the foundation, the calculation is needed.
- Finance and Budgeting: Many financial calculations involve percentages, which are simply fractions expressed as parts of 100. Understanding fractions is essential for budgeting, calculating discounts, or understanding interest rates.
- Data Analysis and Statistics: Fractions and proportions are fundamental to data analysis and statistical calculations. Interpreting data often involves calculating percentages and proportions.
Extending the Concept: Working with Other Fractions
Understanding how to find 3/4 of 8 allows us to extend this knowledge to calculate other fractional parts of numbers. The same methods—converting to decimals, direct multiplication, or visual representation—can be applied. For example:
- Finding 2/5 of 15: (2/5) x 15 = (2 x 15) / 5 = 30/5 = 6
- Finding 5/6 of 18: (5/6) x 18 = (5 x 18) / 6 = 90/6 = 15
- Finding 7/8 of 24: (7/8) x 24 = (7 x 24) / 8 = 168/8 = 21
The key is to understand the underlying principle of multiplying the numerator by the whole number and then dividing the result by the denominator.
Frequently Asked Questions (FAQs)
Q1: What if the fraction and the whole number don't simplify easily?
A1: Even if the fraction and whole number don't simplify neatly, the methods described above still work. You may end up with a fraction as your answer, or you might need to use a calculator to perform the division.
Q2: Can I use a calculator to solve this problem?
A2: Absolutely! Calculators are helpful tools for performing these calculations, especially with more complex fractions or larger numbers.
Q3: Why is understanding fractions important?
A3: Fractions are the building blocks of many mathematical concepts, including decimals, percentages, ratios, and proportions. A strong understanding of fractions is crucial for success in mathematics and its applications in various fields.
Conclusion: Mastering Fractions – One Step at a Time
Calculating 3/4 of 8 might seem trivial at first glance. However, by exploring this simple problem, we’ve delved into the fundamental principles of fractions, multiplication, and their widespread applications. Understanding different methods for solving fractional problems, coupled with visual representations, builds a solid foundation for tackling more complex mathematical challenges. The ability to confidently work with fractions is a crucial skill for academic success and navigating the numerical aspects of everyday life. Remember to practice regularly, and soon you’ll find working with fractions as easy as pie!
Latest Posts
Latest Posts
-
Calculating The Mean In R
Sep 20, 2025
-
2x 2 5x 2 Factor
Sep 20, 2025
-
What Is A 77 Grade
Sep 20, 2025
-
144 Cm To Feet Inches
Sep 20, 2025
-
Convert 50 Ft To Meters
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.