What Is 3/5 Of 5
saludintensiva
Sep 22, 2025 · 5 min read
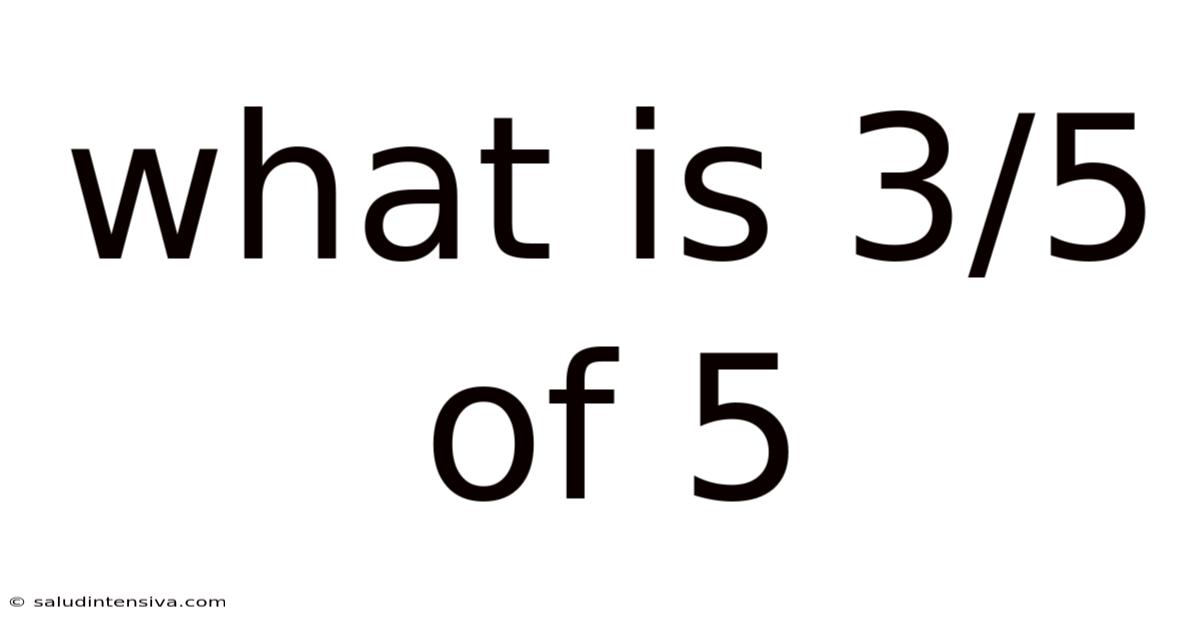
Table of Contents
What is 3/5 of 5? Unpacking Fractions and Multiplication
Finding 3/5 of 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly straightforward equation reveals a deeper understanding of fractions, multiplication, and their practical applications in various fields. This article will not only solve the problem but delve into the underlying mathematical principles, explore different approaches to solving similar problems, and even touch upon real-world applications. We'll also address common misconceptions and frequently asked questions to ensure a comprehensive understanding.
Understanding Fractions: The Building Blocks
Before we tackle the problem of finding 3/5 of 5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/5, 3 is the numerator and 5 is the denominator. This means we're dealing with 3 parts out of a total of 5 equal parts.
Solving 3/5 of 5: A Step-by-Step Approach
The phrase "of" in mathematics usually signifies multiplication. Therefore, finding 3/5 of 5 is equivalent to calculating (3/5) * 5. There are several ways to approach this calculation:
Method 1: Direct Multiplication
The most straightforward method is to multiply the fraction by the whole number directly:
(3/5) * 5 = (3 * 5) / 5 = 15 / 5 = 3
Here, we multiply the numerator (3) by the whole number (5), keeping the denominator the same. Then, we simplify the resulting fraction by dividing the numerator by the denominator. The answer is 3.
Method 2: Simplifying Before Multiplication
We can simplify the calculation by canceling out common factors before multiplication. Notice that the denominator (5) and the whole number (5) share a common factor of 5. We can cancel these out:
(3/5) * 5 = 3 * (5/5) = 3 * 1 = 3
This method simplifies the calculation, making it easier to solve, especially with larger numbers.
Method 3: Visual Representation
For a more intuitive understanding, we can visualize the problem. Imagine a whole divided into 5 equal parts. Finding 3/5 of 5 means taking 3 out of these 5 parts. Since each part represents 1 (5 parts make up the whole 5), taking 3 parts gives us a total of 3.
Extending the Concept: Working with Different Fractions and Numbers
The methods described above can be applied to finding a fraction of any number. Let's consider a few examples:
-
Finding 2/3 of 9: (2/3) * 9 = (2 * 9) / 3 = 18 / 3 = 6. Alternatively, we can simplify: (2/3) * 9 = 2 * (9/3) = 2 * 3 = 6.
-
Finding 1/4 of 12: (1/4) * 12 = (1 * 12) / 4 = 12 / 4 = 3. Or, simplified: (1/4) * 12 = 1 * (12/4) = 1 * 3 = 3.
-
Finding 5/8 of 24: (5/8) * 24 = (5 * 24) / 8 = 120 / 8 = 15. Simplified: (5/8) * 24 = 5 * (24/8) = 5 * 3 = 15.
These examples demonstrate the versatility of these methods in solving various fraction multiplication problems.
Real-World Applications: Fractions in Everyday Life
Understanding fractions and how to calculate them is crucial in various aspects of daily life:
-
Cooking and Baking: Recipes often use fractions to specify ingredient amounts (e.g., 1/2 cup of flour, 2/3 cup of sugar).
-
Shopping and Budgeting: Calculating discounts, sales tax, or splitting bills often involves working with fractions and percentages (which are essentially fractions expressed as hundredths).
-
Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fractions and decimals.
-
Data Analysis and Statistics: Fractions and percentages are fundamental tools for interpreting data and presenting statistical information.
Common Misconceptions and How to Avoid Them
Several common misconceptions can lead to errors when working with fractions:
-
Incorrect Order of Operations: Remember that multiplication of fractions and whole numbers follows the standard order of operations. Don't add or subtract before multiplying.
-
Confusing Numerator and Denominator: Always pay close attention to which number is the numerator and which is the denominator. Inverting them will lead to an incorrect answer.
-
Forgetting to Simplify: Always simplify the resulting fraction to its lowest terms for the most accurate and concise answer.
Frequently Asked Questions (FAQs)
-
Q: Can I use decimals instead of fractions? A: Yes, you can convert the fraction 3/5 to its decimal equivalent (0.6) and then multiply by 5: 0.6 * 5 = 3. Both methods yield the same result.
-
Q: What if the whole number isn't divisible by the denominator? A: You'll still use the same multiplication method. You might end up with an improper fraction (where the numerator is larger than the denominator), which you can then convert to a mixed number (a whole number and a proper fraction). For example, finding 2/3 of 7 would be (2/3) * 7 = 14/3 = 4 2/3.
-
Q: How can I improve my understanding of fractions? A: Practice is key! Work through various examples, use visual aids like diagrams or fraction bars, and try solving problems with different types of fractions and whole numbers.
Conclusion: Mastering Fractions for a Deeper Mathematical Understanding
Finding 3/5 of 5, seemingly a simple problem, serves as a gateway to understanding the broader world of fractions and their applications. By mastering the techniques and concepts discussed here, you'll not only solve similar problems with ease but also develop a more robust mathematical foundation. Remember to practice regularly, understand the underlying principles, and don't be afraid to use different approaches to solidify your understanding. With consistent effort, you can confidently tackle more complex fraction problems and appreciate their vital role in various fields. The journey to mastering fractions is not merely about getting the right answer; it’s about developing a deeper appreciation for the elegance and power of mathematics in our daily lives.
Latest Posts
Latest Posts
-
Graph Cube Root Of X
Sep 22, 2025
-
What Is 6 3 4
Sep 22, 2025
-
Gcf Of 28 And 56
Sep 22, 2025
-
1 Yd To Sq Ft
Sep 22, 2025
-
Number Generator 1 To 30
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/5 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.