What Is 3 Times 1/2
saludintensiva
Sep 17, 2025 · 5 min read
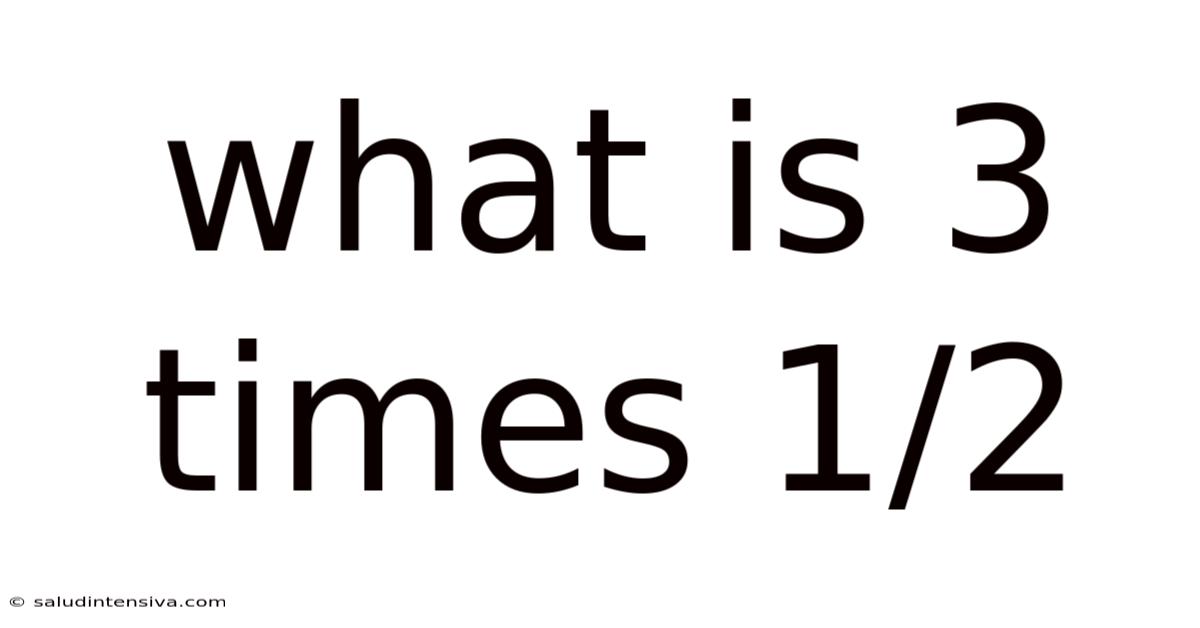
Table of Contents
What is 3 Times 1/2? Unpacking Multiplication with Fractions
This article explores the seemingly simple question, "What is 3 times 1/2?", delving far beyond the immediate answer to provide a comprehensive understanding of fractional multiplication. We'll cover the basic calculation, explore different methods for solving it, examine the underlying mathematical concepts, and even touch upon real-world applications. This guide is designed for learners of all levels, from those just grasping the basics of fractions to those looking to solidify their understanding of fundamental arithmetic.
Understanding the Basics: Fractions and Multiplication
Before we tackle the specific problem, let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. It's composed of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
Multiplication, in its simplest form, is repeated addition. When we say "3 times 1/2," we're essentially asking, "What is the result of adding 1/2 to itself three times?"
Method 1: Repeated Addition
The most intuitive method to solve 3 times 1/2 is through repeated addition:
1/2 + 1/2 + 1/2 = 3/2
Since the denominators are the same, we simply add the numerators. The result, 3/2, is an improper fraction – the numerator is larger than the denominator.
Method 2: Multiplying a Whole Number by a Fraction
Another approach involves directly multiplying the whole number (3) by the numerator of the fraction (1), while keeping the denominator the same:
3 x (1/2) = (3 x 1) / 2 = 3/2
This method is a shortcut, streamlining the process of repeated addition. It demonstrates the fundamental principle of multiplying a whole number by a fraction: multiply the whole number by the numerator and retain the original denominator.
Method 3: Visual Representation
Visual aids can significantly enhance understanding, especially when dealing with fractions. Imagine a pizza cut into two equal slices. "1/2" represents one of these slices. "3 times 1/2" means having three of these slices. Together, these three halves make up 1 ½ pizzas. This visual representation directly corresponds to the numerical answer, 3/2.
Converting Improper Fractions to Mixed Numbers
The answer 3/2 is an improper fraction. It's often more convenient to express it as a mixed number, which combines a whole number and a proper fraction. To convert 3/2 to a mixed number, we perform the division:
3 ÷ 2 = 1 with a remainder of 1
This means 3/2 equals 1 and 1/2. Therefore, 3 times 1/2 is equal to 1 ½.
The Commutative Property and its Application
The commutative property of multiplication states that the order of the factors does not affect the product. In other words, a x b = b x a. This applies to fractions as well. Therefore, 3 x (1/2) is the same as (1/2) x 3. This can be useful when working with more complex fractional multiplications.
Extending the Concept: Multiplying Fractions by Fractions
The principles discussed above can be extended to multiplying fractions by other fractions. To multiply two fractions, simply multiply the numerators together and the denominators together. For example:
(1/2) x (1/3) = (1 x 1) / (2 x 3) = 1/6
This seemingly simple operation underlies many complex mathematical concepts and applications.
Real-World Applications: Where Fractions Matter
Fractions are not just abstract mathematical concepts; they are integral to numerous real-world situations:
-
Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Understanding fractional multiplication is crucial for scaling recipes up or down.
-
Measurement: Many measurements involve fractions (e.g., 2 1/2 inches, 3/4 of a kilometer). Accurate calculations necessitate proficiency in fractional arithmetic.
-
Finance: Interest rates, discounts, and stock prices are often expressed as fractions or percentages (which are essentially fractions with a denominator of 100).
-
Construction and Engineering: Precise measurements and calculations are vital in these fields, requiring a strong understanding of fractions and their manipulation.
Beyond the Basics: Further Exploration
This foundational understanding of multiplying whole numbers by fractions opens doors to more advanced concepts:
-
Decimal Equivalents: Fractions can be converted to decimals (e.g., 3/2 = 1.5). Working with decimals can sometimes simplify calculations.
-
Percentage Calculations: Percentages are closely related to fractions. Understanding the relationship between fractions and percentages is essential for various applications.
-
Algebraic Manipulation: Fractions are fundamental to algebraic equations and manipulations. A solid grasp of fractional arithmetic is crucial for success in algebra.
Frequently Asked Questions (FAQs)
Q: Can I multiply fractions without using repeated addition?
A: Yes, the most efficient method is to multiply the whole number by the numerator and keep the denominator the same (as shown in Method 2).
Q: What if the fraction is a mixed number?
A: First, convert the mixed number to an improper fraction. Then, apply the multiplication method described above. For example, to calculate 3 times 1 1/2, first convert 1 1/2 to 3/2, and then multiply 3 by 3/2, which equals 9/2 or 4 1/2.
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to mathematics and have wide-ranging applications in various aspects of life, from everyday tasks to complex scientific calculations. Mastering fractions builds a strong foundation for more advanced mathematical concepts.
Q: Are there any online resources or tools that can help me practice?
A: Many websites and educational apps offer interactive exercises and tutorials on fractions and multiplication.
Conclusion: Mastering the Fundamentals
The question "What is 3 times 1/2?" seemingly presents a simple arithmetic problem. However, exploring its solution reveals a wealth of fundamental mathematical concepts related to fractions and multiplication. Understanding these concepts isn't just about getting the right answer; it's about building a strong mathematical foundation that will serve you well in various aspects of life. By mastering the principles outlined in this article, you'll not only confidently answer questions about fractional multiplication but also develop a deeper appreciation for the beauty and practicality of mathematics. Remember, consistent practice and a willingness to explore different approaches are key to mastering any mathematical concept. So, keep practicing and expanding your knowledge!
Latest Posts
Latest Posts
-
Gcf For 40 And 60
Sep 17, 2025
-
What Is 35c In F
Sep 17, 2025
-
What Time Is 15 13
Sep 17, 2025
-
Gcf Of 20 And 36
Sep 17, 2025
-
Lcm For 4 And 12
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Times 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.