What Is 3 Times 1/5
saludintensiva
Sep 15, 2025 · 6 min read
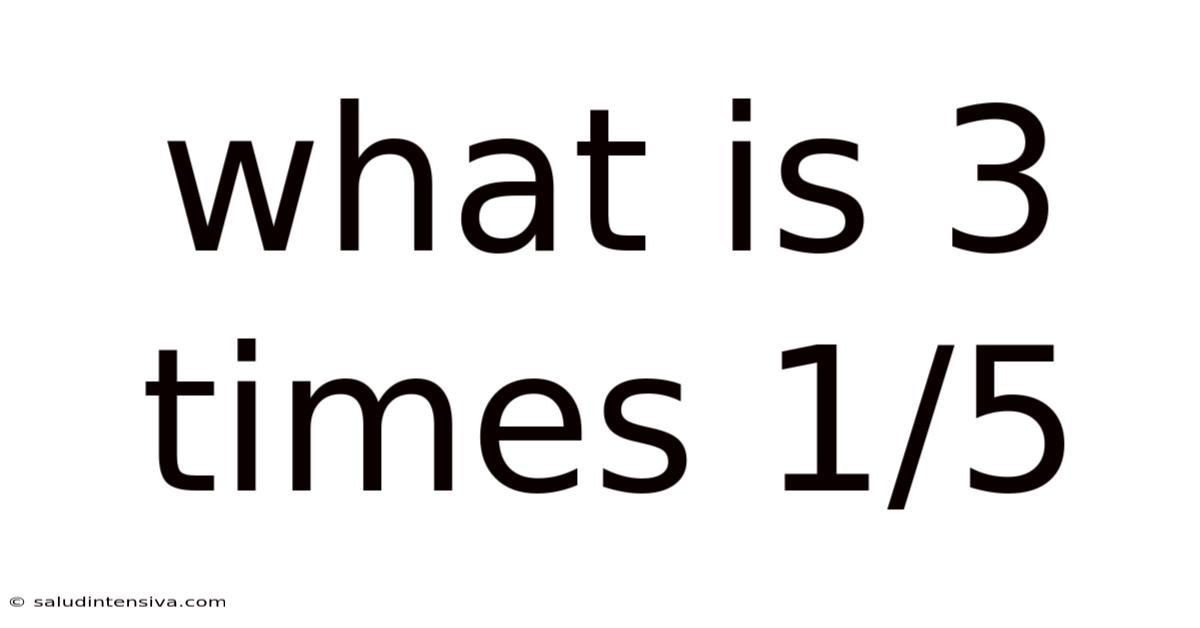
Table of Contents
What is 3 Times 1/5? Understanding Fractions and Multiplication
This article explores the seemingly simple question, "What is 3 times 1/5?", but expands it to delve into the fundamental concepts of fraction multiplication, offering a comprehensive understanding suitable for learners of all levels. We’ll break down the process step-by-step, explore the underlying mathematical principles, and even address some common misconceptions. By the end, you'll not only know the answer but also possess a solid grasp of how to tackle similar problems involving fractions and whole numbers.
Understanding Fractions: A Quick Refresher
Before diving into the multiplication, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering.
For example, in the fraction 1/5, the denominator (5) tells us the whole is divided into five equal parts. The numerator (1) indicates we're looking at just one of those parts. Visually, imagine a pie cut into five slices; 1/5 represents a single slice.
Multiplying Fractions and Whole Numbers: The Process
Now, let's tackle the core question: What is 3 times 1/5? This is essentially asking us to add 1/5 to itself three times: 1/5 + 1/5 + 1/5. However, there's a more efficient method for multiplying fractions and whole numbers.
The process is straightforward:
-
Represent the whole number as a fraction: Any whole number can be expressed as a fraction with a denominator of 1. In this case, 3 can be written as 3/1.
-
Multiply the numerators: Multiply the top numbers (numerators) of both fractions together. In our example, this is 3 * 1 = 3.
-
Multiply the denominators: Multiply the bottom numbers (denominators) of both fractions together. In our example, this is 1 * 5 = 5.
-
Simplify the resulting fraction (if possible): The result of multiplying 3/1 and 1/5 is 3/5. In this case, the fraction is already in its simplest form, meaning the numerator and denominator have no common factors other than 1.
Therefore, 3 times 1/5 is 3/5.
Visual Representation: Making it Concrete
Let's visualize this using our pie example. If we have three pies, each cut into five equal slices, and we take one slice from each pie, we'll have a total of three slices. Since each pie has five slices, these three slices represent 3/5 of a whole pie.
Imagine you're sharing pizza with friends. You have three pizzas, and each is cut into five slices. If each person takes one slice from each pizza, how much pizza will they have? They'll have three out of five slices, or 3/5 of a pizza. This visual representation makes the concept of 3 x 1/5 = 3/5 more intuitive and easy to grasp.
Different Perspectives: Exploring Other Approaches
While the method above is the most efficient, it's valuable to consider other perspectives to solidify understanding:
-
Repeated Addition: As mentioned earlier, 3 x 1/5 can be understood as adding 1/5 three times: 1/5 + 1/5 + 1/5 = 3/5. This approach is particularly helpful for beginners as it directly connects multiplication to repeated addition.
-
Area Model: Imagine a rectangle representing a whole unit. Divide it into five equal vertical strips representing fifths. Now, shade three of these strips. This shaded area represents 3/5 of the whole rectangle. This visual method is excellent for visualizing fractions and multiplication.
Going Further: Multiplying Fractions with Fractions
Understanding 3 times 1/5 provides a foundation for tackling more complex fraction multiplication problems. When multiplying two fractions, the process is similar:
- Multiply the numerators: Multiply the top numbers together.
- Multiply the denominators: Multiply the bottom numbers together.
- Simplify the resulting fraction (if possible): Reduce the fraction to its simplest form by finding the greatest common divisor of the numerator and denominator and dividing both by it.
For example, to multiply 2/3 by 1/4, we would do: (2 * 1) / (3 * 4) = 2/12. This simplifies to 1/6 by dividing both numerator and denominator by 2.
Addressing Common Misconceptions
Several common misconceptions can arise when working with fractions:
-
Adding denominators when multiplying: A frequent mistake is adding the denominators instead of multiplying them. Remember, when multiplying fractions, we multiply the numerators and multiply the denominators separately.
-
Not simplifying fractions: Leaving the answer as an unsimplified fraction can obscure the true value. Always simplify the fraction to its lowest terms to make it easier to understand and compare with other fractions.
-
Confusing multiplication with addition: Remember that multiplying a fraction by a whole number means adding the fraction repeatedly, not simply combining the numbers in the fraction and the whole number.
Frequently Asked Questions (FAQ)
Q: Can I multiply fractions with different denominators?
A: Yes, absolutely. The process remains the same. Multiply the numerators together, multiply the denominators together, and then simplify the result.
Q: What if the resulting fraction is an improper fraction (numerator is larger than the denominator)?
A: An improper fraction is perfectly valid. However, it's often helpful to convert it to a mixed number (a whole number and a fraction). For example, 7/5 is an improper fraction that converts to the mixed number 1 2/5.
Q: Are there any online resources or tools that can help me practice fraction multiplication?
A: Many websites and educational apps offer interactive exercises and games to help you practice multiplying fractions. Search online for "fraction multiplication practice" to find numerous resources.
Q: How can I explain this concept to a young child?
A: Use visual aids like pizzas, cookies, or blocks to represent the fractions. Hands-on activities are incredibly effective in teaching children about fractions.
Conclusion: Mastering Fraction Multiplication
Mastering the concept of multiplying fractions, even seemingly simple ones like 3 times 1/5, builds a strong foundation for more advanced mathematical concepts. By understanding the process, visualizing the results, and addressing common misconceptions, you can confidently tackle fraction multiplication problems and appreciate the elegance of this fundamental mathematical operation. Remember to practice regularly to solidify your understanding and develop fluency. The more you work with fractions, the more comfortable and confident you’ll become. With consistent effort, you'll not only know the answer to "What is 3 times 1/5?" but also possess a deep understanding of the underlying principles.
Latest Posts
Latest Posts
-
5 To The First Power
Sep 15, 2025
-
Gcf Of 18 And 60
Sep 15, 2025
-
1 4 As Improper Fraction
Sep 15, 2025
-
What Is 1 In Fraction
Sep 15, 2025
-
Future Value Of One Table
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Times 1/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.