What Is 40 Of 49.99
saludintensiva
Sep 23, 2025 · 5 min read
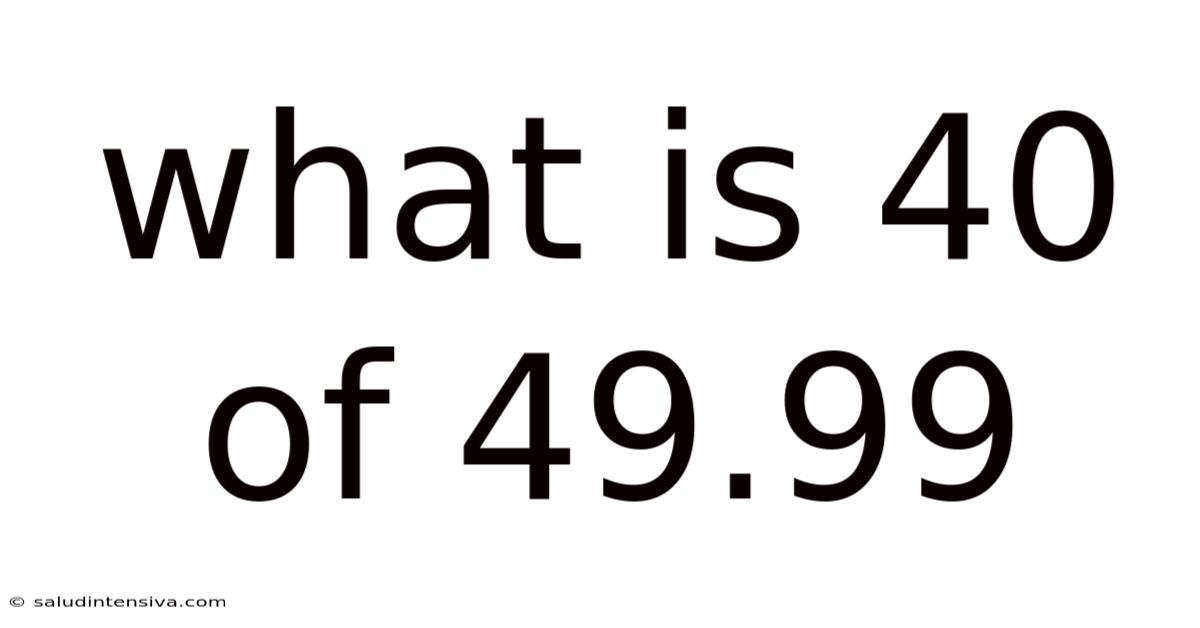
Table of Contents
What is 40% of 49.99? A Deep Dive into Percentages and Practical Applications
Finding 40% of 49.99 might seem like a simple calculation, but understanding the underlying principles of percentages unlocks a world of practical applications in everyday life, from budgeting and shopping to understanding financial reports and analyzing data. This article will not only show you how to calculate 40% of 49.99 but also delve into the broader concepts of percentages, providing you with the tools to confidently tackle similar problems in the future.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Understanding this fundamental definition is crucial. When we say "40%," we mean 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40.
This understanding forms the basis for calculating percentages. To find a percentage of a number, we essentially multiply the number by the percentage expressed as a decimal.
Calculating 40% of 49.99: The Step-by-Step Approach
There are several ways to calculate 40% of 49.99. Let's explore the most common methods:
Method 1: Using Decimal Multiplication
This is arguably the most straightforward method. We convert the percentage (40%) into its decimal equivalent (0.40) and then multiply it by the number (49.99):
49.99 * 0.40 = 19.996
Therefore, 40% of 49.99 is 19.996. In most practical scenarios, you would round this to 20.00.
Method 2: Using Fraction Multiplication
As mentioned earlier, 40% can also be represented as the fraction 40/100. We can use this fraction to calculate 40% of 49.99:
(40/100) * 49.99 = 0.4 * 49.99 = 19.996
This method yields the same result as the decimal multiplication method.
Method 3: Using Proportions
The concept of proportions provides another way to solve this problem. We set up a proportion where 'x' represents the unknown value (40% of 49.99):
40/100 = x/49.99
To solve for 'x', we cross-multiply:
100x = 40 * 49.99 100x = 1999.6 x = 1999.6 / 100 x = 19.996
Again, we arrive at the same answer: 19.996, which rounds to 20.00.
Practical Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving mathematical problems; it has wide-ranging practical applications in various aspects of life:
-
Shopping and Sales: Sales discounts are expressed as percentages. Calculating the discounted price of an item involves finding the percentage of the original price. For example, a 20% discount on a $100 item means you save $20 (20% of $100).
-
Financial Management: Percentages are fundamental to understanding interest rates, loan repayments, and investment returns. Calculating interest earned on savings accounts or interest payable on loans requires percentage calculations.
-
Tax Calculations: Sales tax, income tax, and other taxes are often expressed as percentages of the taxable amount. Accurately calculating taxes relies on understanding percentage calculations.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions and trends within datasets. For instance, expressing the percentage of people who prefer a certain product helps in market research and decision-making.
-
Tip Calculations: When dining out, calculating a tip based on a percentage of the bill is a common practice. For example, a 15% tip on a $50 meal is $7.50.
-
Grade Calculations: In educational settings, grades are often calculated as percentages of total points available.
-
Understanding Statistics: Percentage change is a key indicator in many areas like economics, where the change in stock prices or inflation are often expressed as percentages. For instance, if the stock price increases by 10%, it means the stock's value rose by 10% of its previous value.
Beyond the Basics: More Complex Percentage Problems
While finding 40% of 49.99 is a relatively simple calculation, the principles involved can be applied to more complex scenarios:
-
Finding the Original Price: If you know the discounted price and the percentage discount, you can work backward to find the original price.
-
Calculating Percentage Increase or Decrease: Determining the percentage change between two values requires understanding how to express the difference as a percentage of the original value.
-
Compound Interest: Compound interest calculations involve applying percentages repeatedly over time, leading to exponential growth (or decay).
-
Calculating Percentage Points: It's important to distinguish between percentage change and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly without a calculator?
A: For simple percentages like 10%, 20%, 25%, and 50%, you can use mental math techniques. For example, 10% is simply dividing the number by 10, 25% is dividing by 4, and 50% is dividing by 2. For other percentages, you might need to break them down into simpler fractions or use approximations.
Q: What if I need to calculate a percentage of a number that includes decimals?
A: The process remains the same. Convert the percentage to a decimal and multiply it by the number, including the decimal places.
Q: What are some common errors to avoid when calculating percentages?
A: Common errors include incorrectly converting percentages to decimals (e.g., using 40 instead of 0.40 for 40%), forgetting to multiply by the original number, and misinterpreting percentage increases/decreases versus percentage points.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a vital skill for navigating the complexities of everyday life and professional endeavors. From making informed financial decisions to analyzing data effectively, the ability to accurately calculate and interpret percentages unlocks a wealth of opportunities. While the calculation of 40% of 49.99 might seem trivial, the underlying concepts extend far beyond this simple example, equipping you with the knowledge to tackle more complex percentage-related problems with confidence and precision. Remember to practice regularly and explore different methods to solidify your understanding and build your proficiency. The more comfortable you become with percentages, the more empowered you'll be to make informed choices and achieve your goals.
Latest Posts
Latest Posts
-
Calculate Z Score In R
Sep 23, 2025
-
Powers Of Products And Quotients
Sep 23, 2025
-
30 Days From October 3rd
Sep 23, 2025
-
What Is The Aerobic Threshold
Sep 23, 2025
-
How To Find Arithmetic Density
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 49.99 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.