What Is 6/9 Equal To
saludintensiva
Sep 17, 2025 · 6 min read
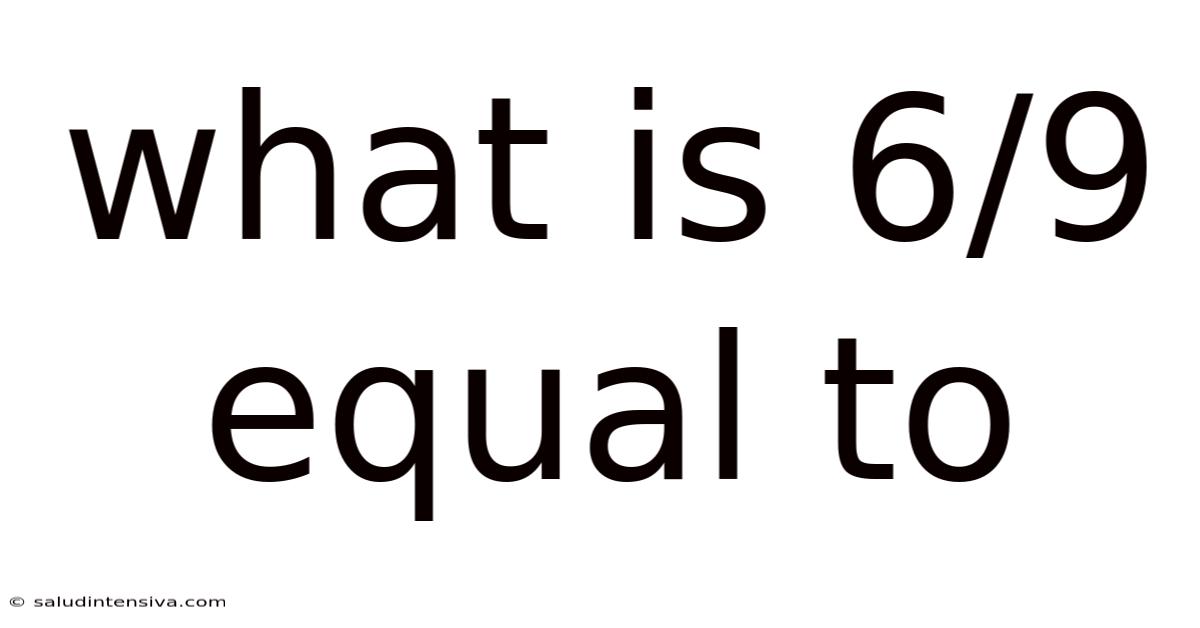
Table of Contents
What is 6/9 Equal To? Unpacking Fractions and Simplification
What is 6/9 equal to? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the immediate answer might seem straightforward, exploring this question allows us to delve into the principles of simplification, equivalent fractions, and the relationship between numerators and denominators. This article will provide a comprehensive explanation, suitable for learners of all levels, from elementary school students to those brushing up on their foundational math skills.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For instance, in the fraction 6/9, 9 represents the total number of equal parts, and 6 represents the number of parts we're interested in.
Understanding 6/9: The Initial Answer
The most basic answer to "What is 6/9 equal to?" is simply 6/9. This is a perfectly valid representation of the fraction. However, in mathematics, we often strive for the simplest form of a fraction. This simplified form represents the same value but uses smaller numbers, making it easier to understand and work with.
Simplifying Fractions: Finding the Greatest Common Factor (GCF)
Simplifying a fraction involves reducing it to its lowest terms. This is achieved by finding the greatest common factor (GCF) of the numerator and denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCF of 6 and 9, we can list the factors of each number:
- Factors of 6: 1, 2, 3, 6
- Factors of 9: 1, 3, 9
The largest number that appears in both lists is 3. Therefore, the GCF of 6 and 9 is 3.
Simplifying 6/9: Dividing by the GCF
Once we've found the GCF, we divide both the numerator and the denominator by that number. This process doesn't change the value of the fraction; it only changes its representation.
6 ÷ 3 = 2 9 ÷ 3 = 3
Therefore, the simplified form of 6/9 is 2/3.
Visual Representation of Equivalent Fractions
To further illustrate the equivalence of 6/9 and 2/3, let's consider a visual representation. Imagine a pizza cut into 9 equal slices. If you take 6 of those slices, you have 6/9 of the pizza. Now, imagine the same pizza cut into only 3 equal slices (larger slices). Taking 2 of these larger slices represents the same amount of pizza as taking 6 of the smaller slices. This visually demonstrates that 6/9 and 2/3 represent the same quantity.
Equivalent Fractions: Exploring Different Representations
The concept of equivalent fractions is crucial here. Equivalent fractions represent the same proportion or value, even though they have different numerators and denominators. We can generate equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example, multiplying both the numerator and denominator of 2/3 by 2 gives us 4/6, which is equivalent to 2/3 and 6/9. Similarly, multiplying by 3 gives 6/9, confirming our simplification.
Decimal and Percentage Equivalents
It's important to understand that fractions can also be expressed as decimals and percentages. To convert 6/9 (or its simplified form 2/3) to a decimal, we perform the division: 2 ÷ 3 ≈ 0.666... This is a repeating decimal.
To express it as a percentage, we multiply the decimal by 100: 0.666... × 100 ≈ 66.67%. Again, this is an approximation because the decimal is repeating.
Applications of Fractions in Real Life
Understanding fractions is vital in many aspects of daily life. Here are a few examples:
- Cooking: Recipes often involve fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Measurement: Measuring lengths, weights, and volumes frequently uses fractions (e.g., 3/4 inch, 1/2 kilogram).
- Finance: Dealing with money often involves fractions (e.g., 1/4 of a dollar is 25 cents).
- Data analysis: Representing proportions and ratios in data analysis commonly uses fractions.
Common Mistakes and Misconceptions
A common mistake is to only divide the numerator or the denominator by the GCF, instead of both. This results in an incorrect, unequal fraction. Always remember to divide both the numerator and the denominator by the GCF.
Another misconception is believing that simplifying a fraction changes its value. It doesn't. Simplifying only changes the way the fraction is represented, not its inherent value.
Advanced Concepts: Improper Fractions and Mixed Numbers
The fraction 6/9 is a proper fraction because the numerator (6) is smaller than the denominator (9). If the numerator is larger than or equal to the denominator, it's an improper fraction. Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction.
For example, the improper fraction 9/2 can be converted to the mixed number 4 1/2. This represents 4 whole units and an additional half unit.
Further Exploration: Working with Fractions
This understanding of 6/9 = 2/3 forms a foundation for more advanced concepts involving fractions. These include:
- Adding and subtracting fractions: Requires finding a common denominator.
- Multiplying and dividing fractions: Involves multiplying or inverting the second fraction and then multiplying numerators and denominators.
- Solving equations involving fractions: Requires applying algebraic principles.
Frequently Asked Questions (FAQ)
Q: Can I simplify 6/9 by dividing by 2?
A: No, you can't divide both the numerator and the denominator by 2, because 9 is not divisible by 2 without leaving a remainder. You must use the greatest common factor, which is 3.
Q: Is 2/3 the only simplified form of 6/9?
A: Yes, 2/3 is the simplest form because there are no common factors other than 1 between 2 and 3.
Q: What if I get a different answer when I simplify a fraction?
A: Double-check your calculations. Make sure you found the correct greatest common factor and divided both the numerator and denominator by that factor.
Conclusion: Mastering the Fundamentals of Fractions
Understanding what 6/9 is equal to—and, more importantly, how to simplify it to 2/3—is a crucial step in mastering fractions. This seemingly simple problem reveals the underlying principles of equivalent fractions, greatest common factors, and the importance of simplification. By grasping these concepts, you build a solid foundation for tackling more complex mathematical problems involving fractions, laying the groundwork for success in higher-level mathematics and beyond. Remember to practice regularly, and don't hesitate to explore further to solidify your understanding. The power of fractions extends far beyond the classroom, impacting countless aspects of our daily lives.
Latest Posts
Latest Posts
-
20 9 As A Mixed Number
Sep 17, 2025
-
160 M2 To Square Feet
Sep 17, 2025
-
What Is 80 Of 30000
Sep 17, 2025
-
The Difference Of Two Squares
Sep 17, 2025
-
1 1 7 As A Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 6/9 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.