What Is 9/12 Equal To
saludintensiva
Sep 15, 2025 · 6 min read
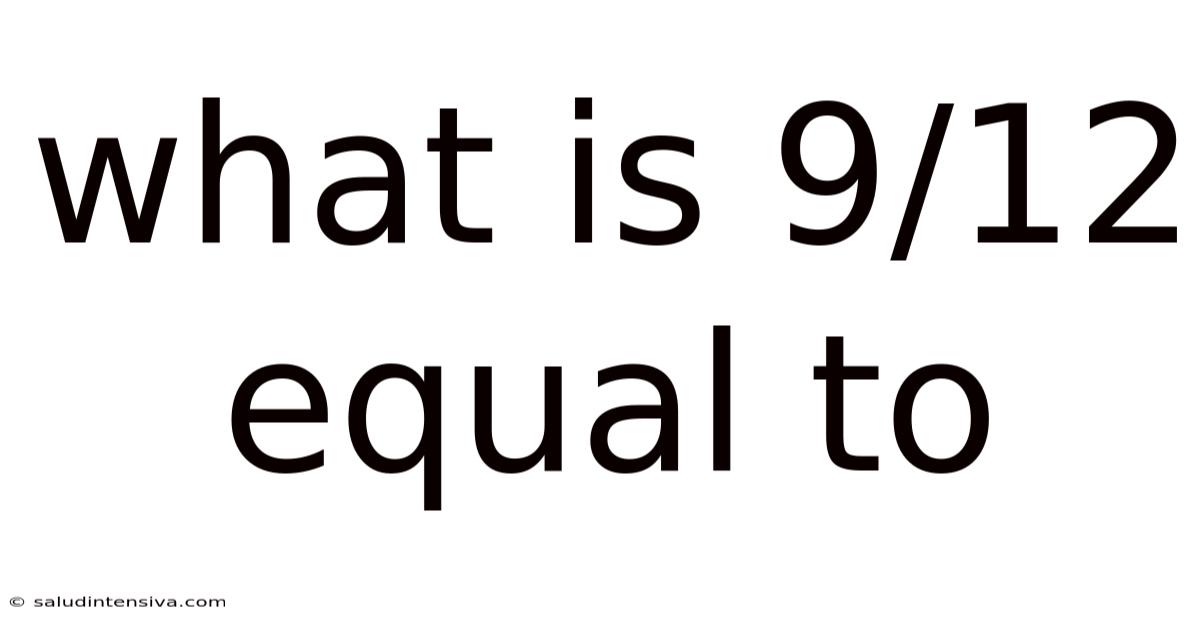
Table of Contents
What is 9/12 Equal To? A Comprehensive Exploration of Fraction Simplification and Equivalent Fractions
This article explores the seemingly simple question: what is 9/12 equal to? While the answer might seem immediately obvious to some, a deeper dive reveals fundamental concepts in mathematics, particularly concerning fractions, simplification, and equivalent fractions. This exploration will be beneficial for students learning fractions, as well as anyone seeking to refresh their understanding of these core mathematical principles. We will cover the basic calculation, delve into the concept of simplifying fractions, explore equivalent fractions, and address frequently asked questions.
Understanding Fractions: The Building Blocks
Before we tackle 9/12, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) signifies that the whole is divided into four equal parts.
Calculating 9/12: A Simple Approach
The most straightforward way to understand what 9/12 equals is to visualize it. Imagine a pizza cut into 12 equal slices. If you take 9 of those slices, you have 9/12 of the pizza. While this visually represents the fraction, it doesn't provide a simplified form.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This process is also known as expressing the fraction in lowest terms. To simplify 9/12, we need to find the greatest common divisor (GCD) of 9 and 12. The GCD is the largest number that divides both 9 and 12 without leaving a remainder.
The factors of 9 are 1, 3, and 9. The factors of 12 are 1, 2, 3, 4, 6, and 12.
The greatest common factor of 9 and 12 is 3. We then divide both the numerator and the denominator by the GCD:
9 ÷ 3 = 3 12 ÷ 3 = 4
Therefore, 9/12 simplified is 3/4. This means that 9/12 and 3/4 represent the same value; they are equivalent fractions.
Equivalent Fractions: Different Representations, Same Value
Equivalent fractions are fractions that represent the same proportion or value, even though they have different numerators and denominators. We can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example:
- Multiplying: 3/4 x 2/2 = 6/8. Both 3/4 and 6/8 represent the same value (three-quarters).
- Dividing: 6/8 ÷ 2/2 = 3/4. Reducing 6/8 to its lowest terms gives us 3/4.
This highlights the importance of simplifying fractions. While 9/12, 6/8, and 3/4 are all equivalent fractions, 3/4 is the most concise and easily understood representation.
Visualizing Equivalent Fractions
Visual aids can significantly improve understanding. Imagine a square divided into 12 equal parts. Shading 9 of those parts represents 9/12. Now, imagine grouping those 12 parts into four larger groups of 3 parts each. Shading 3 of those four larger groups still represents the same area – three-quarters of the square. This visual demonstration clearly shows the equivalence of 9/12 and 3/4.
The Importance of Simplification in Mathematics
Simplifying fractions isn't just about making things look neater. It's crucial for several reasons:
- Clarity and Understanding: Simplified fractions are easier to understand and compare. It's much easier to grasp the concept of 3/4 than 9/12, especially when dealing with more complex calculations.
- Efficiency in Calculations: Working with simplified fractions makes calculations quicker and less prone to errors. Imagine adding 9/12 and 3/12 – it's simpler to add 3/4 and 1/4.
- Foundation for Advanced Concepts: Simplifying fractions is a foundational skill necessary for understanding more advanced mathematical concepts like ratios, proportions, and algebraic equations.
Real-World Applications of Fraction Simplification
The ability to simplify fractions isn't confined to the classroom. It has numerous practical applications in daily life:
- Cooking and Baking: Recipes often use fractions. Simplifying fractions can make it easier to measure ingredients accurately.
- Construction and Engineering: Precise measurements are essential. Simplifying fractions helps in calculations involving lengths, areas, and volumes.
- Finance and Budgeting: Understanding and simplifying fractions is crucial for managing personal finances, understanding percentages, and calculating interest rates.
Beyond Simplification: Decimal and Percentage Equivalents
While 3/4 is the simplest fraction equivalent to 9/12, we can also express this value as a decimal or a percentage:
- Decimal: To convert a fraction to a decimal, divide the numerator by the denominator: 3 ÷ 4 = 0.75
- Percentage: To convert a fraction to a percentage, multiply the decimal by 100: 0.75 x 100 = 75%
Therefore, 9/12 is equal to 3/4, 0.75, and 75%. All three representations convey the same value, but their context of use might differ. Percentages are useful for expressing proportions, while decimals are often preferred in calculations involving computers or other technologies.
Frequently Asked Questions (FAQ)
Q: Can I simplify 9/12 by dividing by any number?
A: No, you must divide both the numerator and denominator by their greatest common divisor (GCD) to reach the simplest form. Dividing by a smaller common factor will result in a simplified fraction, but not the simplest one.
Q: What if the numerator and denominator have no common factors other than 1?
A: If the greatest common divisor is 1, the fraction is already in its simplest form. For example, 5/7 is already in its simplest form.
Q: Are there other ways to simplify fractions besides finding the GCD?
A: Yes, you can simplify fractions by repeatedly dividing both the numerator and denominator by common factors until no further simplification is possible. However, finding the GCD is the most efficient method.
Q: Why is simplifying fractions important in algebra?
A: Simplifying fractions is crucial in algebra because it simplifies equations and expressions, making them easier to solve and manipulate. It helps to avoid unnecessary complexity and reduces the chance of errors.
Q: How can I improve my skills in simplifying fractions?
A: Practice is key. Work through numerous examples, starting with simple fractions and gradually progressing to more complex ones. Use visual aids and understand the concept of GCD. Utilize online resources and educational materials for additional practice and clarification.
Conclusion: Mastering the Fundamentals of Fractions
Understanding what 9/12 equals goes beyond a simple calculation. It's about grasping the fundamental concepts of fractions, simplification, equivalent fractions, and their practical applications. Mastering these concepts forms a crucial foundation for further mathematical learning and success in various fields. By understanding simplification, we can efficiently manage numbers, represent proportions clearly, and pave the way for more advanced mathematical explorations. Remember, the journey to mathematical proficiency is built upon a strong understanding of basic principles, and the seemingly simple question of 9/12 serves as a perfect example of this important truth. Keep practicing, and you will gradually develop a firm grasp of these essential concepts.
Latest Posts
Latest Posts
-
What Is 3 4kg In Pounds
Sep 15, 2025
-
Square Root Of 1 2
Sep 15, 2025
-
Is 9 Prime Or Composite
Sep 15, 2025
-
15 20 As A Percent
Sep 15, 2025
-
All The Factors Of 24
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 9/12 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.