What Is Equivalent To 2/8
saludintensiva
Sep 18, 2025 · 5 min read
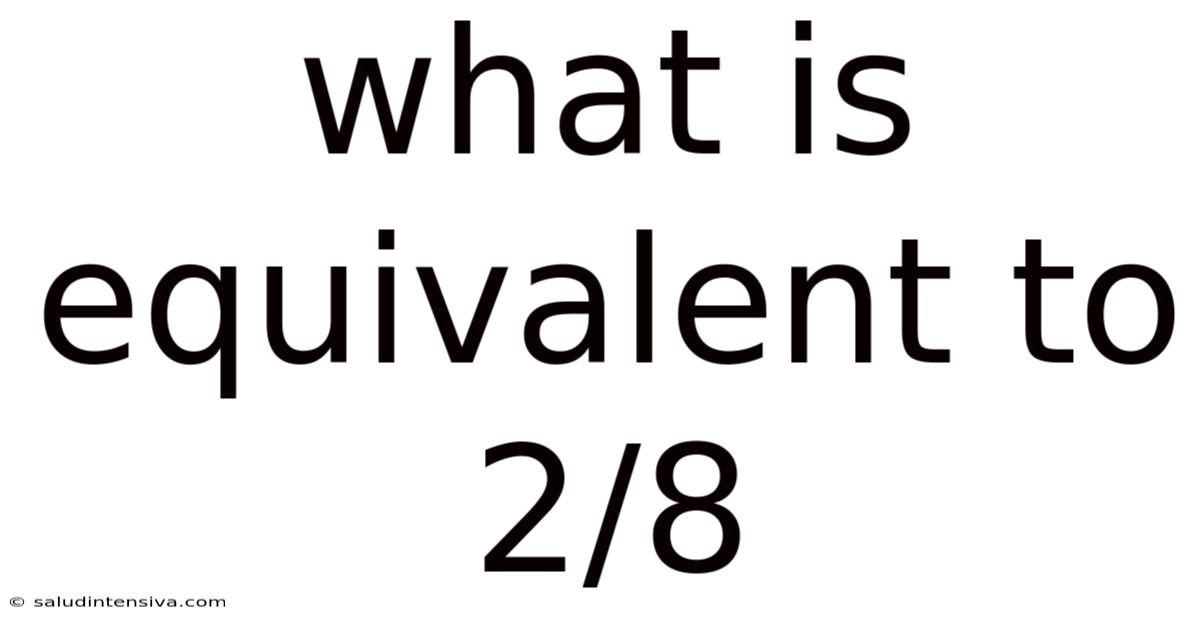
Table of Contents
What is Equivalent to 2/8? Unlocking the World of Fractions
Understanding fractions is a fundamental building block in mathematics, crucial for everything from baking a cake to calculating complex engineering projects. This article dives deep into the concept of equivalent fractions, using the example of 2/8 to illustrate the principles and demonstrate how to find and simplify fractions. We’ll explore various methods, address common misconceptions, and provide plenty of examples to solidify your understanding. By the end, you'll not only know what's equivalent to 2/8 but also possess a robust understanding of fraction equivalence.
Understanding Fractions: A Quick Refresher
Before we tackle the equivalence of 2/8, let's briefly review the components of a fraction. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number indicates how many parts we have. In the fraction 2/8, the numerator is 2.
- Denominator: The bottom number indicates how many equal parts the whole is divided into. In the fraction 2/8, the denominator is 8.
Therefore, 2/8 represents 2 out of 8 equal parts of a whole.
Finding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same proportion or value, even though they look different. Think of it like having different sized pieces of a pizza that still add up to the same amount. To find an equivalent fraction, we apply the fundamental principle: multiplying or dividing both the numerator and the denominator by the same non-zero number will not change the fraction's value.
Methods for Finding Equivalents to 2/8
Let's explore several approaches to find fractions equivalent to 2/8:
1. Simplifying Fractions (Finding the Simplest Form):
This is arguably the most important method. Simplifying, or reducing, a fraction means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This is also known as expressing the fraction in its lowest terms.
To simplify 2/8, we find the greatest common divisor (GCD) of the numerator (2) and the denominator (8). The GCD of 2 and 8 is 2. We then divide both the numerator and the denominator by the GCD:
2 ÷ 2 = 1 8 ÷ 2 = 4
Therefore, the simplest form of 2/8 is 1/4. This means 2/8 and 1/4 represent the same proportion.
2. Multiplying the Numerator and Denominator:
We can create numerous equivalent fractions by multiplying both the numerator and the denominator by the same number. Let's try a few examples:
- Multiplying by 2: (2 x 2) / (8 x 2) = 4/16
- Multiplying by 3: (2 x 3) / (8 x 3) = 6/24
- Multiplying by 4: (2 x 4) / (8 x 4) = 8/32
- Multiplying by 5: (2 x 5) / (8 x 5) = 10/40
All of these fractions – 4/16, 6/24, 8/32, and 10/40 – are equivalent to 2/8 and, consequently, also equivalent to 1/4.
3. Using Visual Representations:
Visual aids can significantly improve understanding. Imagine a pizza cut into 8 slices. If you take 2 slices, you've taken 2/8 of the pizza. Now, imagine the same pizza cut into 4 slices instead. Taking one of those larger slices is the same as taking 2 of the smaller slices – it's 1/4 of the pizza. This visual representation clearly demonstrates the equivalence between 2/8 and 1/4.
Why Simplifying Fractions is Important
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and compare. It's much simpler to grasp the meaning of 1/4 than 8/32, even though they represent the same value.
- Efficiency: Simplified fractions make calculations more efficient. Working with smaller numbers is less prone to errors and requires less effort.
- Standardization: Presenting fractions in their simplest form is a standard practice in mathematics, ensuring consistency and clear communication.
Beyond 2/8: Generalizing the Concept of Equivalent Fractions
The methods used to find equivalent fractions for 2/8 apply to any fraction. The core principle remains consistent: multiplying or dividing both the numerator and the denominator by the same non-zero number results in an equivalent fraction.
Common Mistakes and Misconceptions
- Only multiplying the numerator or denominator: A common mistake is to only multiply the numerator or the denominator, which drastically changes the value of the fraction. Remember, both must be multiplied (or divided) by the same number.
- Incorrect simplification: Errors can occur when trying to simplify a fraction by not finding the greatest common divisor. Always look for the largest number that divides both the numerator and the denominator evenly.
- Confusion with addition and subtraction: Remember that finding equivalent fractions is different from adding or subtracting fractions. Equivalent fractions maintain the same value; adding or subtracting changes the value.
Frequently Asked Questions (FAQ)
Q: Is there an infinite number of equivalent fractions for 2/8?
A: Yes. Since you can multiply the numerator and denominator by any non-zero number, there's an infinite number of equivalent fractions.
Q: How do I know if two fractions are equivalent?
A: Two fractions are equivalent if you can simplify both to the same simplest form, or if you can obtain one from the other by multiplying (or dividing) both the numerator and the denominator by the same non-zero number.
Q: What is the importance of equivalent fractions in real-life applications?
A: Equivalent fractions are used extensively in various real-life situations, including cooking (measuring ingredients), construction (measuring materials), and finance (calculating proportions and percentages).
Q: Why can't we multiply or divide by zero when finding equivalent fractions?
A: Division by zero is undefined in mathematics. Multiplying by zero would always result in a fraction equal to zero, regardless of the original fraction's value.
Conclusion
Understanding equivalent fractions is paramount for mastering fundamental mathematical concepts. This article demonstrated various methods to find equivalents for 2/8, highlighting the importance of simplification and clarifying common misconceptions. Remember, the core principle is always to maintain the proportional relationship between the numerator and the denominator. By consistently applying these techniques and principles, you can confidently work with fractions in any context, from simple arithmetic to more complex mathematical applications. The ability to identify and work with equivalent fractions is a key skill that will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Kg M3 To G Ml
Sep 18, 2025
-
What Is 4 20 Simplified
Sep 18, 2025
-
12 25 In Decimal Form
Sep 18, 2025
-
1 2 To The 2nd Power
Sep 18, 2025
-
Multiplication Of Rational Numbers Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 2/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.