What Is Equivalent To 3/6
saludintensiva
Sep 11, 2025 · 6 min read
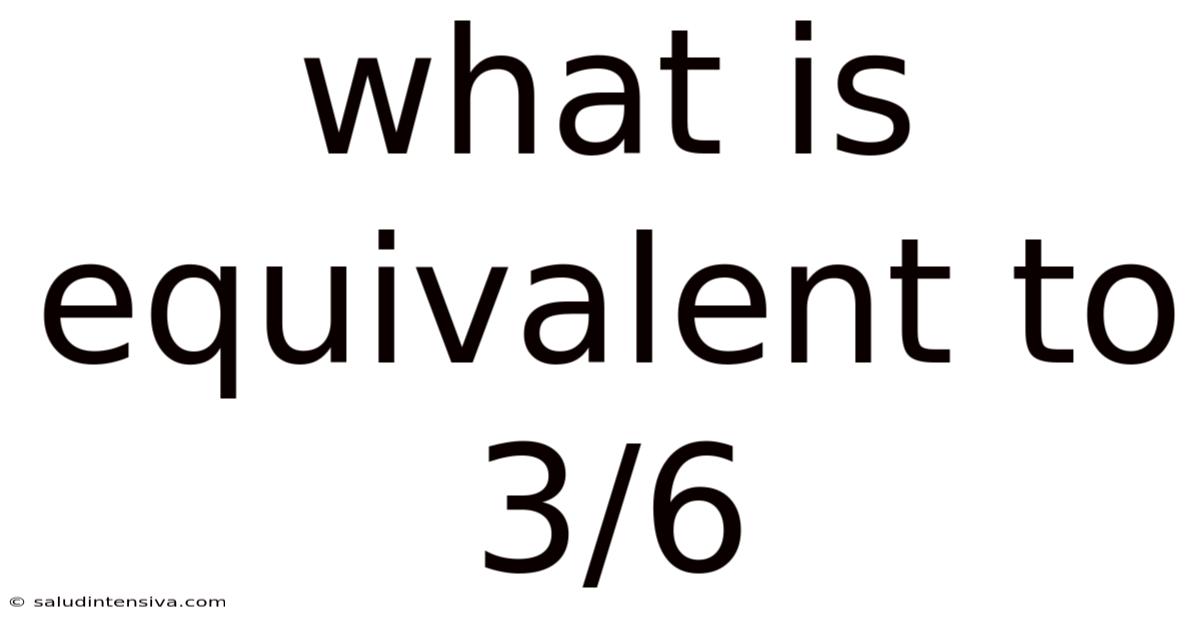
Table of Contents
What is Equivalent to 3/6? Unlocking the World of Fractions and Equivalence
Understanding fractions is a cornerstone of mathematical literacy. This seemingly simple question – "What is equivalent to 3/6?" – opens the door to a deeper understanding of fundamental mathematical concepts like equivalence, simplification, and the relationship between numerators and denominators. This article will explore not just the answer, but the underlying principles, providing a comprehensive guide for learners of all levels. We'll delve into various methods for finding equivalent fractions, explore the importance of simplification, and address frequently asked questions about fraction equivalence.
Introduction: The Meaning of Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Think of slicing a pizza: 3 out of 6 slices (3/6) is exactly the same as having 1 out of 2 slices (1/2). Both represent half the pizza. The key is that the ratio between the numerator (the top number) and the denominator (the bottom number) remains constant. This article will explain how to identify and calculate these equivalent fractions, emphasizing the importance of understanding the underlying mathematical concepts.
Finding Equivalent Fractions: The Fundamental Methods
There are several ways to determine a fraction equivalent to 3/6. Let's explore the most common methods:
1. Simplifying Fractions: This is the most direct method. Simplifying a fraction means reducing it to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 3 and 6 is 3. Therefore:
3/6 = (3 ÷ 3) / (6 ÷ 3) = 1/2
This shows that 3/6 is equivalent to 1/2. It's the simplest form of the fraction, meaning there are no common factors (other than 1) between the numerator and the denominator.
2. Multiplying the Numerator and Denominator by the Same Number: This method allows us to generate infinitely many equivalent fractions. We can multiply both the numerator and the denominator of 3/6 by any non-zero integer. For example:
- Multiplying by 2: (3 x 2) / (6 x 2) = 6/12
- Multiplying by 3: (3 x 3) / (6 x 3) = 9/18
- Multiplying by 4: (3 x 4) / (6 x 4) = 12/24
All these fractions – 6/12, 9/18, 12/24 – are equivalent to 3/6 and, consequently, to 1/2. The key is maintaining the ratio; whatever you multiply the numerator by, you must also multiply the denominator by the same number.
3. Using Visual Representations: Visual aids can significantly improve understanding, particularly for beginners. Imagine a rectangular bar divided into six equal parts. Shading three of those parts visually represents 3/6. Now, imagine dividing the same bar in half. Shading one of the two halves represents 1/2. The shaded area remains the same; hence, 3/6 and 1/2 are equivalent. Similar visualizations can be used with circles, pies, or any other shapes divided into equal parts.
The Importance of Simplifying Fractions
Simplifying fractions is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and compare. It's much simpler to work with 1/2 than 6/12, 9/18, or 12/24.
-
Efficiency: Simplifying reduces the complexity of calculations. In more complex mathematical operations, working with simplified fractions significantly reduces the risk of errors and simplifies the process.
-
Standardization: In mathematics, it's standard practice to present fractions in their simplest form. This ensures consistency and facilitates communication.
-
Problem Solving: Simplifying fractions is often a necessary step in solving more complex problems involving fractions, such as adding, subtracting, multiplying, and dividing fractions.
Beyond the Basics: Exploring Fraction Equivalence in Deeper Detail
The concept of equivalent fractions is fundamental to many advanced mathematical concepts. Let's delve into some more nuanced aspects:
1. Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾). Equivalent fractions can also exist between improper fractions and mixed numbers. For instance, 7/4 is equivalent to 1 ¾.
2. Decimal Equivalents: Fractions can be converted to decimals and vice-versa. The decimal equivalent of 3/6 (or 1/2) is 0.5. Understanding this connection strengthens your overall grasp of numerical representation.
3. Ratio and Proportion: Equivalent fractions are directly related to the concept of ratio and proportion. A ratio compares two quantities, and a proportion states that two ratios are equal. The equivalence of 3/6 and 1/2 can be expressed as a proportion: 3/6 = 1/2.
4. Applications in Real Life: Understanding equivalent fractions has countless real-world applications. From cooking (following recipes that require fractional measurements) to construction (calculating proportions for building materials), the ability to work with and manipulate fractions is invaluable.
Frequently Asked Questions (FAQ)
Q1: Are there infinitely many equivalent fractions to 3/6?
A1: Yes, there are infinitely many equivalent fractions to 3/6 (or 1/2). You can generate them by multiplying the numerator and denominator by any non-zero integer.
Q2: How do I find the simplest form of a fraction?
A2: To find the simplest form, divide both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder.
Q3: Why is simplifying fractions important?
A3: Simplifying makes fractions easier to understand, compare, and work with in calculations, leading to greater efficiency and reduced error.
Q4: Can I use a calculator to find equivalent fractions?
A4: While calculators can help with the division involved in simplifying fractions, they don't directly find equivalent fractions. Understanding the underlying mathematical principles is essential.
Q5: What if I have a fraction with a large numerator and denominator? How do I simplify it?
A5: For large numbers, finding the GCD might require a systematic approach like prime factorization. Break down both the numerator and the denominator into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
Conclusion: Mastering the Art of Fraction Equivalence
The seemingly simple question of what is equivalent to 3/6 leads us on a journey into the fascinating world of fractions and their properties. This article has not only provided the answer (1/2, and infinitely many others) but also explored the underlying principles of fraction equivalence, emphasizing the significance of simplification and the broad applications of this fundamental concept. Understanding equivalent fractions is not just about manipulating numbers; it's about developing a deeper mathematical intuition and a solid foundation for tackling more advanced mathematical concepts. Mastering this skill will undoubtedly enhance your problem-solving abilities and open doors to a wider range of mathematical explorations. Remember to practice regularly, utilize visual aids, and always strive to understand the 'why' behind the 'how' to truly master this essential mathematical concept.
Latest Posts
Latest Posts
-
21 50 As A Decimal
Sep 11, 2025
-
Sum And Difference Formula Calculator
Sep 11, 2025
-
45 Percent As A Decimal
Sep 11, 2025
-
700 Square Feet In Feet
Sep 11, 2025
-
What Is 6 16 Simplified
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 3/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.