What Is Half Of 28
saludintensiva
Sep 13, 2025 · 5 min read
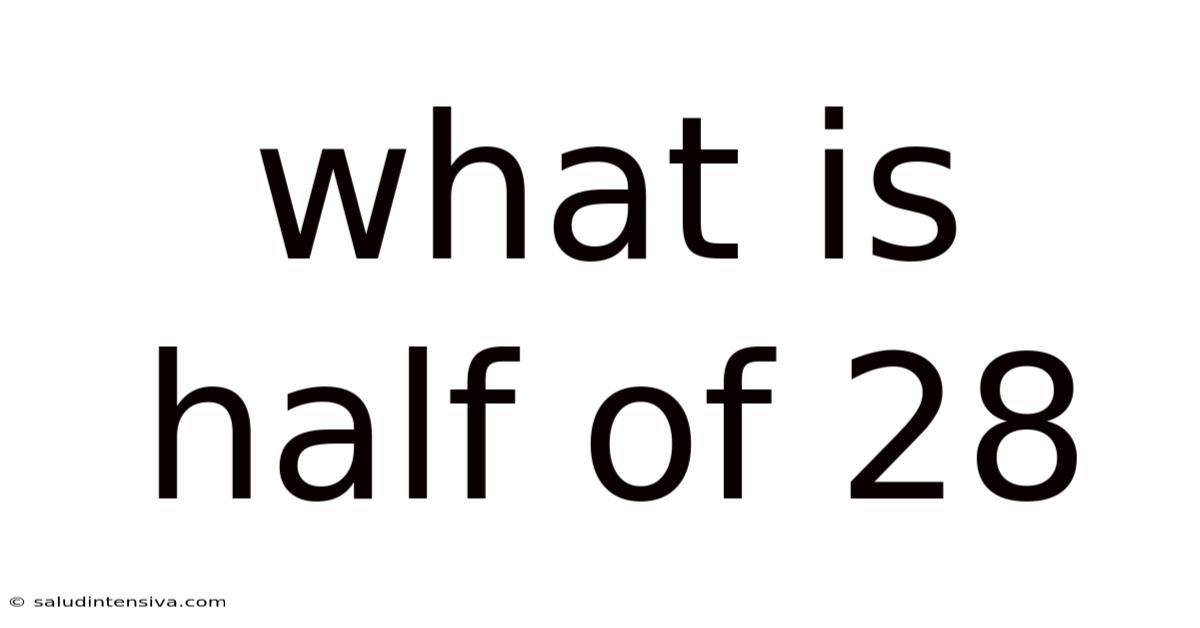
Table of Contents
What is Half of 28? A Deep Dive into Division and Fractions
Finding half of a number is a fundamental concept in mathematics, crucial for understanding fractions, percentages, and more advanced mathematical operations. This seemingly simple question, "What is half of 28?", provides a springboard to explore a range of mathematical ideas and their practical applications. This article will not only answer the question directly but also delve into the underlying principles, offering a comprehensive understanding of division and its relationship to fractions.
Understanding Division: The Foundation of Finding Half
Before we tackle finding half of 28, let's solidify our understanding of division. Division is essentially the process of splitting a quantity into equal parts. It's the inverse operation of multiplication; if you multiply a number by another, division undoes that process. For instance, 4 multiplied by 5 equals 20 (4 x 5 = 20); conversely, dividing 20 by 5 equals 4 (20 / 5 = 4).
Finding half of a number is a specific case of division. "Half" represents the fraction 1/2, meaning we're dividing the number into two equal parts. Therefore, finding half of 28 is equivalent to dividing 28 by 2.
Calculating Half of 28: The Solution
The simplest way to find half of 28 is through direct division:
28 / 2 = 14
Therefore, half of 28 is 14.
This simple calculation is the foundation upon which many more complex mathematical problems are built. Understanding this basic principle is vital for success in higher-level mathematics.
Fractions and Their Representation: Visualizing Half
The concept of "half" is intrinsically linked to fractions. A fraction represents a part of a whole. The fraction 1/2 signifies one part out of two equal parts. Visualizing this concept helps solidify the understanding. Imagine a pizza cut into two equal slices. One slice represents 1/2 of the whole pizza.
We can represent half of 28 using fractions:
(1/2) * 28 = 14
This illustrates that multiplying a number by 1/2 is equivalent to dividing it by 2. This interchangeability is a cornerstone of fractional arithmetic.
Extending the Concept: Finding Other Fractions of 28
Understanding how to find half of 28 allows us to expand our understanding and calculate other fractions of 28. For example:
- One-quarter (1/4) of 28: This involves dividing 28 by 4. 28 / 4 = 7. Therefore, one-quarter of 28 is 7.
- One-third (1/3) of 28: This involves dividing 28 by 3. 28 / 3 = 9 with a remainder of 1. This means that one-third of 28 is approximately 9.333... This introduces the concept of decimal representation of fractions.
- Three-quarters (3/4) of 28: This can be calculated in two ways: (a) find one-quarter (7) and multiply by 3 (7 x 3 = 21), or (b) multiply 28 by 3/4 (28 x (3/4) = 21). Therefore, three-quarters of 28 is 21.
These examples demonstrate the versatility of the fundamental concept of division and its application to finding fractions of a whole number.
Real-World Applications: Half in Everyday Life
The concept of finding half is far from an abstract mathematical exercise; it has numerous practical applications in our daily lives:
- Sharing: If you have 28 cookies and want to share them equally between two friends, you would give each friend 14 cookies (half of 28).
- Cooking: Many recipes require halving or doubling ingredients. If a recipe calls for 28 grams of flour, halving it would require 14 grams.
- Measurements: Converting units often involves finding fractions. For instance, converting inches to feet might require finding half or other fractions of a larger unit.
- Money: Dividing money equally among individuals or calculating discounts often involves finding halves or other fractions of a total amount.
- Geometry: Finding the midpoint of a line segment involves dividing the length of the segment in half.
These are just a few examples illustrating the ubiquitous nature of this seemingly simple mathematical concept.
Decimals and Percentages: Expressing Half in Different Forms
While the fraction 1/2 represents half, we can also express half using decimals and percentages:
- Decimal: 1/2 is equivalent to 0.5.
- Percentage: 1/2 is equivalent to 50%.
Understanding these different representations allows for flexibility in various mathematical contexts and problem-solving scenarios.
Beyond the Basics: Advanced Concepts Related to Division
While finding half of 28 is a straightforward calculation, it serves as a stepping stone to more complex mathematical concepts:
- Ratio and Proportion: The concept of "half" is directly related to ratios and proportions. A ratio of 1:2 signifies one part to two equal parts, reflecting the essence of finding half.
- Algebra: Solving algebraic equations often involves division and fractions. Understanding the fundamental concept of finding half is essential for mastering more advanced algebraic manipulations.
- Calculus: Calculus involves concepts like limits and derivatives, both of which build upon a strong understanding of basic arithmetic, including division.
- Statistics: Statistical analysis often involves calculating averages and proportions, which depend heavily on the ability to divide and understand fractions.
Frequently Asked Questions (FAQ)
Q: What is the opposite of finding half of a number?
A: The opposite of finding half (dividing by 2) is doubling (multiplying by 2).
Q: Can you find half of any number?
A: Yes, you can find half of any number, although for some numbers, the result will be a fraction or a decimal.
Q: What if I want to find more than half of 28?
A: You would multiply 28 by the fraction representing the desired portion. For example, to find three-quarters (3/4) of 28, you would calculate (3/4) * 28 = 21.
Q: Why is understanding "half" important in mathematics?
A: Understanding "half" is foundational to grasping fractions, division, percentages, and many advanced mathematical concepts. It's a key building block for more complex problem-solving.
Conclusion: The Significance of a Simple Calculation
The seemingly simple question, "What is half of 28?", opens a door to a world of mathematical concepts and practical applications. From the fundamentals of division and fractions to more advanced concepts like ratios, proportions, and algebraic manipulation, understanding how to find half of a number is a vital stepping stone in mathematical development. Mastering this basic skill provides a solid foundation for tackling more complex challenges and navigating the world of numbers with confidence and ease. This understanding is not just about getting the answer (14); it's about appreciating the underlying principles and their far-reaching implications in various aspects of life.
Latest Posts
Latest Posts
-
23 6 As A Decimal
Sep 13, 2025
-
What Is 4 5 In Fraction
Sep 13, 2025
-
55 Percent As A Decimal
Sep 13, 2025
-
Gcf Of 35 And 45
Sep 13, 2025
-
Whats 150 Minutes In Hours
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.