What Is Half Of 4/3
saludintensiva
Sep 14, 2025 · 5 min read
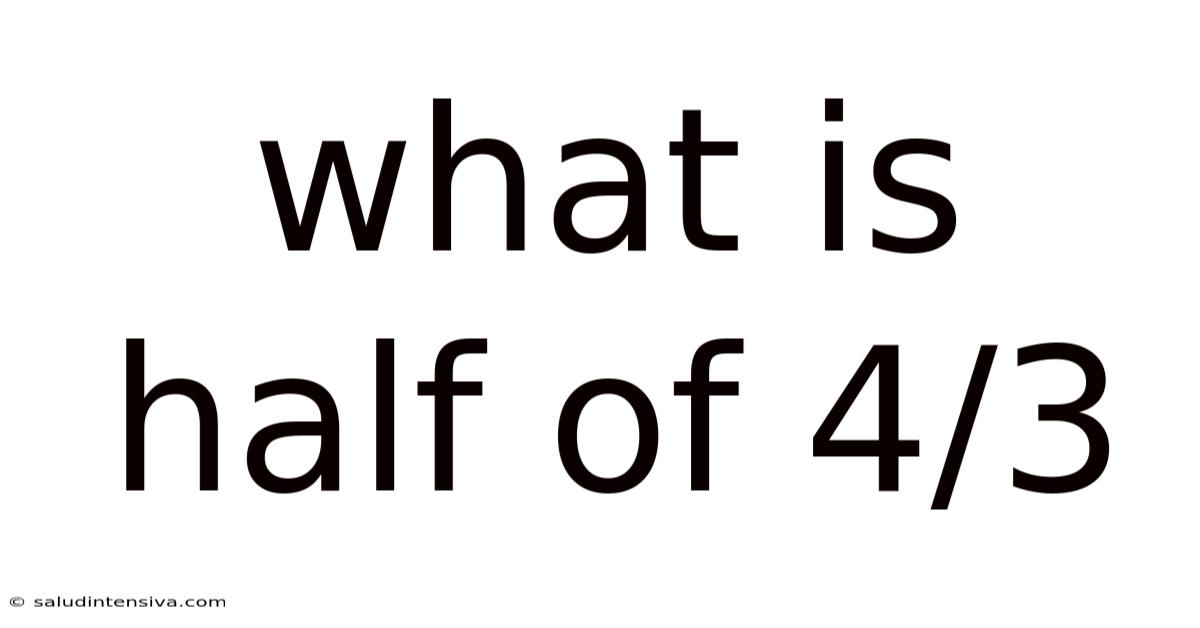
Table of Contents
What is Half of 4/3? A Deep Dive into Fractions and Division
Finding half of 4/3 might seem like a simple arithmetic problem, but it's a fantastic opportunity to explore fundamental concepts in mathematics, particularly fractions and division. This article will not only provide the answer but also delve into the underlying principles, explaining the process step-by-step and addressing common misconceptions. We'll even explore some real-world applications to solidify your understanding. Understanding fractions is crucial for various aspects of life, from baking to construction to advanced scientific calculations. This comprehensive guide will equip you with the knowledge and confidence to tackle similar problems with ease.
Understanding Fractions: The Building Blocks
Before we jump into finding half of 4/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 4/3, 4 is the numerator and 3 is the denominator. This means we have 4 parts out of a total of 3 equal parts. Notice that this is an improper fraction because the numerator is larger than the denominator. This indicates we have more than one whole.
Converting Improper Fractions to Mixed Numbers
Improper fractions are often converted to mixed numbers for easier understanding and interpretation. A mixed number combines a whole number and a proper fraction. To convert 4/3 to a mixed number, we perform a simple division:
4 ÷ 3 = 1 with a remainder of 1.
This means 4/3 is equivalent to 1 and 1/3. This representation clearly shows that we have one whole and one-third of another.
Finding Half: Division and Multiplication
Now, let's tackle the core question: what is half of 4/3? Finding half of something is the same as dividing it by 2. There are two main ways to approach this calculation:
Method 1: Dividing the Fraction Directly
To find half of 4/3, we can divide the fraction by 2. Remember that dividing by a whole number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2. Therefore:
(4/3) ÷ 2 = (4/3) × (1/2) = 4/6
This result, 4/6, can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2:
4/6 = (4 ÷ 2) / (6 ÷ 2) = 2/3
Therefore, half of 4/3 is 2/3.
Method 2: Dividing the Mixed Number
Alternatively, we can first convert 4/3 to a mixed number (1 1/3) and then find half. This can be done in two steps:
- Find half of the whole number: Half of 1 is 1/2.
- Find half of the fractional part: Half of 1/3 is (1/3) × (1/2) = 1/6.
Adding these two halves together, we get:
1/2 + 1/6 = 3/6 + 1/6 = 4/6 = 2/3
Again, we arrive at the same simplified answer: 2/3.
Visual Representation: Understanding the Concept
Imagine a pizza cut into three equal slices. 4/3 of a pizza means you have four of these slices. To find half, you would simply take half of those four slices, leaving you with two slices. Since the pizza was originally cut into three slices, you now have 2/3 of the pizza. This visual representation helps solidify the concept and makes the abstract calculation more concrete.
Explanation with Different Types of Fractions
Let's extend this concept to other types of fractions. Consider finding half of other fractions:
-
Half of 1/2: (1/2) ÷ 2 = (1/2) × (1/2) = 1/4. Half of half a pizza is a quarter of a pizza.
-
Half of 3/4: (3/4) ÷ 2 = (3/4) × (1/2) = 3/8. Half of three-quarters is three-eighths.
-
Half of 2: 2 ÷ 2 = 1. Half of two whole units is one whole unit.
These examples demonstrate the consistent application of the division principle: dividing by 2 is equivalent to multiplying by 1/2.
Real-World Applications
The concept of finding a fraction of a fraction is prevalent in various real-world scenarios:
-
Cooking and Baking: Recipes often require you to use a fraction of a given ingredient. For example, a recipe might call for half of 2/3 cup of sugar.
-
Construction and Measurement: Precise measurements in construction frequently involve fractions and their divisions.
-
Financial Calculations: Calculating percentages, interest rates, and profit margins involves working with fractions.
-
Data Analysis: Statistical analysis often uses fractions to represent proportions and probabilities.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, you can. Most calculators can handle fraction calculations. However, understanding the underlying principles is crucial for applying these concepts in more complex scenarios.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most concise form, representing the same value with smaller numbers.
Q: What if the fraction was a larger, more complex number?
A: The same principles apply. Convert to a mixed number if it helps, then divide by 2 (or multiply by 1/2). Simplification might require finding the greatest common divisor (GCD) of the numerator and denominator.
Q: What if I needed to find a third, or a quarter, of a fraction?
A: Instead of dividing by 2, you would divide by 3 or 4, respectively. This is the same as multiplying by 1/3 or 1/4.
Conclusion
Finding half of 4/3, which simplifies to 2/3, might seem straightforward at first glance. However, exploring the underlying concepts of fractions, improper fractions, mixed numbers, division, and simplification enhances your understanding of fundamental mathematical principles. This knowledge extends beyond simple arithmetic; it's the bedrock for more advanced mathematical concepts and real-world applications. Remember to practice regularly to solidify your understanding and build confidence in tackling similar problems. Mastering fractions is a key stepping stone to success in various academic and practical pursuits.
Latest Posts
Latest Posts
-
5 Feet And 3 Inches
Sep 14, 2025
-
Gcf Of 24 And 20
Sep 14, 2025
-
What Is 15 Of 9
Sep 14, 2025
-
75 Degree Celsius To Fahrenheit
Sep 14, 2025
-
19 30 In Military Time
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 4/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.