What Is Half Of 54
saludintensiva
Sep 18, 2025 · 5 min read
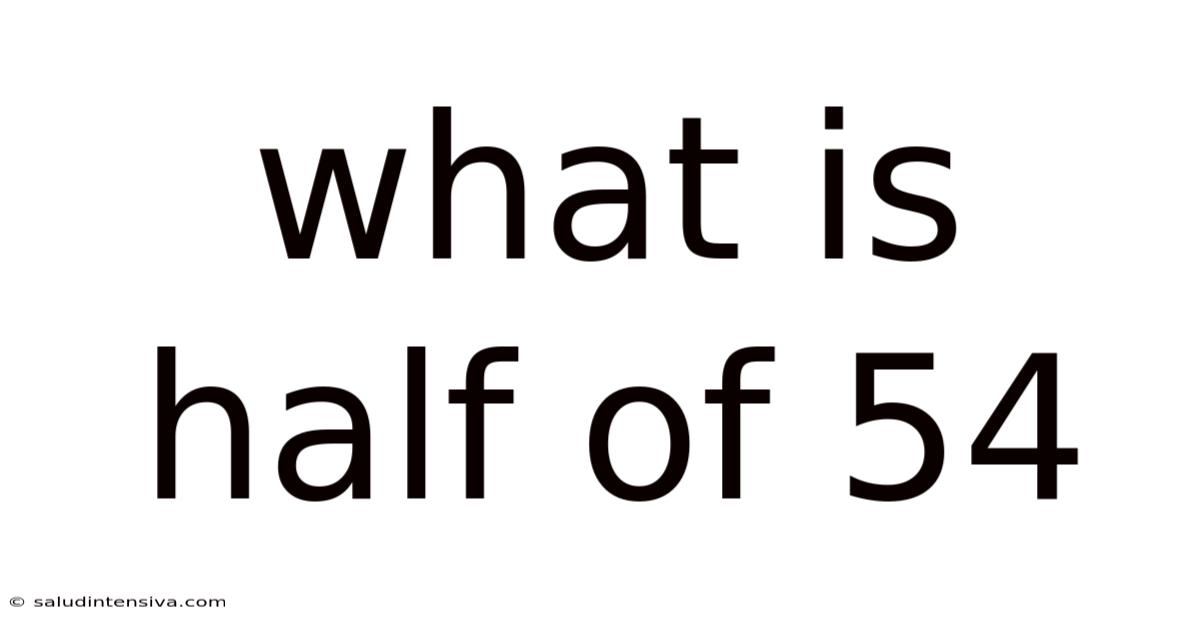
Table of Contents
What is Half of 54? A Deep Dive into Division and Beyond
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life and advanced calculations. This seemingly simple question, "What is half of 54?", opens the door to exploring various mathematical concepts, from basic arithmetic to more abstract ideas. This article will not only answer the question directly but also delve into the underlying principles, practical applications, and related mathematical concepts. We'll explore different methods of solving this problem, addressing potential misconceptions and providing a comprehensive understanding of the topic.
Understanding Division and Fractions
The phrase "half of 54" essentially means dividing 54 by 2. Division is the inverse operation of multiplication. If we multiply a number by 2, we are essentially doubling it. Division by 2, therefore, is the process of finding half of that number. This relates directly to the concept of fractions. "Half" is represented by the fraction ½. Therefore, finding half of 54 is equivalent to calculating ½ x 54 or 54 ÷ 2.
Methods for Finding Half of 54
Several methods can be used to find half of 54:
1. Direct Division: This is the most straightforward approach. We simply divide 54 by 2:
54 ÷ 2 = 27
Therefore, half of 54 is 27.
2. Repeated Subtraction: While less efficient for larger numbers, repeated subtraction provides a visual understanding of division. We can subtract 2 repeatedly from 54 until we reach 0. The number of times we subtract 2 represents half of 54.
54 - 2 = 52 52 - 2 = 50 50 - 2 = 48 ...and so on until we reach 0. Counting the number of subtractions will yield 27.
3. Fraction Multiplication: As mentioned earlier, finding half of a number is the same as multiplying the number by ½.
½ x 54 = 27
This method showcases the connection between fractions and division. We can also express ½ as a decimal (0.5), and the calculation becomes:
0.5 x 54 = 27
4. Mental Math Techniques: With practice, you can develop mental math strategies for quickly finding half of numbers. For example, you can break down 54 into easier numbers:
- Think of 54 as 50 + 4.
- Half of 50 is 25.
- Half of 4 is 2.
- Add the halves together: 25 + 2 = 27
Expanding the Concept: Halving Larger Numbers
The principle of finding half remains consistent regardless of the number's size. Let's consider finding half of larger numbers to illustrate the concept further.
- Half of 100: 100 ÷ 2 = 50
- Half of 250: 250 ÷ 2 = 125
- Half of 1000: 1000 ÷ 2 = 500
Observe the pattern: dividing by 2 always results in a number exactly half the original value. This fundamental principle is used extensively in various applications.
Real-World Applications of Halving
The concept of halving has numerous practical applications in everyday life:
- Sharing Equally: Dividing resources equally among two people involves halving. For example, splitting a bill in a restaurant or sharing a snack with a friend.
- Cooking and Baking: Many recipes require halving or doubling ingredients to adjust the serving size.
- Measurement and Construction: Halving measurements is crucial in various construction and engineering projects.
- Data Analysis and Statistics: Finding the median (middle value) of a dataset often involves halving the number of data points.
- Geometry: Halving lines or shapes is fundamental to understanding geometric concepts.
- Financial Calculations: Interest calculations, profit-sharing, and budgeting often involve halving or proportional divisions.
Misconceptions and Common Errors
A common misconception is confusing halving with subtracting 2. These are distinct operations. Subtracting 2 from 54 results in 52, not 27. Always remember that halving involves dividing by 2.
Advanced Concepts: Beyond Halving
The concept of halving extends to understanding other fractions and percentages. For example:
- Finding a quarter (¼) of 54: This involves dividing 54 by 4 (or multiplying by ¼), resulting in 13.5.
- Finding 25% of 54: This is equivalent to finding a quarter of 54, also resulting in 13.5.
- Finding a third (⅓) of 54: This involves dividing 54 by 3, resulting in 18.
Understanding these relationships is crucial for building a strong foundation in mathematics.
The Importance of Mathematical Foundations
The ability to quickly and accurately find half of a number demonstrates a grasp of fundamental mathematical principles. This skill is not just limited to solving simple problems; it's a building block for more complex mathematical concepts and applications in various fields.
Further Exploration: Related Mathematical Concepts
Exploring the concept of "half of 54" opens doors to numerous related concepts:
- Even and Odd Numbers: The fact that 54 is an even number ensures that its half is a whole number. Odd numbers, when halved, result in a fraction or decimal.
- Prime Factorization: Understanding prime factors (2, 3) of 54 can offer insight into its divisibility.
- Decimal Representation: Expressing fractions as decimals helps in performing calculations.
- Proportions and Ratios: Halving is a simple form of proportion; it represents a ratio of 1:2.
- Algebra: The concept of halving can be expressed algebraically: x/2, where x represents the number.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between halving and dividing by 2?
A: Halving and dividing by 2 are essentially the same operation. They both result in finding half of a number.
-
Q: How do I find half of a decimal number?
A: You divide the decimal number by 2 using the same methods as for whole numbers.
-
Q: Can I halve a negative number?
A: Yes, halving a negative number results in a negative number. For example, half of -54 is -27.
-
Q: What if I need to find more than half of a number?
A: To find a larger fraction (e.g., ⅔ of 54), you would multiply the number by the fraction (⅔ x 54 = 36).
-
Q: How can I improve my mental math skills for halving?
A: Practice is key! Start with easy numbers, gradually increasing the complexity. Try breaking down numbers into smaller, easier-to-halve parts.
Conclusion:
While the answer to "What is half of 54?" is simply 27, this seemingly straightforward question unveils a wealth of mathematical concepts. Understanding division, fractions, and the various methods for halving numbers lays a strong foundation for more advanced mathematical explorations. The ability to quickly and accurately halve numbers is a valuable skill applicable across numerous fields, demonstrating the importance of mastering fundamental mathematical principles. This article has provided a comprehensive exploration, ensuring a deeper understanding of this essential concept. Remember that mathematical fluency is built upon a solid understanding of fundamental concepts like halving, and continued practice will refine your abilities.
Latest Posts
Latest Posts
-
20 4 In Decimal Form
Sep 18, 2025
-
19 4 As A Decimal
Sep 18, 2025
-
4 To The 3rd Power
Sep 18, 2025
-
Convert 175 C To Fahrenheit
Sep 18, 2025
-
What Is Equivalent To 6 12
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.