What Is Half Of 67
saludintensiva
Sep 17, 2025 · 5 min read
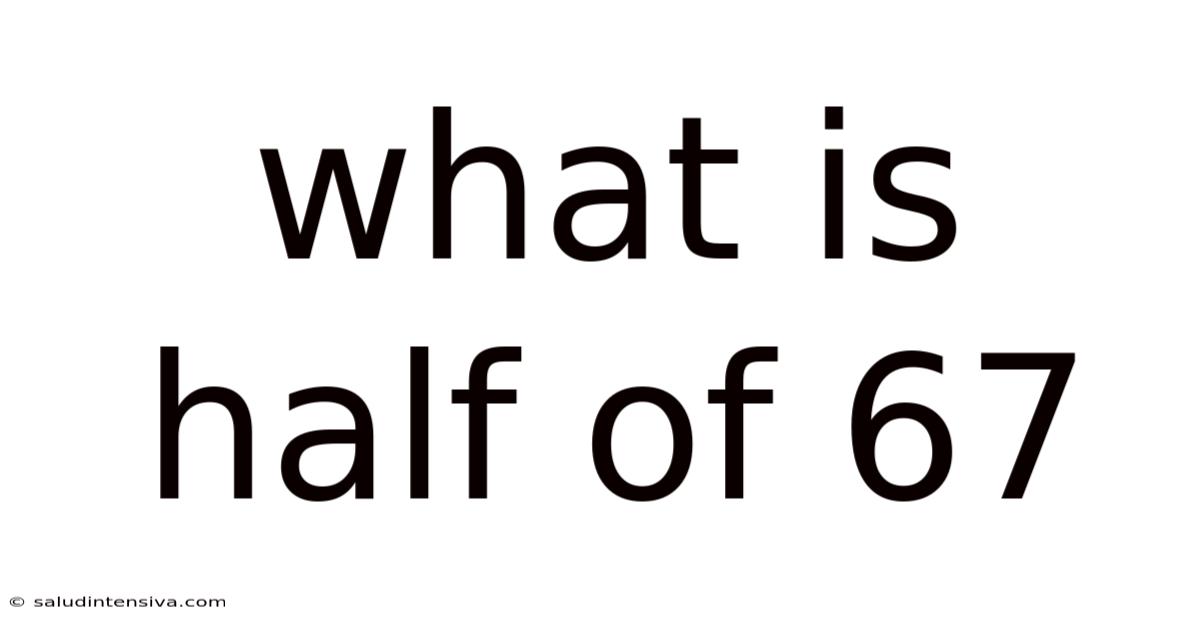
Table of Contents
What is Half of 67? A Deep Dive into Division and Fractions
What is half of 67? This seemingly simple question opens a door to a fascinating exploration of mathematical concepts, from basic arithmetic to the nuances of fractions and decimals. While the immediate answer is straightforward, understanding the why behind the calculation unlocks a deeper appreciation for mathematical principles and their real-world applications. This article will not only answer the question directly but also delve into the methods for solving it, explain the underlying mathematical concepts, and explore related applications.
Understanding the Concept of "Half"
Before tackling the problem, let's clarify the meaning of "half." Half represents one of two equal parts of a whole. This concept is fundamental to understanding fractions and division. When we say "half of 67," we're essentially asking for the result of dividing 67 into two equal parts.
Methods for Finding Half of 67
There are several ways to calculate half of 67:
1. Division: The most direct method is simple division. We divide 67 by 2:
67 ÷ 2 = 33.5
Therefore, half of 67 is 33.5.
2. Fraction Representation: "Half" can be represented as the fraction 1/2. To find half of 67, we multiply 67 by 1/2:
67 × (1/2) = 67/2 = 33.5
This method reinforces the connection between fractions and division.
3. Decimal Conversion: We can also think of "half" as 0.5. Multiplying 67 by 0.5 yields the same result:
67 × 0.5 = 33.5
This highlights the interchangeability between fractions and decimals.
Why the Answer is 33.5: A Deeper Look
The answer, 33.5, is a decimal number. This arises because 67 is an odd number. When we divide an odd number by 2, the result will always be a decimal, representing a whole number and a half. If we were dealing with an even number, the result would be a whole number. For example, half of 68 is 34.
This distinction highlights the importance of understanding number properties – odd and even numbers – in arithmetic. The concept of even and odd numbers is crucial in many areas of mathematics, including number theory and algebra.
Exploring Fractions and Decimals: A Necessary Excursion
The calculation above inherently involves fractions and decimals. Let's delve a bit deeper into these concepts:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In the case of "half," the fraction is 1/2, where 1 is the numerator and 2 is the denominator. The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we are considering.
-
Decimals: Decimals are another way to represent fractions. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. 33.5 is a decimal representing 33 and 5/10, which simplifies to 33 and 1/2.
Real-World Applications: Where This Matters
The seemingly simple task of finding half of 67 has far-reaching applications in various real-world scenarios:
-
Sharing Equally: Imagine you have 67 cookies to share equally between two friends. Each friend would receive 33.5 cookies. While you can't physically split a cookie exactly in half, the calculation helps you understand the fair distribution.
-
Measurement and Conversion: In construction or cooking, you might need to halve a measurement. If a recipe calls for 67 grams of flour, halving it requires the same calculation.
-
Financial Calculations: Dividing amounts of money is common. If you want to split a $67 bill equally between two people, each person owes $33.50.
-
Data Analysis and Statistics: Calculating averages often involves division. If you have two measurements, 67 and x, and their average is y, you might need to solve for x using equations involving halving.
-
Geometry and Area Calculations: The concept of halving is used extensively in geometrical calculations. Finding the area of a triangle, for instance, involves halving the base times height.
Beyond the Basics: Extending the Concept
The question "What is half of 67?" can be extended to more complex scenarios:
-
Finding a Fraction Other Than Half: Instead of half (1/2), you might need to find a third (1/3), a quarter (1/4), or any other fraction of 67. This requires understanding fraction multiplication and division.
-
Working with Larger Numbers: The same principles apply to finding half of much larger numbers. The process remains the same, although the calculations might be more involved.
-
Solving Word Problems: Real-world applications often involve word problems that require interpreting the situation and applying the appropriate mathematical operation, such as finding half of a quantity.
Frequently Asked Questions (FAQ)
Q: What if I need to find more than half of 67?
A: If you need to find, for example, three-quarters (3/4) of 67, you would multiply 67 by 3/4: 67 × (3/4) = 50.25
Q: How can I calculate half of 67 without a calculator?
A: You can perform long division: Divide 67 by 2. The quotient will be 33, and the remainder will be 1. The remainder represents 1/2, or 0.5. Therefore, the answer is 33.5.
Q: What is the difference between dividing by 2 and multiplying by 0.5?
A: They are mathematically equivalent. Multiplying by 0.5 is the same as multiplying by 1/2, which is the same as dividing by 2. They all represent the same operation of finding half of a number.
Q: Why is it important to understand the concept of "half"?
A: Understanding the concept of "half" is fundamental to arithmetic, fractions, and many other areas of mathematics. It's also crucial for everyday life, from sharing resources fairly to performing simple calculations in various contexts.
Conclusion
The seemingly simple question of "What is half of 67?" opens a rich vein of mathematical exploration. The answer, 33.5, is more than just a number; it represents a deeper understanding of fractions, decimals, division, and their practical applications in numerous real-world scenarios. By exploring this seemingly simple calculation, we've touched upon fundamental concepts that are essential for mathematical literacy and problem-solving skills. The key takeaway is that understanding the why behind a calculation is just as important, if not more so, than obtaining the numerical answer itself. This deeper understanding enables us to apply these principles confidently and effectively in various situations.
Latest Posts
Latest Posts
-
What Are Multiples Of 100
Sep 17, 2025
-
37 20 As A Decimal
Sep 17, 2025
-
200 Percent In Decimal Form
Sep 17, 2025
-
17 3 As A Mixed Number
Sep 17, 2025
-
1 2 5 As A Percent
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 67 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.