What Percent Is 5 8
saludintensiva
Sep 15, 2025 · 5 min read
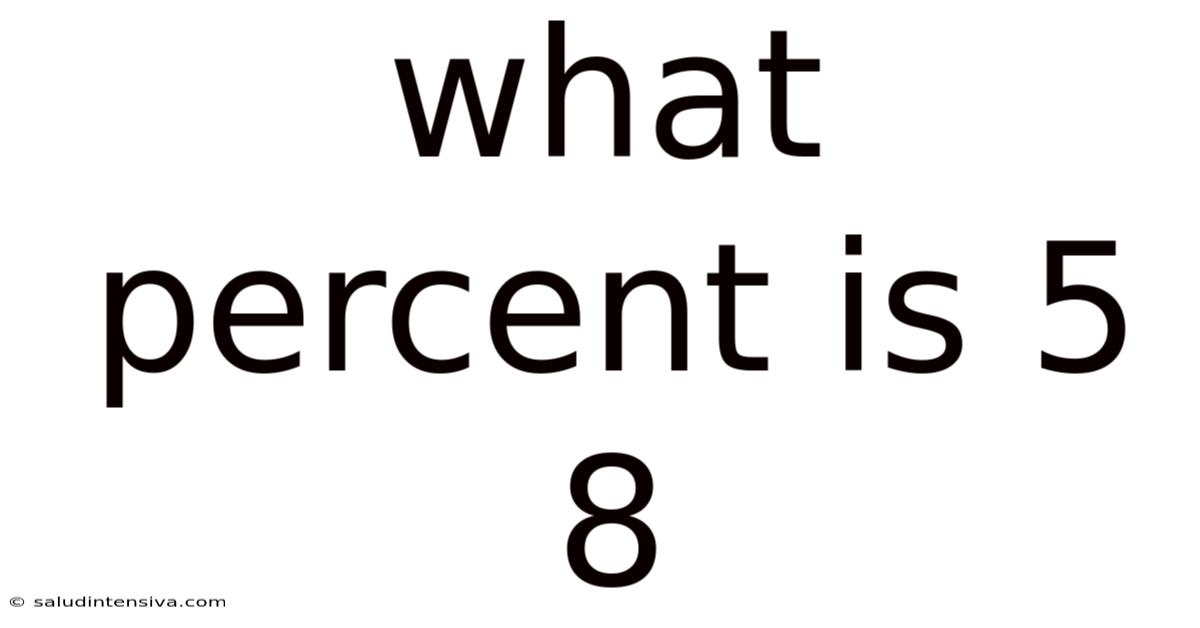
Table of Contents
What Percent is 5/8? A Deep Dive into Fractions, Decimals, and Percentages
Understanding fractions, decimals, and percentages is fundamental to everyday life, from calculating discounts in a shop to comprehending statistical data. This article will explore how to determine what percentage 5/8 represents, providing a thorough explanation suitable for learners of all levels. We'll delve into the underlying mathematical principles, explore different calculation methods, and address common questions about converting fractions to percentages. This comprehensive guide aims to solidify your understanding of this essential mathematical concept.
Understanding Fractions, Decimals, and Percentages
Before calculating the percentage equivalent of 5/8, let's refresh our understanding of these three interconnected concepts:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/8, 5 is the numerator and 8 is the denominator. This signifies 5 parts out of a total of 8 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with a decimal point separating the whole number from the fractional part. For instance, 0.5 represents one-half (1/2), and 0.75 represents three-quarters (3/4).
-
Percentages: Percentages express a fraction or decimal as a proportion of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is arguably the most straightforward method to determine what percent 5/8 is. It involves two steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator:
5 ÷ 8 = 0.625
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.625 x 100 = 62.5%
Therefore, 5/8 is equal to 62.5%.
Method 2: Using Equivalent Fractions
This method leverages the principle that equivalent fractions represent the same value. The goal is to find an equivalent fraction where the denominator is 100. While this method isn't always practical for all fractions, it's useful for understanding the underlying relationships.
To find an equivalent fraction with a denominator of 100, we need to find a number that, when multiplied by 8, equals 100. Unfortunately, there isn't a whole number that satisfies this condition. However, we can use a slightly different approach: We can aim for a denominator that's easily convertible to a percentage. Let's consider how to convert the fraction to have a denominator that is a factor of 100. This is more easily understood with simpler examples first.
Let's consider 1/4 as an example. To convert 1/4 to a percentage, we would multiply both the numerator and denominator by 25 to achieve a denominator of 100:
(1 x 25) / (4 x 25) = 25/100 = 25%
Now back to 5/8. We can't easily find a whole number to multiply the denominator (8) to get 100. However, we can still use the first method (converting to a decimal and then to a percentage) which is much more efficient.
Method 3: Proportions
This method uses the concept of proportions to solve for the unknown percentage. We can set up a proportion:
5/8 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
8x = 500
Now, we divide both sides by 8:
x = 500 ÷ 8 = 62.5
Therefore, x = 62.5%, confirming our previous results. This method showcases the versatility of proportions in solving percentage problems.
The Importance of Understanding Percentage Calculations
Mastering percentage calculations is crucial for numerous reasons:
-
Financial Literacy: Calculating interest rates, discounts, taxes, tips, and investment returns all rely on understanding percentages.
-
Data Analysis: Percentages are widely used to represent data in graphs, charts, and reports, making it essential to interpret and analyze them accurately.
-
Everyday Applications: From understanding sale prices to calculating recipe proportions, percentages are integral to our daily lives.
-
Academic Success: Proficiency in percentage calculations is vital for success in various academic subjects, including mathematics, science, and economics.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to find the percentage?
A1: Absolutely! Most calculators have a percentage function that simplifies the process. You can either divide the numerator by the denominator and then multiply by 100, or you can directly input the fraction and use the calculator's percentage function.
Q2: What if the fraction has a larger numerator than denominator (improper fraction)?
A2: An improper fraction (where the numerator is larger than the denominator) represents a value greater than 1. You still follow the same conversion process: divide the numerator by the denominator to get a decimal, then multiply by 100 to get the percentage. The resulting percentage will be greater than 100%.
Q3: Are there any other ways to express 5/8?
A3: Yes! Besides 62.5%, 5/8 can also be expressed as a decimal (0.625) or as an equivalent fraction (e.g., 25/40, 100/160). The choice of representation depends on the context and desired level of precision.
Q4: How can I improve my understanding of fractions, decimals, and percentages?
A4: Consistent practice is key. Try solving various problems involving conversions between these three forms. You can find numerous practice exercises online or in textbooks. Focus on understanding the underlying concepts, rather than just memorizing formulas. Breaking down complex problems into smaller, manageable steps will also aid your understanding.
Conclusion
Determining that 5/8 is equal to 62.5% is a straightforward calculation, but the underlying principles of fractions, decimals, and percentages are much broader and more significant. Understanding these concepts empowers you to confidently tackle various mathematical problems in diverse settings. By mastering these foundational skills, you'll enhance your ability to interpret data, manage finances, and approach problem-solving with increased confidence and competence. Remember, consistent practice and a firm grasp of the core concepts are crucial to mastering these essential mathematical skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.