What Percentage Is 2 5
saludintensiva
Sep 16, 2025 · 6 min read
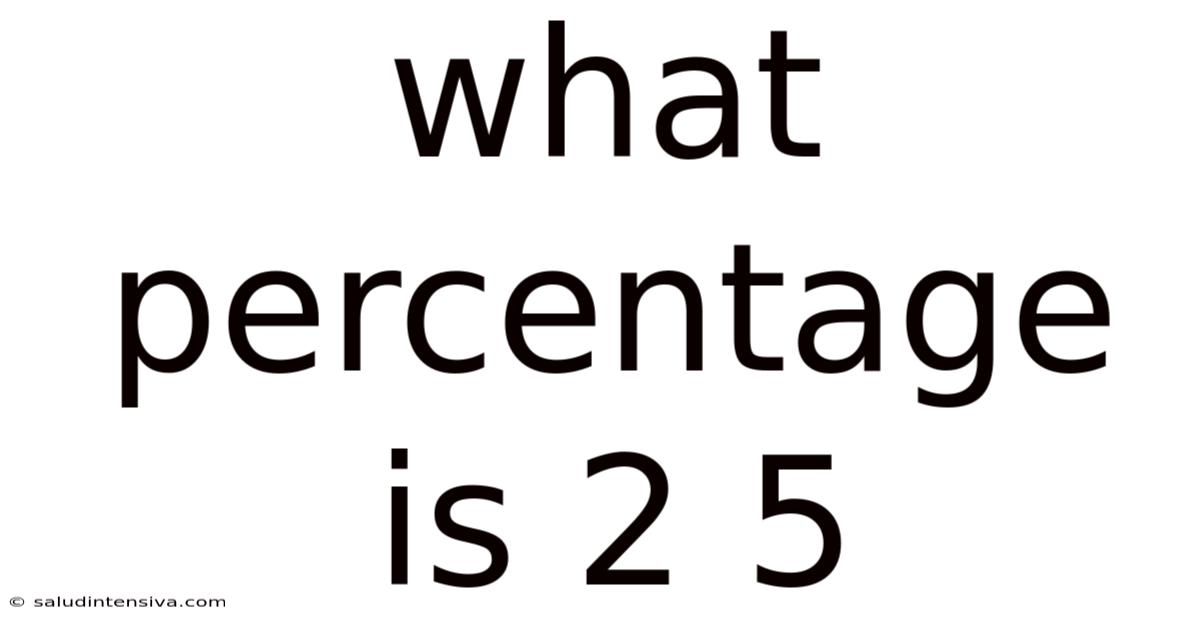
Table of Contents
What Percentage is 2 of 5? A Deep Dive into Fractions, Decimals, and Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will explore the seemingly simple question, "What percentage is 2 of 5?", but in doing so, we'll delve much deeper than a simple answer. We'll cover the underlying concepts of fractions, decimals, and percentages, providing a comprehensive understanding of how these mathematical tools relate to each other and how to solve similar problems effectively. This guide will be particularly helpful for students learning about percentages and anyone looking to solidify their understanding of these essential mathematical concepts.
Understanding Fractions
Before we tackle percentages, it's crucial to understand fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In our example, "2 of 5" can be represented as the fraction 2/5. The numerator, 2, represents the part, and the denominator, 5, represents the whole.
Think of it this way: if you have 5 apples and you take 2, the fraction 2/5 represents the portion of apples you've taken compared to the total number of apples.
Converting Fractions to Decimals
To convert a fraction to a decimal, you simply divide the numerator by the denominator. In our case:
2 ÷ 5 = 0.4
So, the fraction 2/5 is equivalent to the decimal 0.4.
Converting Decimals to Percentages
A percentage is simply a fraction or decimal expressed as a part of 100. To convert a decimal to a percentage, you multiply the decimal by 100 and add the "%" symbol. This is because "percent" literally means "per hundred".
0.4 x 100 = 40
Therefore, 0.4 is equivalent to 40%.
Putting it All Together: What Percentage is 2 of 5?
Combining the steps above, we can definitively answer the question: 2 is 40% of 5.
This simple calculation illustrates the interconnectedness of fractions, decimals, and percentages. They are different ways of representing the same proportional relationship. Mastering the conversions between these forms is vital for understanding and solving a wide array of mathematical problems.
The Formula for Calculating Percentages
The process we've just gone through can be generalized into a formula:
(Part / Whole) x 100% = Percentage
In our example:
(2 / 5) x 100% = 40%
This formula can be used to calculate the percentage of any part relative to its whole. Simply substitute the values of the "part" and the "whole" into the formula to find the percentage.
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly useful in a variety of real-world situations. Here are just a few examples:
-
Calculating Discounts: If a store offers a 20% discount on a $50 item, you can easily calculate the discount amount: (20/100) x $50 = $10. The final price would be $50 - $10 = $40.
-
Determining Tax Amounts: Similarly, you can use percentages to calculate sales tax. If the tax rate is 6% and the item costs $100, the tax amount is (6/100) x $100 = $6.
-
Understanding Financial Statements: Percentages are frequently used in financial statements to show ratios, such as profit margins, debt-to-equity ratios, and return on investment (ROI).
-
Interpreting Statistics: Percentages are essential for understanding and interpreting statistical data, such as survey results, election polls, and market research findings.
-
Calculating Grades and Scores: In education, percentages are commonly used to represent grades and scores on tests and assignments.
-
Working with Proportions: Percentages are fundamentally about proportions, making them vital in fields such as recipe scaling, map scaling, and model building.
More Complex Percentage Problems
While the example of 2/5 is relatively straightforward, let's explore some more complex scenarios to further solidify your understanding:
Scenario 1: Finding the Whole
Let's say 30% of a number is 12. How do we find the original number (the whole)?
We can set up the equation:
(30/100) x Whole = 12
To solve for "Whole," we can rearrange the equation:
Whole = 12 / (30/100) = 12 x (100/30) = 40
Therefore, the whole number is 40.
Scenario 2: Finding the Part
If 15% of a class of 20 students are absent, how many students are absent?
(15/100) x 20 = 3
3 students are absent.
Scenario 3: Percentage Increase/Decrease
A product's price increased from $25 to $30. What is the percentage increase?
First, calculate the difference: $30 - $25 = $5
Then, divide the difference by the original price and multiply by 100%:
($5 / $25) x 100% = 20%
The price increased by 20%.
Common Mistakes to Avoid When Working with Percentages
-
Confusing Part and Whole: Carefully identify the "part" and the "whole" in the problem to avoid incorrect calculations.
-
Incorrectly Converting Fractions and Decimals: Ensure accurate conversions between fractions, decimals, and percentages to maintain accuracy.
-
Misinterpreting Percentage Increase/Decrease: Remember to calculate the percentage increase or decrease relative to the original value.
Frequently Asked Questions (FAQ)
Q: What is the simplest way to calculate percentages?
A: The simplest way is to use the formula: (Part / Whole) x 100% = Percentage. You can also use a calculator or online percentage calculator for convenience.
Q: How do I calculate a percentage of a number quickly in my head?
A: For easy percentages like 10%, 20%, 50%, simply move the decimal point. For other percentages, you might need to break them down into easier parts (e.g., 15% is 10% + 5%).
Q: What resources can help me practice calculating percentages?
A: Numerous online resources, including educational websites and apps, offer practice problems and tutorials on percentage calculations. Textbooks and workbooks are also excellent resources.
Q: Are there any shortcuts for calculating percentages?
A: Yes, there are various shortcuts depending on the specific problem. For example, calculating 10% involves simply moving the decimal point one place to the left. Understanding these shortcuts can significantly speed up calculations.
Conclusion
Understanding percentages is a critical skill applicable across various fields. While the question of "What percentage is 2 of 5?" might seem simple, exploring its answer reveals the underlying principles of fractions, decimals, and percentages, and how they interconnect. Mastering these concepts allows you to confidently tackle more complex percentage problems and confidently apply your knowledge to real-world situations. Remember to practice regularly and use the formula (Part / Whole) x 100% = Percentage as your guide. With consistent practice, you'll build a strong foundation in this essential area of mathematics. Remember that math is a journey, not a destination, and continuous learning will always lead to greater understanding and problem-solving abilities.
Latest Posts
Latest Posts
-
Half Of 1 2 Inch
Sep 16, 2025
-
Changing Decimals To Mixed Numbers
Sep 16, 2025
-
Adding Fractions Negative And Positive
Sep 16, 2025
-
43560 Square Feet To Feet
Sep 16, 2025
-
14 To The Second Power
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.