What Times What Equals 42
saludintensiva
Sep 20, 2025 · 6 min read
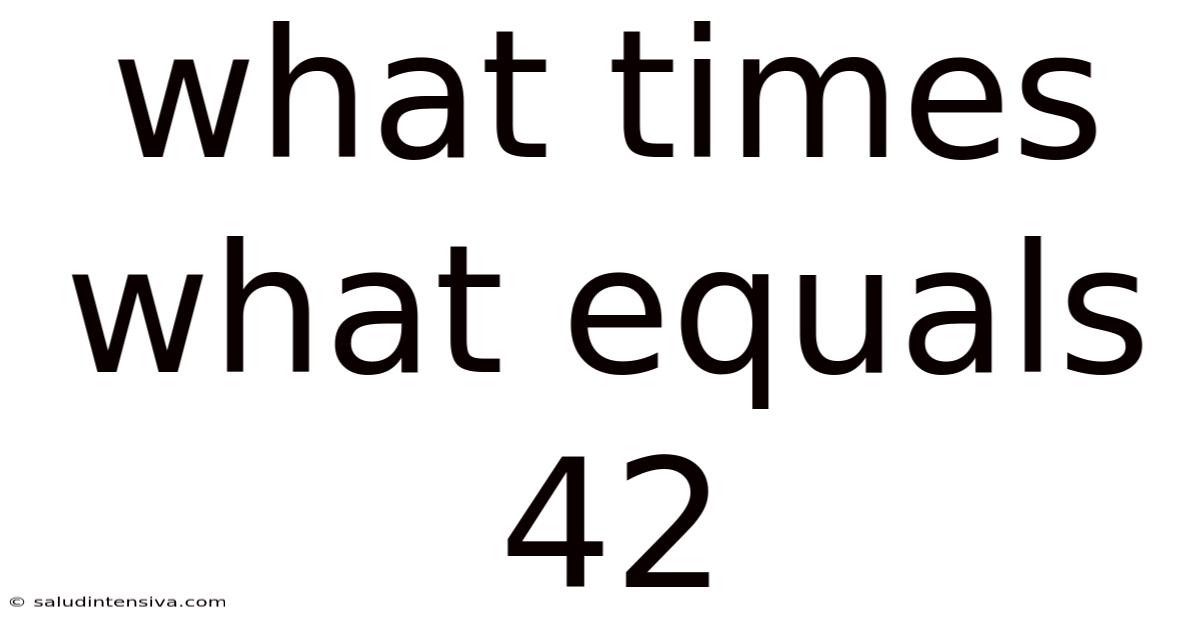
Table of Contents
What Times What Equals 42? Exploring the Factors and Applications of 42
The seemingly simple question, "What times what equals 42?" opens a door to a surprisingly rich world of mathematical concepts, problem-solving strategies, and even a touch of cultural intrigue. This seemingly basic arithmetic problem touches upon fundamental concepts in number theory and can be approached in various ways, depending on the level of mathematical sophistication desired. This article will explore different methods for finding the factors of 42, discuss the importance of factor pairs, delve into the broader context of factorization, and finally, touch upon the cultural significance of the number 42.
Understanding Factors and Factor Pairs
Before diving into the solutions to "what times what equals 42," let's clarify the core mathematical concepts involved. A factor of a number is a whole number that divides that number evenly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
A factor pair is a set of two factors whose product equals the given number. For the number 12, some factor pairs are (1, 12), (2, 6), and (3, 4). Finding all factor pairs is crucial for completely understanding the multiplicative structure of a number.
Finding the Factor Pairs of 42
Now, let's tackle the original question: "What times what equals 42?" This is essentially asking us to find all the factor pairs of 42. We can approach this systematically:
- Start with 1: Since 1 is a factor of every number, we know that (1, 42) is a factor pair.
- Consider 2: 42 is an even number, so it's divisible by 2. 42 divided by 2 is 21, giving us the factor pair (2, 21).
- Consider 3: The sum of the digits of 42 (4 + 2 = 6) is divisible by 3, indicating that 42 itself is divisible by 3. 42 divided by 3 is 14, yielding the factor pair (3, 14).
- Consider 6: Since 2 and 3 are factors, their product (6) must also be a factor. 42 divided by 6 is 7, leading to the factor pair (6, 7).
- Consider 7: We've already found that 7 is a factor (from the (6,7) pair).
- Consider higher numbers: We've now considered all factors up to the square root of 42 (approximately 6.48). Any factors larger than 6 would already have been identified as the second part of a pair we’ve already found.
Therefore, the factor pairs of 42 are: (1, 42), (2, 21), (3, 14), (6, 7). These are all the possible combinations of two whole numbers that multiply to equal 42.
Beyond Basic Factorization: Prime Factorization
The process of finding factor pairs can be further refined using the concept of prime factorization. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization involves expressing a number as the product of its prime factors.
To find the prime factorization of 42, we can use a factor tree:
42 = 2 x 21 21 = 3 x 7
Therefore, the prime factorization of 42 is 2 x 3 x 7. This representation is unique to 42 and is a fundamental concept in number theory. Understanding prime factorization helps us understand the fundamental building blocks of a number and aids in solving more complex mathematical problems.
Applications of Factorization: Real-World Examples
The ability to find factors and factor pairs has numerous applications beyond basic arithmetic:
- Algebra: Factoring is a crucial technique in solving algebraic equations. For instance, when solving quadratic equations, we often need to factor expressions to find the roots.
- Geometry: Understanding factors is essential in various geometric problems, such as finding the dimensions of rectangles with a given area. If the area is 42 square units, possible dimensions could be 1 unit by 42 units, 2 units by 21 units, 3 units by 14 units, or 6 units by 7 units.
- Cryptography: Prime factorization plays a vital role in modern cryptography, particularly in algorithms like RSA encryption. The difficulty of factoring very large numbers into their prime factors forms the basis of the security of these systems.
- Computer Science: Factorization is used in various algorithms and data structures. Efficient factorization techniques are crucial for optimizing performance in certain computational tasks.
Addressing Potential Misconceptions
It's important to address some common misconceptions related to finding factors:
- Negative Factors: While we've focused on positive factors, it's important to remember that negative numbers can also be factors. For example, (-1, -42), (-2, -21), (-3, -14), and (-6, -7) are also factor pairs of 42 because (-1) x (-42) = 42, and so on.
- Fractional Factors: We've restricted ourselves to whole number factors. However, if we allowed fractions, an infinite number of pairs would exist. For example, (1/2, 84), (1/3, 126), etc., all multiply to 42. But these are beyond the scope of the original question.
Frequently Asked Questions (FAQ)
Q: Is 42 a prime number?
A: No, 42 is not a prime number. A prime number has only two factors: 1 and itself. 42 has multiple factors (1, 2, 3, 6, 7, 14, 21, 42).
Q: What are the factors of 42?
A: The factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42.
Q: How many factor pairs does 42 have?
A: 42 has four factor pairs: (1, 42), (2, 21), (3, 14), and (6, 7). If we consider negative factors, there are eight pairs.
Q: What is the prime factorization of 42?
A: The prime factorization of 42 is 2 x 3 x 7.
The Cultural Significance of 42
Beyond its mathematical properties, the number 42 holds a peculiar cultural significance, primarily due to its appearance in Douglas Adams's The Hitchhiker's Guide to the Galaxy. In the book, 42 is revealed as the "Answer to the Ultimate Question of Life, the Universe, and Everything," calculated by a supercomputer named Deep Thought. The humor lies in the fact that the question itself is never revealed, leaving the number 42 shrouded in mystery and sparking much speculation and fan theories. This cultural association has cemented 42's place in popular culture, often appearing as an Easter egg or reference in various media.
Conclusion
The seemingly simple question, "What times what equals 42?" leads to a fascinating exploration of fundamental mathematical concepts. By finding its factor pairs and prime factorization, we delve into the rich structure of numbers and uncover their applications in various fields. Moreover, the cultural intrigue surrounding 42 adds another layer to its multifaceted nature, making it a number with both mathematical depth and popular appeal. So, the next time you encounter this seemingly simple question, remember the wealth of mathematical knowledge and cultural intrigue hidden within the answer.
Latest Posts
Latest Posts
-
21 Cm How Many Inches
Sep 20, 2025
-
9600 Sq Ft To Acres
Sep 20, 2025
-
Is Ten A Perfect Square
Sep 20, 2025
-
Ft Cubed To Inches Cubed
Sep 20, 2025
-
Cubic Foot Of Soil Weight
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.