What's 1.3 As A Fraction
saludintensiva
Sep 16, 2025 · 5 min read
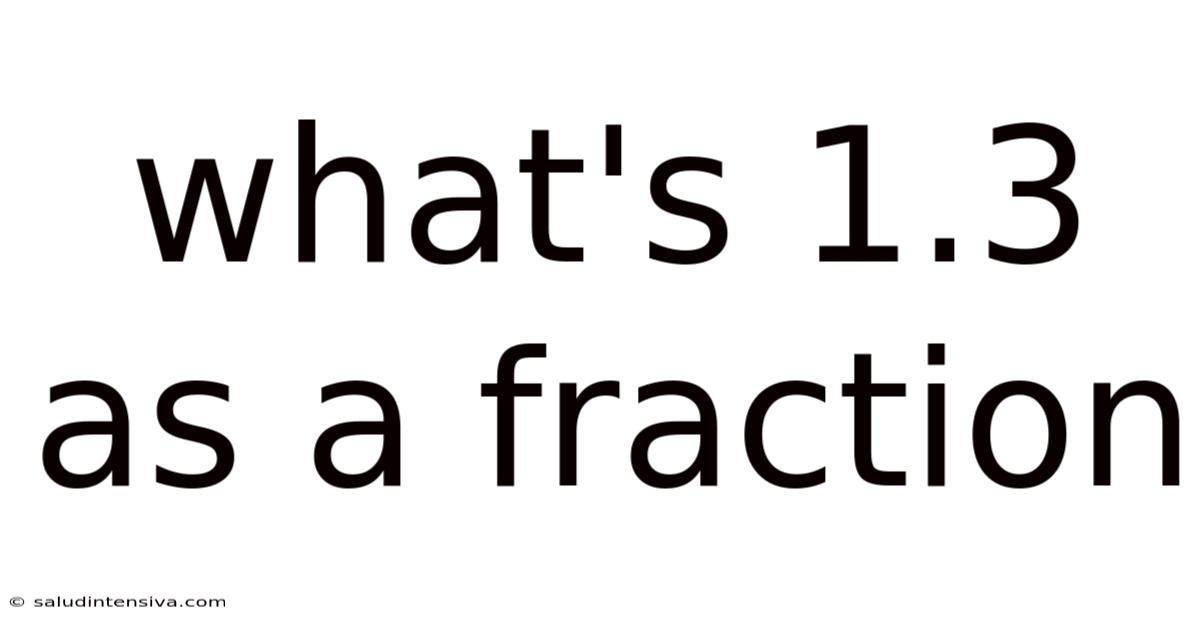
Table of Contents
Decoding 1.3: A Deep Dive into Decimal to Fraction Conversion
Understanding how to convert decimals to fractions is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide will explore the conversion of the decimal 1.3 into its fractional equivalent, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions. By the end, you'll not only know that 1.3 is equal to 13/10 but also understand why this is the case, and be equipped to handle similar conversions with confidence.
Understanding Decimals and Fractions
Before we embark on the conversion of 1.3, let's briefly review the concepts of decimals and fractions. Decimals represent numbers as a sum of powers of ten. The number 1.3, for example, can be broken down as 1 + 0.3, where 0.3 represents three-tenths (3/10).
Fractions, on the other hand, represent a part of a whole, expressed as a ratio of two integers: the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Converting 1.3 to a Fraction: A Step-by-Step Guide
Converting 1.3 to a fraction involves several straightforward steps:
Step 1: Identify the Decimal Part
The decimal 1.3 consists of a whole number part (1) and a decimal part (0.3). We'll focus on converting the decimal part first.
Step 2: Express the Decimal Part as a Fraction
The decimal part, 0.3, means "three-tenths". This can be directly expressed as a fraction: 3/10.
Step 3: Combine the Whole Number and Fractional Parts
Now, we combine the whole number part (1) with the fractional part (3/10). This can be represented as:
1 + 3/10
Step 4: Convert the Whole Number to an Improper Fraction (Optional but Helpful)
To express the entire number as a single fraction, we need to convert the whole number 1 into a fraction with a denominator of 10 (to match the fractional part). This gives us 10/10.
Step 5: Add the Fractions
Now we add the two fractions:
10/10 + 3/10 = 13/10
Therefore, 1.3 as a fraction is 13/10. This is an improper fraction because the numerator (13) is larger than the denominator (10).
Alternative Method: Using Place Value
Another approach involves directly considering the place value of the digits in the decimal. In 1.3, the digit 3 is in the tenths place. Therefore, it represents 3/10. Combining this with the whole number 1, we again arrive at 13/10.
Converting Improper Fractions to Mixed Numbers
While 13/10 is perfectly valid, it's often preferable to express improper fractions as mixed numbers. A mixed number consists of a whole number and a proper fraction (numerator smaller than the denominator).
To convert 13/10 to a mixed number, we perform a division:
13 ÷ 10 = 1 with a remainder of 3.
This means 13/10 is equal to 1 and 3/10, or 1 3/10. Both 13/10 and 1 3/10 represent the same value, just in different forms.
Simplifying Fractions
In some cases, fractions can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. However, in the case of 13/10, the GCD of 13 and 10 is 1. Since dividing by 1 doesn't change the value, the fraction 13/10 is already in its simplest form.
The Importance of Understanding Decimal to Fraction Conversions
The ability to convert decimals to fractions and vice versa is not just a mathematical exercise; it's a crucial skill with numerous real-world applications:
- Baking and Cooking: Recipes often require fractional measurements, while some digital scales provide decimal readings.
- Engineering and Construction: Precise measurements are essential, and converting between decimals and fractions allows for accurate calculations and conversions between different measurement systems.
- Finance: Calculations involving percentages, interest rates, and stock prices often involve working with both decimals and fractions.
- Data Analysis: In statistical analysis, converting between decimals and fractions can facilitate calculations and interpretations.
Frequently Asked Questions (FAQ)
Q1: Can all decimals be converted to fractions?
A1: Yes, all terminating decimals (decimals that end after a finite number of digits) and repeating decimals (decimals with a repeating pattern of digits) can be expressed as fractions. Non-repeating, non-terminating decimals (like π) cannot be expressed as a simple fraction.
Q2: What if the decimal has more than one digit after the decimal point?
A2: The process remains similar. For example, to convert 2.56 to a fraction:
- 0.56 represents 56 hundredths, or 56/100.
- Combining with the whole number 2, we get 2 + 56/100 = 256/100. This can be simplified to 64/25 or 2 14/25.
Q3: Why is it important to learn different methods for decimal to fraction conversion?
A3: Different methods offer flexibility and cater to different learning styles and problem-solving approaches. Understanding multiple methods allows you to choose the most efficient and intuitive method for each specific problem.
Q4: Are there any online tools or calculators to help with decimal to fraction conversions?
A4: While many online calculators can perform this conversion, the most important aspect is understanding the underlying mathematical principles. These calculators can be helpful for checking answers but shouldn't replace a solid grasp of the conversion process.
Conclusion
Converting decimals to fractions is a fundamental mathematical skill with wide-ranging applications. This detailed explanation of the conversion of 1.3 to 13/10 (or 1 3/10) demonstrates a straightforward process that can be applied to other decimal-to-fraction conversions. Remember, understanding the underlying principles—place value, fraction representation, and the relationships between decimals and fractions—is crucial for mastering this skill and applying it effectively in various contexts. By mastering this conversion, you open the door to a deeper understanding of numbers and their representation, a crucial building block for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Multiplying And Dividing Rational Calculator
Sep 16, 2025
-
Ft 2 To In 2
Sep 16, 2025
-
4 8 Is Equal To
Sep 16, 2025
-
Convert 43 Fahrenheit To Celsius
Sep 16, 2025
-
How Long Is 14000 Minutes
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What's 1.3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.