Whats 10 Percent Of 45
saludintensiva
Sep 16, 2025 · 6 min read
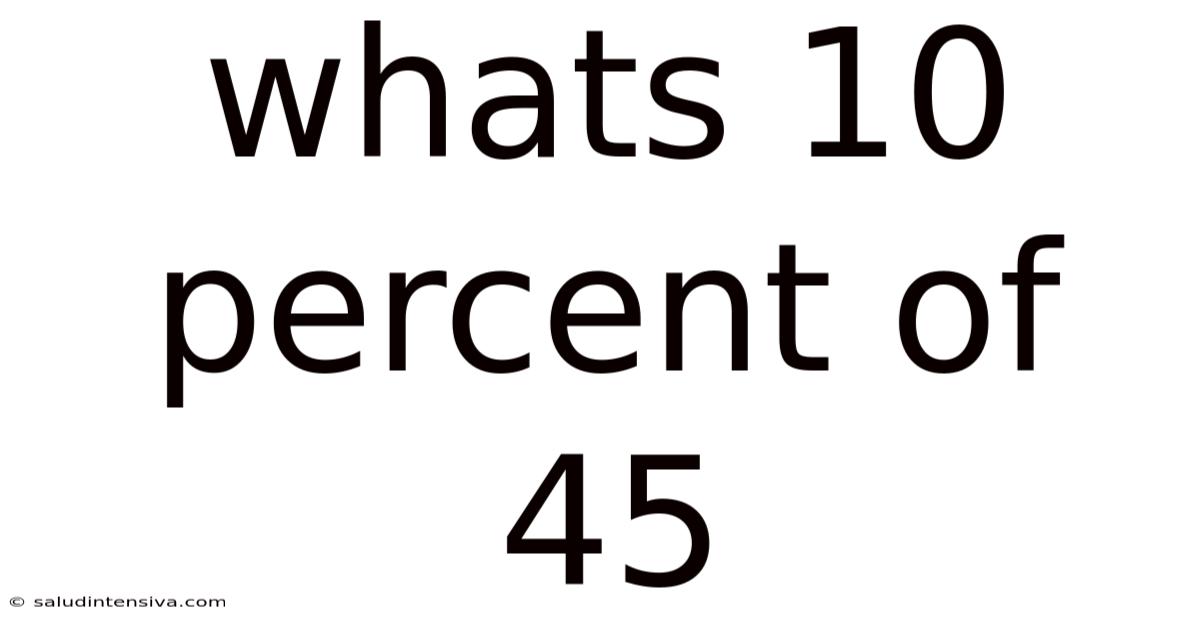
Table of Contents
What's 10 Percent of 45? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 45 might seem like a simple calculation, but it opens a door to understanding a fundamental concept in mathematics: percentages. This seemingly basic calculation underpins countless applications in everyday life, from calculating discounts and sales tax to understanding financial statements and statistical data. This article will not only answer the question "What's 10 percent of 45?" but will also explore the broader concept of percentages, offering various methods for calculation and showcasing their relevance in different contexts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental equivalence is crucial for calculating percentages.
Calculating 10 Percent of 45: Three Simple Methods
There are several ways to calculate 10% of 45. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. Since 10% is equivalent to 0.10, we simply multiply 45 by 0.10:
45 * 0.10 = 4.5
Therefore, 10% of 45 is 4.5.
Method 2: Using the Fraction Equivalent
As mentioned earlier, 10% can also be expressed as the fraction 10/100. This simplifies to 1/10. Therefore, to find 10% of 45, we can multiply 45 by 1/10:
45 * (1/10) = 45/10 = 4.5
Again, we arrive at the answer: 4.5.
Method 3: Finding 10% and Scaling Up
This method is particularly useful when dealing with larger percentages or numbers. We know that 1% of 45 is 45/100 = 0.45. Since 10% is ten times 1%, we simply multiply 0.45 by 10:
0.45 * 10 = 4.5
This method reinforces the concept of percentage as a fraction of 100.
Beyond the Basics: Calculating Other Percentages
While finding 10% of 45 is relatively simple, the same principles apply to calculating other percentages. Let's consider a few examples:
-
Finding 25% of 45: We can use the decimal equivalent (0.25) or the fraction (1/4). 45 * 0.25 = 11.25, or 45 * (1/4) = 11.25.
-
Finding 50% of 45: 50% is equivalent to 1/2, so 45 * (1/2) = 22.5. This also demonstrates that 50% is half the original number.
-
Finding 75% of 45: We can think of this as 50% + 25%, so 22.5 + 11.25 = 33.75. Alternatively, 75% is equivalent to 3/4, so 45 * (3/4) = 33.75.
-
Finding x% of y: The general formula is (x/100) * y. This formula allows you to calculate any percentage of any number.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill with numerous applications in various aspects of life:
-
Shopping: Calculating discounts, sales tax, and the final price after applying discounts. For example, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
-
Finance: Understanding interest rates on loans and investments, calculating returns on investments, analyzing financial statements, and budgeting. For example, a 5% interest rate on a $1000 loan means an interest payment of $50 per year.
-
Science and Statistics: Representing data in a clear and concise manner, making comparisons between different data sets, calculating probabilities, and analyzing statistical significance. Percentages are widely used in scientific research to report data and findings.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels (percentage of daily value), and even figuring out the percentage of tasks completed on a project.
Common Percentage Calculations and Shortcuts
Certain percentage calculations occur frequently, and knowing shortcuts can save time and effort:
-
10%: Move the decimal point one place to the left. (e.g., 10% of 75 is 7.5)
-
50%: Divide the number by 2. (e.g., 50% of 120 is 60)
-
25%: Divide the number by 4. (e.g., 25% of 80 is 20)
-
1%: Divide the number by 100. (e.g., 1% of 200 is 2)
Mastering these shortcuts enhances calculation speed and efficiency.
Addressing Potential Confusion and Misconceptions
Sometimes, people get confused when dealing with percentages, particularly when multiple percentages are involved or when percentages are applied successively. For example, a 20% increase followed by a 20% decrease does not result in the original value. These scenarios require careful attention to the order of operations and the specific meaning of percentage increases and decreases.
Another common misconception is treating percentages as additive. For example, if a price increases by 10% and then by another 10%, the overall increase is not 20%, but slightly more due to the compounding effect.
Similarly, subtracting percentages is not always intuitive. If a price is reduced by 20% and then by 10%, the total reduction is not 30%, but a little less. These complexities highlight the importance of a strong understanding of percentage calculations to avoid misinterpretations.
Advanced Applications: Percentage Change and Compound Interest
Let's delve into two more advanced applications of percentage calculations:
Percentage Change: This refers to the relative change between an initial value and a final value, expressed as a percentage. The formula for percentage change is:
[(Final Value - Initial Value) / Initial Value] * 100%
For instance, if a stock price increases from $50 to $60, the percentage change is [(60-50)/50] * 100% = 20%.
Compound Interest: This is interest calculated on both the principal amount and accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is crucial for long-term financial planning and investment strategies.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest way often depends on the specific percentage. For 10%, move the decimal point one place to the left. For 50%, divide by two. For other percentages, using the decimal equivalent (percentage divided by 100) and multiplying is generally straightforward.
Q: How do I calculate a percentage increase or decrease?
A: Use the formula [(New Value - Old Value) / Old Value] * 100%. A positive result indicates an increase, while a negative result indicates a decrease.
Q: Can I use a calculator to calculate percentages?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation.
Q: What if I need to calculate a percentage of a percentage?
A: Calculate each percentage step-by-step. Don't simply add or subtract the percentages.
Q: Are there any online tools to help calculate percentages?
A: Yes, numerous online percentage calculators are available; however, understanding the underlying principles is more beneficial in the long run.
Conclusion
Calculating 10 percent of 45, while seemingly simple, unveils a world of mathematical concepts and practical applications. Understanding percentages is essential for navigating various aspects of daily life, from personal finance to professional endeavors. By mastering the different methods of percentage calculation and understanding their applications, you equip yourself with a valuable skill that will serve you well in various contexts. The ability to calculate percentages accurately and efficiently is not just a mathematical skill; it’s a key to making informed decisions in a data-driven world. Remember to practice regularly to build confidence and proficiency in this essential skill.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 54
Sep 17, 2025
-
Lcm Of 26 And 39
Sep 17, 2025
-
Gcf Of 27 And 30
Sep 17, 2025
-
Capacity Of A Gas Tank
Sep 17, 2025
-
Gcf Of 17 And 34
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.