Whats 15 Percent Of 50
saludintensiva
Sep 10, 2025 · 5 min read
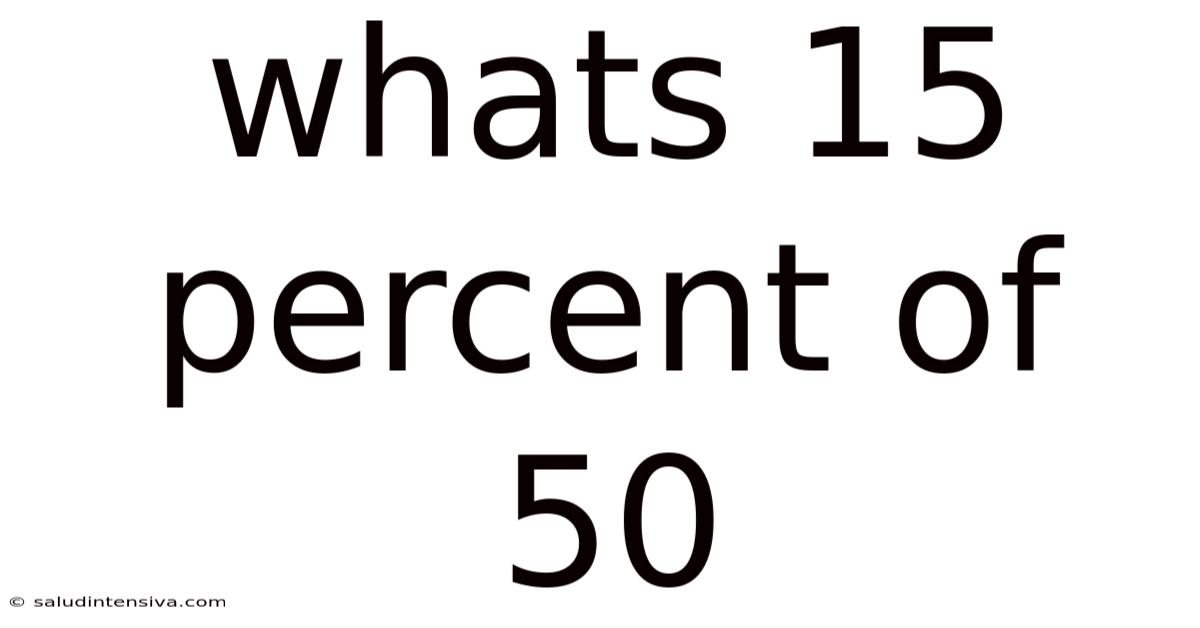
Table of Contents
What's 15 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 15% of 50 might seem like a simple calculation, but it opens a door to understanding the broader concept of percentages and their crucial role in various aspects of our lives. This article will not only answer the question directly but also delve into the underlying mathematical principles, explore different methods for calculating percentages, and demonstrate their practical applications in everyday situations. We'll also address common misconceptions and provide you with the tools to confidently tackle percentage problems of all complexities.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 15% means 15 out of 100, or 15/100. This fractional representation is fundamental to understanding and calculating percentages.
Method 1: The Direct Calculation Method
The most straightforward method to calculate 15% of 50 involves converting the percentage into a decimal and then multiplying it by the number.
-
Step 1: Convert the percentage to a decimal: To convert 15% to a decimal, divide it by 100: 15% / 100 = 0.15
-
Step 2: Multiply the decimal by the number: Multiply the decimal (0.15) by the number you're finding the percentage of (50): 0.15 x 50 = 7.5
Therefore, 15% of 50 is 7.5.
Method 2: Using Fractions
As mentioned earlier, percentages can be expressed as fractions. Let's use this approach to calculate 15% of 50.
-
Step 1: Convert the percentage to a fraction: 15% can be written as 15/100.
-
Step 2: Simplify the fraction (if possible): The fraction 15/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 5: 15/100 = 3/20
-
Step 3: Multiply the fraction by the number: Multiply the simplified fraction (3/20) by 50: (3/20) x 50 = 150/20
-
Step 4: Simplify the resulting fraction: 150/20 simplifies to 7.5
Again, we arrive at the answer: 15% of 50 is 7.5.
Method 3: The Proportion Method
This method utilizes the concept of proportions to solve percentage problems. We set up a proportion where one ratio represents the percentage (15/100) and the other represents the unknown value (x/50).
-
Step 1: Set up the proportion: 15/100 = x/50
-
Step 2: Cross-multiply: 15 x 50 = 100x
-
Step 3: Solve for x: 750 = 100x => x = 750/100 = 7.5
Once more, we find that 15% of 50 is 7.5.
Why Learn Different Methods?
While all three methods yield the same result, learning multiple approaches is beneficial for several reasons:
-
Flexibility: Different methods are more efficient depending on the specific problem. For simple calculations, the direct method might be quickest. For more complex problems involving fractions or ratios, the fraction or proportion method might be more intuitive.
-
Conceptual Understanding: Using various methods reinforces your understanding of percentages as fractions, decimals, and ratios, providing a holistic grasp of the concept.
-
Problem-Solving Skills: Exposure to different methods enhances your problem-solving skills, making you more adaptable to various mathematical challenges.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives, appearing in various contexts:
-
Finance: Calculating interest rates, discounts, taxes, tips, and investment returns. Understanding percentages is crucial for making informed financial decisions. For example, a 15% discount on a $50 item would save you $7.50.
-
Retail: Sales, discounts, and markups are all expressed as percentages. Consumers need to understand percentages to compare prices and make smart purchasing choices.
-
Science and Statistics: Percentages are used extensively in data analysis, scientific research, and statistical reporting to represent proportions and trends.
-
Education: Calculating grades, test scores, and performance metrics often involves percentages. Understanding percentages is essential for students to track their progress and identify areas for improvement.
-
Everyday Life: Determining percentages in recipes, calculating nutrition information, or understanding survey results all involve the use of percentages.
Common Misconceptions about Percentages
Several common misconceptions surround percentages:
-
Adding percentages directly: It's incorrect to simply add percentages without considering the base value. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting percentage changes: Percentage changes must always be relative to a base value. A percentage increase or decrease is always relative to the starting amount, not the final amount.
-
Confusing percentage points with percentage changes: A change of 10 percentage points is different from a 10% change. For instance, an increase from 20% to 30% is a 10-percentage-point increase, but a 50% increase (10/20).
Frequently Asked Questions (FAQ)
- Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, then divide the difference by the original value and multiply by 100. For a percentage decrease, follow the same process but subtract the new value from the original value.
- Q: How do I find what percentage one number is of another?
A: Divide the first number by the second number, and then multiply the result by 100.
- Q: What are some online calculators or tools available to help with percentage calculations?
A: Many free online percentage calculators are available. These tools can be helpful for quick calculations or for verifying your work. However, understanding the underlying principles is more valuable in the long run.
Conclusion
Calculating 15% of 50, as we've shown, is a simple yet illustrative example of percentage calculations. Understanding percentages is a fundamental skill applicable across numerous fields. By mastering different calculation methods and understanding the underlying concepts, you equip yourself with a valuable tool for navigating the quantitative aspects of daily life and professional endeavors. The ability to confidently work with percentages not only improves your problem-solving abilities but also empowers you to make informed decisions in various contexts, from personal finance to scientific analysis. Remember the different methods, avoid common pitfalls, and practice regularly to solidify your understanding and build confidence in tackling percentage problems of all kinds.
Latest Posts
Latest Posts
-
38 40 As A Percent
Sep 10, 2025
-
Half Of 3 1 2 Inches
Sep 10, 2025
-
1 4 As A Whole Number
Sep 10, 2025
-
One Million In Scientific Notation
Sep 10, 2025
-
Lateral Area Formula For Cylinder
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 15 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.