Whats 20 Percent Of 13
saludintensiva
Sep 17, 2025 · 5 min read
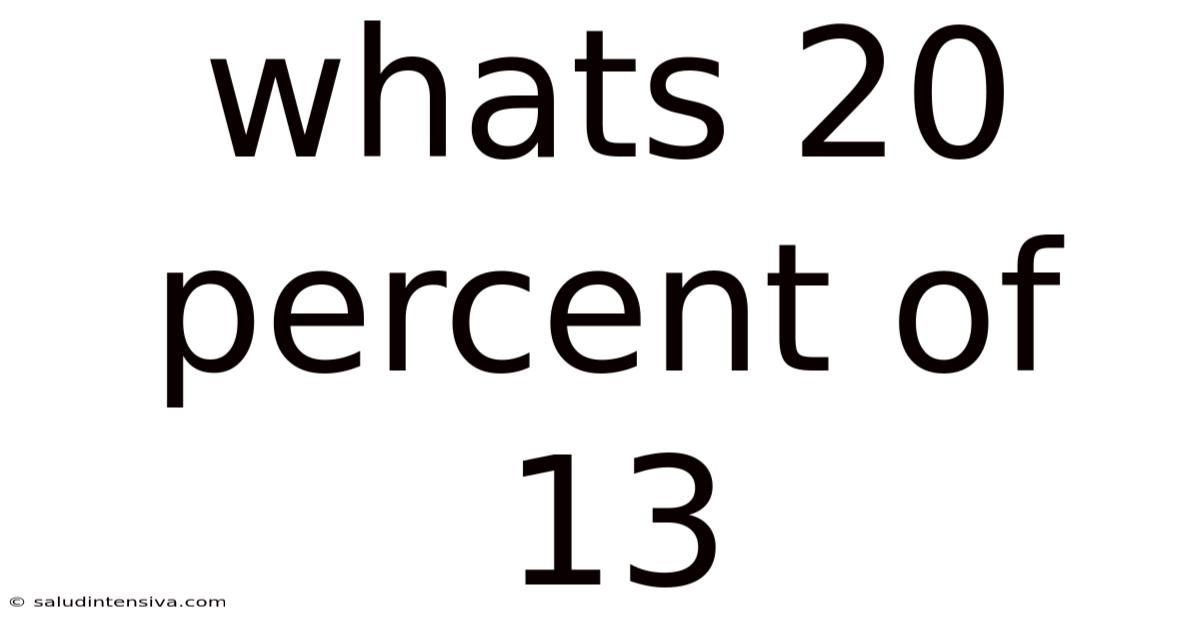
Table of Contents
What's 20 Percent of 13? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 13 might seem like a simple calculation, a quick task easily handled by a calculator. But understanding the underlying principles behind percentage calculations opens up a world of practical applications, from calculating discounts in a store to understanding complex financial data. This article will not only answer the question "What's 20 percent of 13?" but will also delve into the methods, the math behind it, and explore the broader context of percentages in everyday life.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20 percent (written as 20%) means 20 out of 100, or 20/100. This can be simplified to 1/5. This foundational understanding is crucial for any percentage calculation.
Method 1: Using the Decimal Equivalent
The most straightforward method to calculate 20 percent of 13 is to convert the percentage to its decimal equivalent. To do this, divide the percentage by 100. So, 20% becomes 20/100 = 0.20.
Now, multiply this decimal by the number you want to find the percentage of (13 in this case):
0.20 x 13 = 2.6
Therefore, 20 percent of 13 is 2.6.
Method 2: Using Fractions
As mentioned earlier, 20% can be expressed as the fraction 1/5. This method involves multiplying the fraction by the number:
(1/5) x 13 = 13/5
Now, simply divide 13 by 5:
13 ÷ 5 = 2.6
Again, we arrive at the answer: 20 percent of 13 is 2.6.
Method 3: Proportion Method
This method uses proportions to solve the problem. We set up a proportion where 'x' represents the unknown value (20% of 13):
20/100 = x/13
To solve for 'x', we cross-multiply:
20 x 13 = 100 x x
260 = 100x
Now, divide both sides by 100:
x = 260/100 = 2.6
This confirms once more that 20 percent of 13 is 2.6.
Choosing the Right Method
While all three methods yield the same correct answer, the best method depends on personal preference and the complexity of the problem. The decimal method is generally the quickest and easiest for simple calculations like this one. The fraction method is useful when dealing with easily simplifiable percentages, while the proportion method is a more versatile approach applicable to a wider range of percentage problems.
Practical Applications of Percentage Calculations
Understanding percentage calculations is far more than just an academic exercise. It's a crucial skill applied across numerous aspects of daily life and various professional fields:
-
Shopping and Discounts: Calculating discounts on sale items is a prime example. If a store offers a 20% discount on an item priced at $13, you'd use the percentage calculation to determine the discount amount ($2.60) and the final price ($10.40).
-
Taxes and Gratuities: Calculating sales tax or service charges (like tips in restaurants) involves percentage calculations. For instance, if the sales tax is 6%, you'd calculate 6% of the item's price to determine the tax amount.
-
Finance and Investments: Percentages are fundamental to understanding interest rates, returns on investments, and loan repayments. For example, annual interest rates on savings accounts or loans are expressed as percentages.
-
Data Analysis and Statistics: Percentages are extensively used in statistics to represent proportions, trends, and probabilities. Data analysis often involves calculating percentages to present findings in a clear and concise manner.
-
Science and Engineering: Percentage calculations are employed in various scientific and engineering applications, such as expressing the concentration of solutions, efficiency of processes, or error margins in measurements.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% of 13 is relatively simple, the principles extend to more complex scenarios. Consider these examples:
-
Finding the percentage increase or decrease: If a quantity increases from 10 to 13, the percentage increase is calculated as follows: [(13-10)/10] x 100% = 30%.
-
Calculating the original value given a percentage: If an item is discounted by 20% and costs $10.40, the original price can be calculated using the following method: Let 'x' be the original price. Then, 0.8x = $10.40. Solving for 'x', we get x = $13.
-
Working with multiple percentages: If you need to calculate multiple successive discounts or increases, it's crucial to apply the percentages sequentially rather than simply adding them. For example, a 10% discount followed by a 20% discount on a $100 item doesn't equal a 30% discount.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when working with percentages?
A: One common mistake is adding percentages directly without considering the base value. Another mistake is confusing percentage increase with percentage points. For instance, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Q: Are there any online tools or calculators that can help with percentage calculations?
A: Yes, many online calculators and tools are available to assist with percentage calculations. These tools can be especially helpful for more complex problems.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various percentage problems, starting with simple examples and gradually moving to more complex ones. You can find plenty of practice problems online or in textbooks. Understanding the underlying concepts of fractions and decimals is also crucial for mastering percentage calculations.
Conclusion
Calculating 20 percent of 13 is a straightforward task, easily solved using various methods. However, the underlying principles of percentage calculations have wide-ranging applications in numerous areas of life. Mastering percentage calculations is a valuable skill that enhances problem-solving capabilities and provides a stronger understanding of various quantitative concepts in both academic and practical contexts. By grasping the fundamental concepts and practicing regularly, you can build confidence and proficiency in handling a variety of percentage-based problems, empowering you to navigate the numerical world with greater ease and understanding. Remember, the key is to understand the underlying principles, not just the rote memorization of formulas. With consistent practice and a clear understanding of the concepts, percentages will become a simple and manageable tool in your everyday life.
Latest Posts
Latest Posts
-
13 As A Fraction Simplified
Sep 17, 2025
-
Lcm Of 18 And 20
Sep 17, 2025
-
Convert 250 Pounds To Kilos
Sep 17, 2025
-
260 Billion In Scientific Notation
Sep 17, 2025
-
Answer To A Multiplication Problem
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.