Whats 20 Percent Of 32
saludintensiva
Sep 21, 2025 · 5 min read
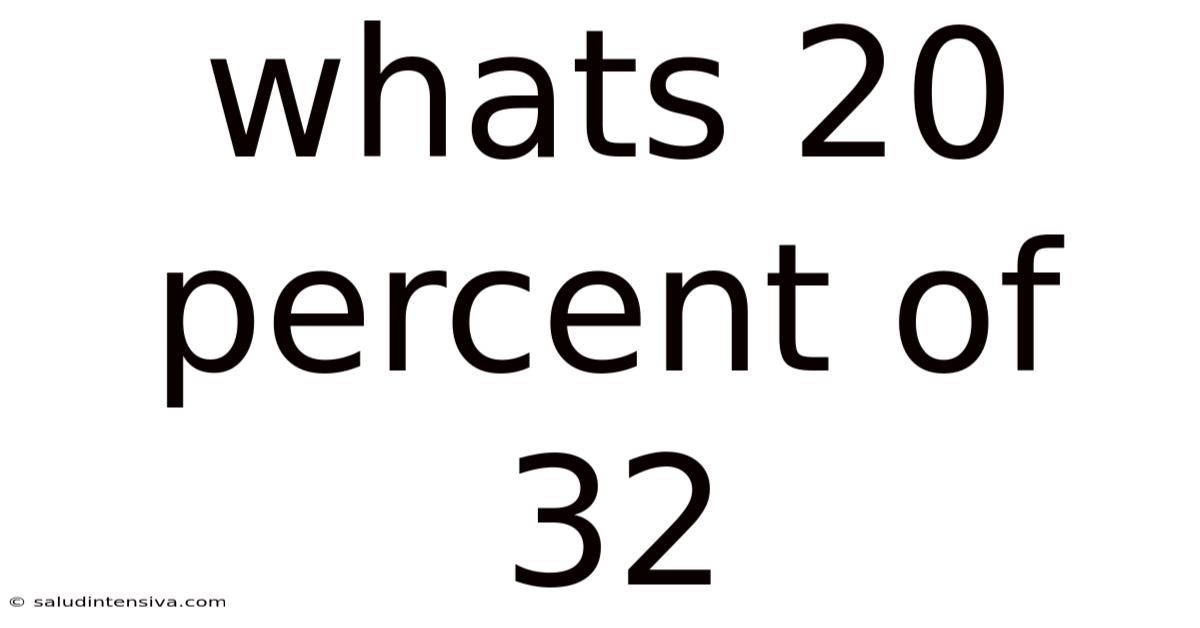
Table of Contents
What's 20 Percent of 32? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 32 might seem like a simple calculation, a quick task for a calculator. But this seemingly straightforward question opens a door to understanding a fundamental concept in mathematics: percentages. This article will not only answer the question directly but also explore the various methods to calculate percentages, their real-world applications, and delve into the underlying mathematical principles. We'll cover everything from basic arithmetic to more advanced percentage-related problems, ensuring a comprehensive understanding for readers of all levels.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). So, 20 percent (written as 20%) means 20 out of 100, or 20/100, which simplifies to 1/5. This fundamental understanding is crucial for tackling any percentage problem.
Method 1: Using the Fraction Method
The most intuitive way to calculate 20% of 32 is to convert the percentage to a fraction and then multiply.
- Step 1: Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Step 2: Multiply the fraction by the number: (1/5) * 32 = 32/5
- Step 3: Simplify the fraction or convert to a decimal: 32/5 = 6.4
Therefore, 20% of 32 is 6.4.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying.
- Step 1: Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Step 2: Multiply the decimal by the number: 0.20 * 32 = 6.4
Again, we arrive at the answer: 20% of 32 is 6.4. This method is often preferred for its simplicity and ease of use with calculators.
Method 3: Using the Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where 'x' represents the unknown value (20% of 32):
- 20/100 = x/32
To solve for 'x', we cross-multiply:
- 20 * 32 = 100 * x
- 640 = 100x
- x = 640/100
- x = 6.4
This method reinforces the understanding of percentages as ratios.
Real-World Applications of Percentages
Percentages are ubiquitous in everyday life, appearing in various contexts:
- Sales and Discounts: Retailers often advertise discounts as percentages (e.g., "20% off"). Understanding percentages is crucial for determining the actual price after a discount.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the total amount.
- Finance: Interest rates on loans and savings accounts are expressed as percentages. Understanding compound interest, which involves repeated percentage calculations, is vital for financial planning.
- Statistics and Data Analysis: Percentages are used extensively to represent proportions and trends in data. For example, survey results are often presented as percentages.
- Science: Percentages are frequently used in scientific calculations and experiments, particularly in areas like chemistry and biology. Concentration of solutions, for instance, is often expressed as a percentage.
Solving More Complex Percentage Problems
While finding 20% of 32 is a relatively simple calculation, the principles can be extended to more complex problems. Let's consider a few examples:
-
Finding the original amount: If 20% of a number is 6.4, what is the original number? This requires reversing the percentage calculation. We can set up the equation: 0.20 * x = 6.4. Solving for x, we get x = 6.4 / 0.20 = 32.
-
Calculating percentage increase or decrease: If a price increases from 32 to 40, what is the percentage increase? First, find the difference: 40 - 32 = 8. Then, divide the difference by the original amount and multiply by 100: (8/32) * 100 = 25%. The price increased by 25%.
-
Calculating percentage points: Note the difference between percentage change and percentage points. If interest rates rise from 5% to 10%, this is a 5 percentage point increase, but a 100% increase in the interest rate itself.
Percentage Calculations in Different Contexts
The application of percentages extends beyond simple calculations. Here are some advanced scenarios:
-
Compound Interest: This involves applying the interest rate to the principal amount plus accumulated interest over multiple periods. The formula for compound interest is A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
-
Percentage Yield in Chemistry: In chemistry, percentage yield refers to the ratio of the actual yield of a reaction to the theoretical yield, multiplied by 100. It represents the efficiency of a chemical reaction.
-
Statistical Significance: In statistics, percentages are used to determine the statistical significance of results. P-values, often expressed as percentages, indicate the probability of obtaining the observed results if there is no real effect.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages? A: The decimal method is generally the quickest and easiest for most people. Convert the percentage to a decimal and multiply.
-
Q: Can I use a calculator for percentage calculations? A: Absolutely! Calculators have percentage functions that make calculations much faster and more accurate.
-
Q: What if I need to calculate a percentage of a percentage? A: You simply multiply the percentages together (after converting them to decimals). For example, 10% of 20% is 0.10 * 0.20 = 0.02 or 2%.
-
Q: How do I deal with percentages greater than 100%? A: This simply means that the resulting value is more than the original amount. For example, 150% of 32 is 1.50 * 32 = 48.
-
Q: Are there any online tools to calculate percentages? A: Yes, many websites and apps offer percentage calculators that can handle various types of percentage problems.
Conclusion
While the answer to "What's 20 percent of 32?" is a straightforward 6.4, the underlying concept of percentages is far-reaching and essential for numerous applications in everyday life, finance, science, and more. Understanding the different methods for calculating percentages, from using fractions and decimals to solving proportions and tackling more complex problems, empowers individuals to confidently navigate the world of numbers and data. Mastering percentages is a crucial skill that enhances problem-solving abilities and contributes to a more comprehensive understanding of the quantitative aspects of the world around us. This understanding forms the basis for more complex mathematical concepts and applications, making it a foundational skill for learners of all ages and backgrounds. Continued practice and exposure to different percentage-related problems will solidify this crucial understanding and enhance its application in a variety of contexts.
Latest Posts
Latest Posts
-
Convert 125 Km To Miles
Sep 21, 2025
-
Barrels In A Cubic Meter
Sep 21, 2025
-
Is A Meter A Yard
Sep 21, 2025
-
15 3 5 Of 250
Sep 21, 2025
-
Days Until June 18 2024
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.