Whats 25 Percent Of 125
saludintensiva
Sep 11, 2025 · 5 min read
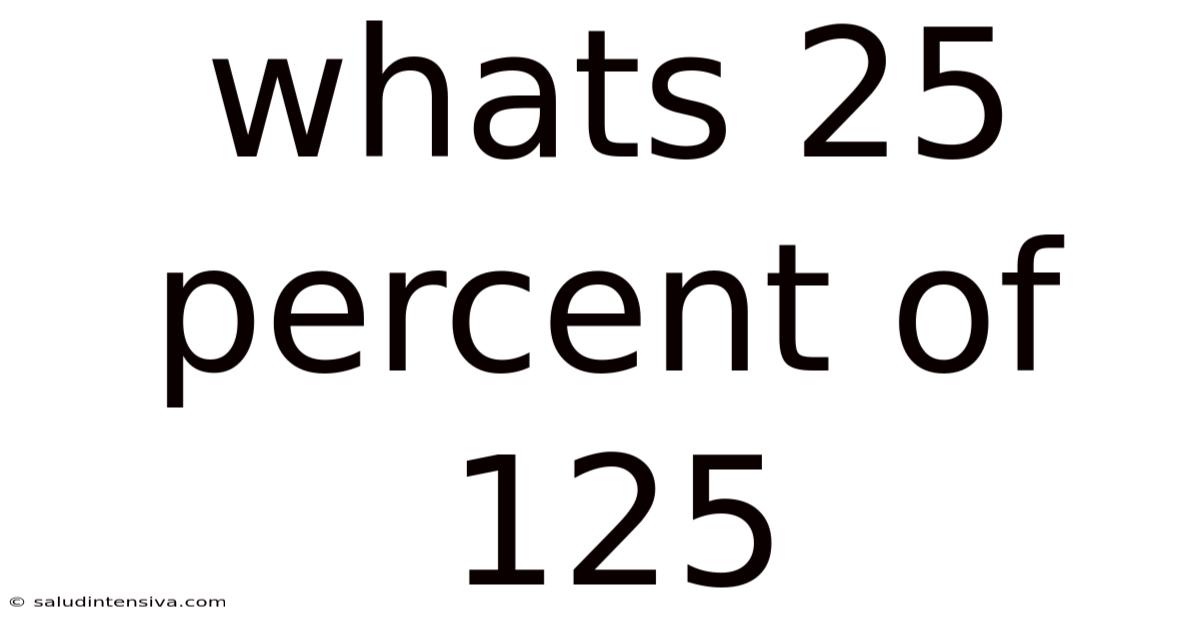
Table of Contents
What's 25 Percent of 125? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 125 might seem like a simple calculation, a quick problem for a middle schooler. But beneath the surface lies a world of mathematical concepts with broad applications in everyday life, from calculating discounts in a store to understanding financial growth. This article will not only solve this specific problem but also explore the underlying principles of percentages, offering multiple methods of calculation and demonstrating their real-world relevance. We'll delve into the intricacies of percentage calculations, offering insights that extend far beyond this single question.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." So, 25 percent (25%) means 25 out of 100, or 25/100, which simplifies to 1/4. This fundamental understanding is key to solving any percentage problem.
Method 1: Using the Fraction Method
This method leverages the fractional equivalent of a percentage. As established, 25% is equal to 1/4. Therefore, finding 25% of 125 is equivalent to finding 1/4 of 125.
- Calculation: (1/4) * 125 = 125/4 = 31.25
Therefore, 25% of 125 is 31.25.
Method 2: Using Decimal Conversion
Percentages can be easily converted to decimals by dividing the percentage by 100. In this case:
- Conversion: 25% / 100 = 0.25
Now, multiply this decimal by the number you're finding the percentage of:
- Calculation: 0.25 * 125 = 31.25
Again, we arrive at the answer: 25% of 125 is 31.25.
Method 3: Using Proportions
Proportions offer a powerful and versatile method for solving percentage problems. We can set up a proportion to represent the relationship between the percentage, the whole number, and the unknown part:
- Proportion: 25/100 = x/125
Where 'x' represents the unknown value (25% of 125). To solve for x, we cross-multiply:
-
Cross-multiplication: 25 * 125 = 100 * x
-
Simplification: 3125 = 100x
-
Solving for x: x = 3125 / 100 = 31.25
Thus, using proportions, we confirm that 25% of 125 is 31.25.
Beyond the Calculation: Real-World Applications
The seemingly simple calculation of "What's 25 percent of 125?" has far-reaching applications in numerous real-world scenarios:
-
Retail Discounts: Imagine a $125 item is on sale with a 25% discount. Using our calculations, the discount amount is $31.25, making the final price $93.75. This is a fundamental calculation for consumers understanding sales and promotions.
-
Financial Calculations: Percentage calculations are crucial in finance. Calculating interest earned on savings, understanding loan repayments, or determining investment returns all rely on understanding and applying percentages. A 25% increase in investment value, for instance, could dramatically change financial planning.
-
Data Analysis & Statistics: Percentages are fundamental in expressing data in a readily understandable format. In surveys, for example, results are often presented as percentages to show proportions of different responses within a sample population. Understanding percentages is therefore crucial for interpreting statistical data.
-
Scientific Measurements & Conversions: Percentages are also used extensively in scientific contexts. Expressing concentration of solutions, measuring error margins in experiments, or even expressing changes in physical quantities over time often utilizes percentage calculations.
-
Taxes and Tips: Calculating sales tax, calculating tips at a restaurant, or understanding income tax deductions all require a firm grasp of percentages. A 25% tip on a $125 bill, for example, would be $31.25.
Understanding Percentage Increase and Decrease
While we've focused on finding a percentage of a number, it's also important to understand percentage increase and decrease. This is often seen in contexts like:
-
Price Increases: A 25% price increase on a $125 item would be calculated as: (25/100) * 125 = $31.25 increase. The new price would be $125 + $31.25 = $156.25
-
Price Decreases (Discounts): A 25% price decrease (discount) on a $125 item would be calculated as: (25/100) * 125 = $31.25 decrease. The new price would be $125 - $31.25 = $93.75
-
Population Growth/Decline: Percentages are commonly used to represent changes in population sizes. A 25% increase in a town's population of 125 would mean an additional 31.25 people. Note that in real-world situations, populations are represented by whole numbers, so you would round the result appropriately.
Advanced Applications and Further Exploration
The applications of percentage calculations extend to more complex scenarios including:
-
Compound Interest: This involves earning interest on both the principal amount and accumulated interest. It's a crucial concept in long-term investments and loans.
-
Statistical Significance: In statistical analysis, percentages help determine if observed differences between groups are significant or merely due to chance.
-
Financial Modeling: Percentages are essential in building financial models to predict future outcomes, analyze risks, and make informed investment decisions.
-
Rate of Change: Calculating the percentage change between two values helps understand trends and patterns over time.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage of a number without a calculator?
- A: You can use the fraction method or the proportion method. The fraction method is often easiest for common percentages like 25%, 50%, and 75%. The proportion method allows you to solve for any percentage.
-
Q: What if I need to find a percentage that's not a whole number, like 22.5%?
- A: Use the decimal conversion method. Convert 22.5% to 0.225 and multiply by the number.
-
Q: How do I reverse a percentage change?
- A: To find the original value after a percentage increase or decrease, you'll need to use algebraic equations. For example, if a price increased by 25% to $156.25, you would solve the equation: x + 0.25x = 156.25 This simplifies to 1.25x = 156.25, and solving for x gives you the original price.
Conclusion
While the initial question, "What's 25 percent of 125?", might seem straightforward, this article has demonstrated the depth and breadth of percentage calculations and their importance in various fields. Mastering percentage calculations is a fundamental skill with applications spanning daily life, finance, science, and beyond. By understanding the underlying principles and the various methods of calculation, you're equipped to confidently tackle a wide range of percentage problems and leverage this knowledge to make informed decisions in diverse contexts. Remember, the ability to understand and work with percentages is a valuable tool for navigating the complexities of the modern world.
Latest Posts
Latest Posts
-
Gcf For 12 And 28
Sep 11, 2025
-
90 Days From 6 19
Sep 11, 2025
-
Equivalent Fractions To 8 10
Sep 11, 2025
-
Gcf Of 50 And 30
Sep 11, 2025
-
4 5 8 As A Decimal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.