Whats 25 Percent Of 60
saludintensiva
Sep 19, 2025 · 5 min read
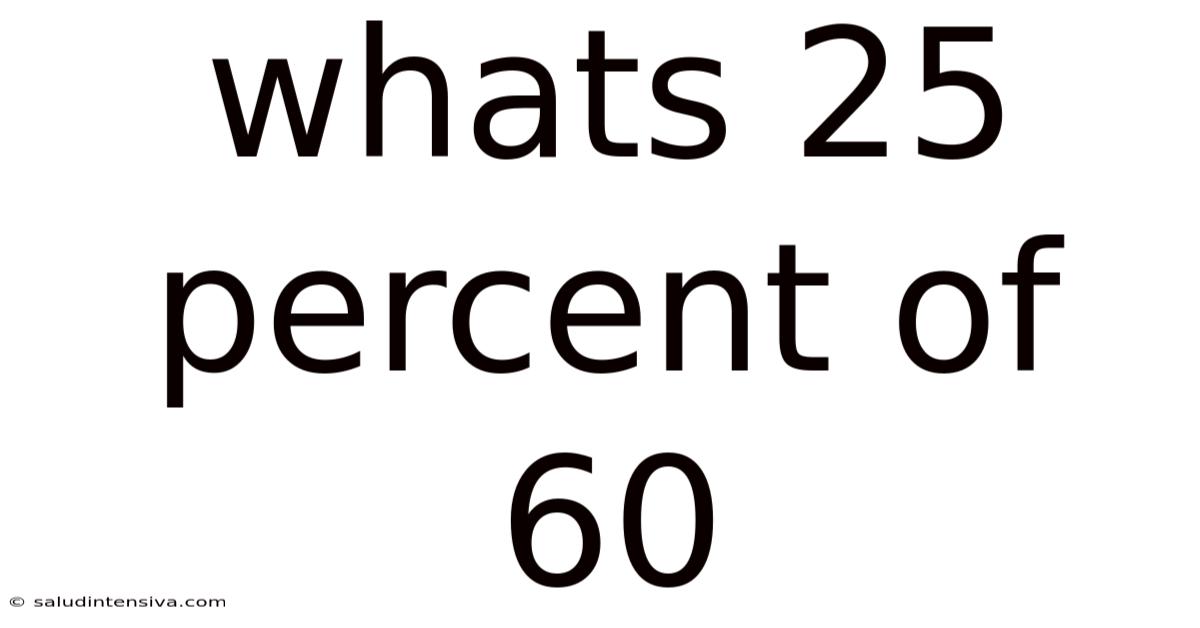
Table of Contents
What's 25 Percent of 60? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 60 might seem like a simple calculation, but it opens a door to understanding a fundamental concept in mathematics: percentages. This seemingly basic question actually underpins a wide range of applications in everyday life, from calculating discounts and sales tax to understanding financial reports and interpreting statistical data. This article will not only answer the question "What's 25 percent of 60?" but also explore the underlying principles, provide multiple methods for solving percentage problems, and discuss real-world examples where this type of calculation is essential.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." So, 25 percent (25%) means 25 out of 100, or 25/100. This can be simplified to the fraction 1/4. Understanding this fundamental relationship is key to solving percentage problems.
Method 1: Using the Fraction Method
The easiest way to calculate 25% of 60 is to leverage the fractional equivalent of 25%. As we established, 25% is equal to 1/4. Therefore, finding 25% of 60 is the same as finding 1/4 of 60. This is a simple division problem:
60 ÷ 4 = 15
Therefore, 25% of 60 is 15.
Method 2: Converting Percentage to Decimal
Another common method involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. For 25%, this would be:
25 ÷ 100 = 0.25
Then, multiply this decimal by the number you're finding the percentage of:
0.25 × 60 = 15
Again, we arrive at the answer: 25% of 60 is 15.
Method 3: Using Proportions
Proportions offer a more versatile method, especially useful for more complex percentage problems. A proportion sets up an equivalence between two ratios. We can set up a proportion like this:
x / 60 = 25 / 100
Where 'x' represents the unknown value (25% of 60). To solve for 'x', we cross-multiply:
100x = 25 × 60
100x = 1500
x = 1500 ÷ 100
x = 15
Once again, the answer is: 25% of 60 is 15.
Beyond the Basics: Applications of Percentage Calculations
The seemingly simple calculation of 25% of 60 has far-reaching applications in various fields. Let's explore some real-world examples:
-
Retail Discounts: Imagine a store offering a 25% discount on an item priced at $60. Using the methods described above, you would quickly calculate the discount as $15, meaning the final price would be $60 - $15 = $45. This is a common calculation shoppers make daily.
-
Sales Tax: Conversely, sales tax calculations involve percentages. If the sales tax rate is 25% (though this is a high rate in most places!), then the tax on a $60 item would be $15.
-
Financial Literacy: Understanding percentages is crucial for managing personal finances. Calculating interest rates on loans or savings accounts, understanding investment returns, and analyzing budgets all rely heavily on percentage calculations. For example, if your investment grows by 25% and you invested $60, your profit would be $15.
-
Statistics and Data Analysis: Percentages are essential for interpreting statistical data. For instance, representing survey results, expressing population growth rates, or illustrating market share often uses percentages. If 25% of a survey's 60 participants chose a particular option, it means 15 participants made that choice.
-
Science and Engineering: Percentage calculations are frequently used in scientific experiments and engineering designs to express ratios, concentrations, and efficiencies. For example, calculating the percentage yield in a chemical reaction or expressing the efficiency of a machine relies on percentage calculations.
Advanced Percentage Problems and Solving Strategies
While finding 25% of 60 is relatively straightforward, more complex scenarios might require a different approach. Here are some advanced scenarios and how to tackle them:
- Finding the original value: Let's say you bought an item after a 25% discount and paid $45. To find the original price, you'd need to work backward. Since you paid 75% (100% - 25%) of the original price, you can set up a proportion:
45 / x = 75 / 100
Solving for x (the original price), you would find x = $60.
-
Calculating percentage increase or decrease: Suppose a value increased from 60 to 75. To calculate the percentage increase, first find the difference (75 - 60 = 15). Then, divide this difference by the original value (15 / 60 = 0.25) and multiply by 100 to express it as a percentage (0.25 × 100 = 25%). Therefore, the value increased by 25%. Similar calculations can determine percentage decrease.
-
Compound percentages: These involve applying percentages successively. For instance, if a value increases by 25% and then decreases by 25%, the final value will not be the same as the original. These calculations require careful step-by-step application of percentage changes.
Frequently Asked Questions (FAQ)
-
Q: Are there any shortcuts for calculating percentages?
- A: Yes, for certain percentages like 10%, 25%, 50%, and 75%, you can use their fractional equivalents for quicker calculations. Also, many calculators have built-in percentage functions.
-
Q: What if I need to calculate a percentage of a decimal number?
- A: The methods remain the same. Convert the percentage to a decimal and multiply by the decimal number.
-
Q: How can I improve my skills in calculating percentages?
- A: Practice is key! Start with simple problems and gradually work your way up to more complex scenarios. Use online calculators and worksheets to test your understanding.
-
Q: Are there any online tools or calculators to help with percentage calculations?
- A: Yes, many free online calculators are available that can quickly compute percentages.
Conclusion
While the answer to "What's 25 percent of 60?" is simply 15, the journey to find that answer reveals the importance and wide-ranging applications of percentage calculations in various aspects of life. Mastering percentage calculations is a valuable skill that enhances your understanding of financial matters, data analysis, and various other fields. By understanding the different methods and practicing regularly, you can confidently tackle even the most complex percentage problems. Remember that the foundation lies in understanding the basic concept of percentages as parts of 100 and choosing the most efficient method based on the specific problem at hand.
Latest Posts
Latest Posts
-
Convert Sq Feet To Inches
Sep 19, 2025
-
Can 9 16 Be Simplified
Sep 19, 2025
-
How Long Is 150 Minutes
Sep 19, 2025
-
9 20 To A Decimal
Sep 19, 2025
-
15 32 As A Decimal
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.