Whats Bigger 3/8 Or 7/16
saludintensiva
Sep 14, 2025 · 6 min read
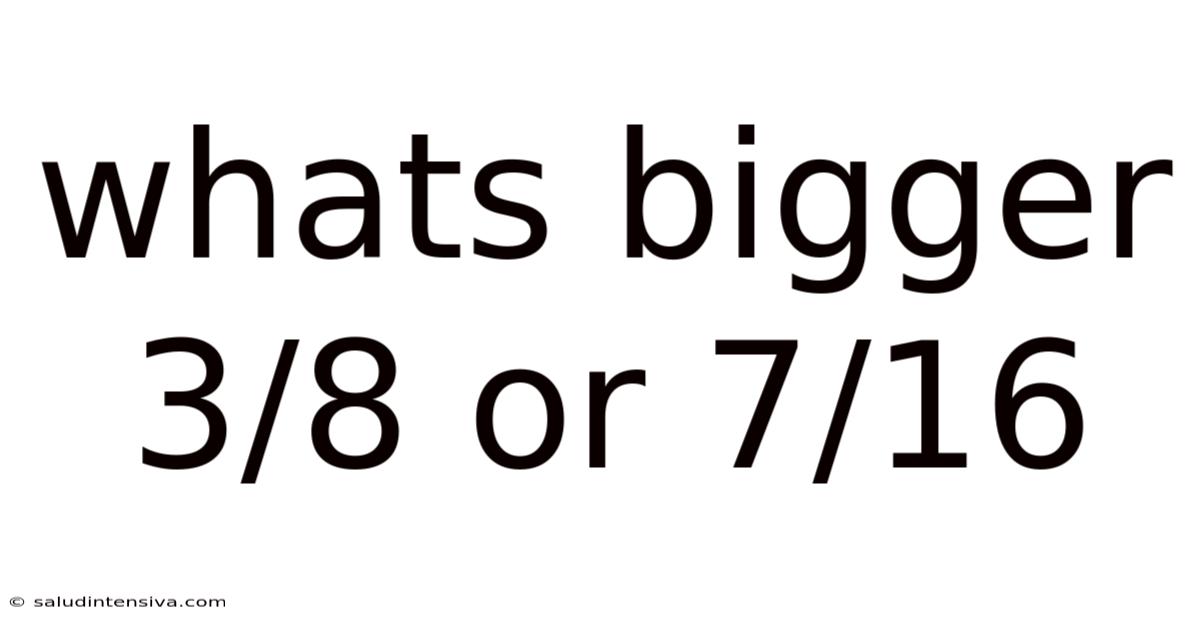
Table of Contents
What's Bigger: 3/8 or 7/16? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. Often, we encounter situations where we need to compare fractions to determine which is larger or smaller. This article will thoroughly explore the comparison of 3/8 and 7/16, providing not just the answer but also a deep understanding of the methods involved, equipping you with the tools to confidently tackle similar comparisons in the future. We'll cover multiple approaches, including visual representations, equivalent fractions, and decimal conversions.
Introduction: Understanding Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator, which is the top number, indicating the number of parts we have; and the denominator, which is the bottom number, indicating the total number of equal parts the whole is divided into. For instance, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts.
Method 1: Visual Representation
A helpful way to compare fractions is through visual representation. Imagine two identical pizzas. Let's divide the first pizza into 8 equal slices and shade 3 of them (representing 3/8). Now, divide the second pizza into 16 equal slices and shade 7 of them (representing 7/16). By visually comparing the shaded areas, you'll quickly observe that the pizza representing 7/16 has a larger shaded area than the pizza representing 3/8. Therefore, 7/16 is bigger than 3/8.
Method 2: Finding a Common Denominator
This is a more formal mathematical method. To compare fractions with different denominators, we need to find a common denominator – a number that is a multiple of both denominators. In our case, the denominators are 8 and 16. Notice that 16 is a multiple of 8 (8 x 2 = 16). This makes 16 the least common denominator (LCD).
Now, let's convert both fractions to have a denominator of 16:
-
3/8: To change the denominator from 8 to 16, we multiply both the numerator and denominator by 2: (3 x 2) / (8 x 2) = 6/16
-
7/16: This fraction already has a denominator of 16, so it remains unchanged.
Now we have 6/16 and 7/16. Since both fractions have the same denominator, we can directly compare their numerators. 7 is greater than 6, therefore, 7/16 is greater than 6/16, and consequently, 7/16 is greater than 3/8.
Method 3: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
-
3/8: 3 ÷ 8 = 0.375
-
7/16: 7 ÷ 16 = 0.4375
Comparing the decimal values, 0.4375 is greater than 0.375. Therefore, 7/16 is greater than 3/8.
Method 4: Cross-Multiplication
This method is a shortcut for comparing fractions. We cross-multiply the numerators and denominators.
-
Multiply the numerator of the first fraction (3) by the denominator of the second fraction (16): 3 x 16 = 48
-
Multiply the numerator of the second fraction (7) by the denominator of the first fraction (8): 7 x 8 = 56
Compare the results: 48 < 56. Since the result of the second multiplication (56) is greater, the second fraction (7/16) is greater.
Detailed Explanation: Why 7/16 is Larger
The fundamental reason why 7/16 is larger than 3/8 lies in the relative sizes of the parts. When we divide a whole into 16 equal parts, each part is smaller than when we divide the same whole into only 8 equal parts. However, we have 7 of these smaller parts in 7/16, which collectively represent a larger portion of the whole compared to having only 3 of the larger parts in 3/8. The common denominator method clearly illustrates this; by expressing both fractions with a denominator of 16, we directly compare the number of parts, revealing that 7 is more than 6.
Extending the Concept: Comparing More Complex Fractions
The methods described above – finding a common denominator, converting to decimals, and cross-multiplication – are universally applicable for comparing any two fractions, regardless of their complexity. The key is to choose the method that you find most comfortable and efficient. For instance, if you're dealing with fractions with larger numbers, converting to decimals might be quicker than finding the least common denominator.
Practical Applications: Real-World Examples
The ability to compare fractions is essential in many real-world situations:
-
Baking: A recipe might call for 3/8 cup of sugar in one part and 7/16 cup in another. Understanding which quantity is greater ensures accurate measurements.
-
Construction: In carpentry or other construction work, precise measurements are crucial. Comparing fractions helps in determining which piece of wood is longer or shorter.
-
Finance: Calculating portions of budgets or comparing interest rates often involves fraction comparison.
-
Data Analysis: In data analysis and statistics, understanding fraction comparison is essential for interpreting data and making informed decisions.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to tell which fraction is larger without calculations?
A: Not always. However, if the fractions have the same numerator, the fraction with the smaller denominator is larger (e.g., 2/3 > 2/5). If the fractions have the same denominator, the fraction with the larger numerator is larger (e.g., 5/8 > 3/8). But for fractions with different numerators and denominators, calculations are generally necessary.
Q: What if the fractions have very large numbers?
A: The methods remain the same. A calculator can assist with the calculations, especially when converting to decimals or finding the least common denominator.
Q: Can I always find a common denominator?
A: Yes, you can always find a common denominator for any two fractions. The least common denominator is the smallest number that is a multiple of both denominators. If you cannot easily find it, you can always multiply the two denominators together to get a common denominator (though it might not be the least common denominator).
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill with broad applications. This article provided multiple methods – visual representation, common denominator, decimal conversion, and cross-multiplication – to effectively compare fractions. Understanding these methods not only allows you to determine which fraction is larger but also cultivates a deeper understanding of fractional values and their representation. By mastering these techniques, you’ll be better equipped to tackle mathematical problems and real-world situations requiring fraction comparison with confidence and accuracy. Remember that consistent practice is key to solidifying your understanding and developing fluency in working with fractions. Don't hesitate to revisit these methods and try comparing different fractions to further enhance your skills.
Latest Posts
Latest Posts
-
3 4 Plus 1 3
Sep 14, 2025
-
Lcm Of 8 And 36
Sep 14, 2025
-
Lcm Of 90 And 60
Sep 14, 2025
-
The Amount Of Each Payment
Sep 14, 2025
-
60 Minutes In 1 Hour
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Whats Bigger 3/8 Or 7/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.