What's Equivalent To 2 4
saludintensiva
Sep 14, 2025 · 6 min read
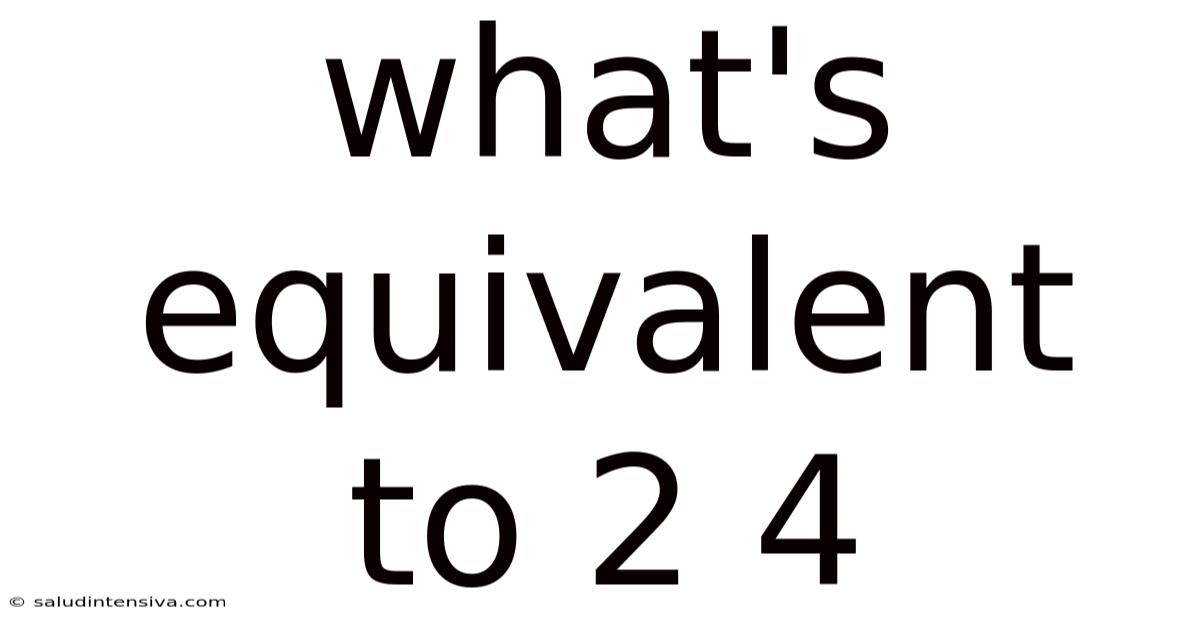
Table of Contents
What's Equivalent to 2⁴? Understanding Exponents and Their Applications
This article explores the mathematical concept of exponents, specifically focusing on the expression 2⁴ and its equivalent value. We'll delve into the meaning of exponents, demonstrate how to calculate 2⁴, and discuss its broader applications in various fields. Understanding exponents is crucial for anyone venturing into mathematics, science, or even finance, as it forms the basis of many complex calculations and concepts. This exploration will cover the fundamental principles, provide practical examples, and answer frequently asked questions, ensuring a comprehensive understanding of this important mathematical concept.
Understanding Exponents: The Power of Repeated Multiplication
In mathematics, an exponent (also known as a power or index) is a number that indicates how many times a base number is multiplied by itself. It's represented as a superscript number to the right of the base. For instance, in the expression a<sup>b</sup>, 'a' is the base and 'b' is the exponent. This indicates that 'a' is multiplied by itself 'b' times.
Let's break it down further with a few simple examples:
- 2²: This means 2 multiplied by itself twice: 2 x 2 = 4
- 3³: This means 3 multiplied by itself three times: 3 x 3 x 3 = 27
- 5¹: Any number raised to the power of 1 is simply itself: 5¹ = 5
- 10⁰: Any non-zero number raised to the power of 0 equals 1: 10⁰ = 1
Calculating 2⁴: Step-by-Step
Now, let's focus on the specific problem: what is the equivalent of 2⁴?
The expression 2⁴ indicates that the base number 2 is multiplied by itself four times. Therefore, the calculation is as follows:
2⁴ = 2 x 2 x 2 x 2 = 16
Therefore, the equivalent of 2⁴ is 16.
Beyond the Basics: Exploring Different Bases and Exponents
While we've focused on 2⁴, understanding exponents extends to various base numbers and exponents. Let's examine a few examples to broaden our understanding:
- 3⁵: This represents 3 x 3 x 3 x 3 x 3 = 243
- 10³: This represents 10 x 10 x 10 = 1000 (Notice the pattern: 10 raised to the power of 'n' results in 'n' number of zeros after 1).
- (1/2)²: This represents (1/2) x (1/2) = 1/4 (Exponents apply to fractions as well).
- (-2)³: This represents (-2) x (-2) x (-2) = -8 (Note the importance of parentheses – they ensure the negative sign is included in the multiplication).
These examples illustrate the versatility of exponents and their ability to represent repeated multiplication efficiently, regardless of the nature of the base.
Applications of Exponents: Real-World Uses
Exponents are far from being a purely abstract mathematical concept; they find practical applications across various fields. Here are some examples:
-
Compound Interest: In finance, compound interest calculations heavily rely on exponents. The formula for compound interest involves an exponent that represents the number of compounding periods. Understanding exponents is crucial for anyone seeking to understand how their savings or investments grow over time.
-
Scientific Notation: Exponents are essential in scientific notation, which is used to represent extremely large or small numbers concisely. For instance, the speed of light (approximately 300,000,000 meters per second) can be expressed in scientific notation as 3 x 10⁸ m/s.
-
Computer Science: Binary numbers (base-2), which are fundamental to computer systems, use exponents to represent values. Each digit in a binary number represents a power of 2.
-
Physics and Engineering: Exponential functions (functions where the variable appears as an exponent) are frequently used to model various physical phenomena, including radioactive decay, population growth, and the behavior of electrical circuits.
-
Data Analysis and Statistics: Exponential growth and decay models are used extensively in analyzing trends and making predictions in various fields like epidemiology, economics, and environmental science.
Understanding Negative and Fractional Exponents
The concept of exponents extends beyond positive integers. Negative and fractional exponents also have specific meanings:
-
Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive power. For example:
2⁻² = 1/2² = 1/4
a⁻ⁿ = 1/aⁿ
-
Fractional Exponents: A fractional exponent represents a combination of exponentiation and root extraction. For example:
2^(1/2) = √2 (the square root of 2)
a^(m/n) = ⁿ√(a)ᵐ (the nth root of a raised to the power of m)
Understanding negative and fractional exponents expands the range of problems that can be solved using this powerful mathematical tool.
Advanced Concepts Related to Exponents
Once the basics are understood, more complex concepts involving exponents can be explored. These include:
-
Logarithms: Logarithms are the inverse function of exponents. They help determine the exponent needed to obtain a particular value.
-
Exponential Functions and Equations: These are equations where the variable appears in the exponent. Solving exponential equations often requires utilizing logarithms.
-
Exponential Growth and Decay: These are models that describe how quantities change over time at a rate proportional to their current value. Examples include population growth, radioactive decay, and the cooling of objects.
Frequently Asked Questions (FAQs)
Q1: What is the difference between 2⁴ and 4²?
A1: While both involve exponents, they represent different calculations. 2⁴ (2 raised to the power of 4) is 2 x 2 x 2 x 2 = 16. 4² (4 raised to the power of 2) is 4 x 4 = 16. In this specific case, they yield the same result, but this is not always the case.
Q2: How can I calculate large exponents without a calculator?
A2: For large exponents, manual calculation becomes tedious. However, understanding the properties of exponents can simplify the process. For example, you can break down large exponents into smaller, more manageable parts. For instance, 2¹⁰ can be calculated as (2⁵)² = 32² = 1024.
Q3: Are there any tricks or shortcuts for calculating exponents?
A3: While there aren't universal shortcuts for all exponents, recognizing patterns and using properties of exponents (such as the power of a product or power of a quotient rules) can simplify calculations. Practice and familiarity with exponent rules are crucial for developing efficient calculation strategies.
Q4: Why are exponents important in real-world applications?
A4: Exponents provide a concise and efficient way to represent repeated multiplication. This efficiency is vital in various fields, from finance (compound interest) to science (scientific notation) and computer science (binary numbers). They are fundamental to understanding exponential growth and decay, which are crucial for modeling real-world phenomena.
Conclusion: Mastering the Power of Exponents
This comprehensive exploration of exponents, with a specific focus on 2⁴ and its equivalent value of 16, highlights the importance of this fundamental mathematical concept. From its straightforward application in calculating repeated multiplication to its advanced uses in various fields, understanding exponents is crucial for anyone seeking to deepen their mathematical understanding and its applications in the real world. By mastering the principles discussed here, you'll not only be able to solve problems involving exponents but also gain a clearer understanding of how they are used to model and explain complex phenomena in science, finance, and technology. Remember to practice consistently, explore various examples, and delve deeper into related concepts like logarithms and exponential functions to fully grasp the power of this essential mathematical tool.
Latest Posts
Latest Posts
-
Convert 625 Into A Fraction
Sep 14, 2025
-
Adding And Subtracting With Money
Sep 14, 2025
-
10 000 Psi To Bar
Sep 14, 2025
-
Is 1 8 Bigger Than 5 32
Sep 14, 2025
-
What Was 30 Weeks Ago
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What's Equivalent To 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.