X 1 6 2 3
saludintensiva
Sep 11, 2025 · 6 min read
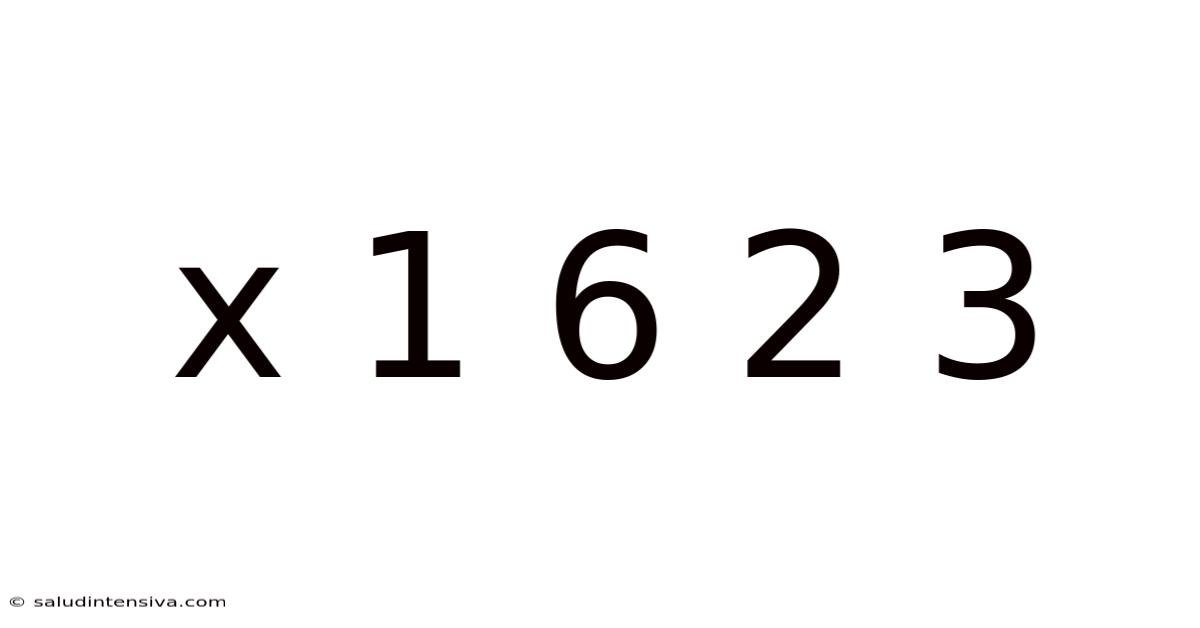
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Logical Possibilities of "x 1 6 2 3"
This article delves into the fascinating puzzle presented by the sequence "x 1 6 2 3". We'll explore various mathematical and logical approaches to determine the value of 'x', examining different patterns, rules, and possibilities. This seemingly simple sequence opens doors to a world of mathematical thinking and problem-solving strategies. Understanding how to approach this puzzle provides valuable insights into pattern recognition, logical deduction, and the beauty of mathematical exploration.
Introduction: The Allure of the Unknown
The sequence "x 1 6 2 3" immediately presents a challenge. The unknown variable 'x' acts as a hook, drawing us into a process of deduction and analysis. What underlying rule governs this sequence? Is there a single, definitive answer, or are multiple solutions possible? These are the questions we will address throughout this article. The seemingly simple nature of the sequence belies a surprising depth of potential solutions, making it a rich and rewarding subject for mathematical exploration.
Methodological Approaches: Unveiling the Patterns
To decipher the sequence, we need to systematically explore different mathematical and logical approaches. We can begin by considering various possibilities, from simple arithmetic progressions to more complex algorithms.
1. Arithmetic Progressions and Differences:
A common initial approach is to examine the differences between consecutive numbers. Let's calculate the differences between known elements:
- 1 - x = difference 1
- 6 - 1 = 5
- 2 - 6 = -4
- 3 - 2 = 1
The differences (5, -4, 1) don't immediately reveal a clear arithmetic progression. This suggests that a more complex rule might be at play. However, we can still use these differences to inform our hypotheses. For instance, if we assume a cyclical pattern within the differences themselves, we might find a solution. Alternatively, looking at the second differences (the differences between the differences) might uncover a hidden pattern.
2. Geometric Progressions and Ratios:
Another approach involves considering geometric progressions. Here, we would examine the ratios between consecutive numbers.
- 1/x = ratio 1
- 6/1 = 6
- 2/6 = 1/3
- 3/2 = 1.5
Again, the ratios don't immediately reveal a simple geometric progression. The absence of a clear arithmetic or geometric pattern points towards a more intricate relationship between the numbers.
3. Polynomial Functions:
We can also approach this problem using polynomial functions. A polynomial function of degree n will fit n+1 points. Since we have five points (including the unknown 'x'), we could potentially find a cubic polynomial (degree 3) that fits all the points. This involves solving a system of four equations with four unknowns (the coefficients of the cubic polynomial). However, this method might lead to multiple solutions, underscoring the need for additional constraints or assumptions.
4. Modular Arithmetic and Cyclic Patterns:
Modular arithmetic could be relevant if the sequence exhibits cyclical behavior. We might explore if the numbers show a repeating pattern when considered modulo n for different values of n. For example, looking at the sequence modulo 2, modulo 3, or modulo 5 might reveal underlying patterns. This approach often requires testing different moduli to find a consistent pattern.
5. Logical and Algorithmic Approaches:
Beyond purely mathematical approaches, we can consider logical or algorithmic rules. For example, there could be a rule based on the position of the numbers in the sequence. Perhaps the odd-numbered positions follow one rule, while the even-numbered positions follow another. Alternatively, the rule might be recursive, with each number depending on the preceding ones. This opens up the possibility of several valid algorithmic solutions.
6. Considering 'x' as a Parameter:
Instead of seeking a single value for 'x', we could treat it as a parameter. This would allow us to investigate how different values of 'x' impact the subsequent sequence elements and overall pattern. By varying 'x' and analyzing the resulting sequences, we can gain insights into the potential range of values and the nature of the governing rule.
Exploring Specific Scenarios and Potential Solutions:
Let's explore some possible scenarios and illustrate how different approaches might yield potential solutions. Remember, these are just examples, and other solutions are certainly possible depending on the underlying rules we assume.
Scenario 1: A Simple Recursive Rule
Let's assume a simple recursive rule where each number is derived from the previous one using a consistent operation. This wouldn't perfectly fit the given sequence, but it can illustrate the process.
Let's postulate that each number is obtained by adding a specific increment to the previous number, which itself changes. For instance:
- x + 5 = 1
- 1 + 5 = 6 (incorrect)
The simplicity of the pattern must be changed to accommodate the next number. This highlights the difficulty in finding a single simple rule for this sequence.
Scenario 2: A More Complex Recursive Rule
A more sophisticated approach might involve a recursive rule with multiple operations, such as adding a function of the previous number. This provides for more flexibility in fitting the known numbers.
For instance, we might explore rules like:
- f(x) = x + 5
- f(1) = 1 + 5 = 6 (Incorrect)
Again, modifying the approach to the sequence of numbers is necessary for the next element, illustrating that this isn't a direct match.
Scenario 3: A Rule Based on Position
We could also explore rules based on the position of each number in the sequence. For example:
- Position 1: x
- Position 2: f(1) = 1
- Position 3: f(2) = 6
- Position 4: f(3) = 2
- Position 5: f(4) = 3
This opens possibilities for functions of the position that map to the given sequence. The complexity of this function might be high, depending on how well it fits the sequence.
Conclusion: The Ongoing Search for Patterns
The sequence "x 1 6 2 3" serves as a compelling demonstration of the challenges and rewards of mathematical pattern recognition and problem-solving. While a definitive, universally agreed-upon solution may not exist without additional constraints or assumptions, exploring different approaches – arithmetic progressions, geometric progressions, polynomial functions, modular arithmetic, and logical/algorithmic rules – provides valuable insight into diverse mathematical concepts and techniques. The ambiguity inherent in the sequence highlights the importance of carefully considering the assumptions made and the creative approaches taken in tackling such problems. The process of investigation itself is as valuable as the potential solution, fostering critical thinking, analytical skills, and a deeper appreciation for the beauty and complexity of mathematics. The journey of exploring this seemingly simple sequence is a testament to the rich landscape of mathematical possibilities. Further investigation and experimentation with different approaches remain open, making this a puzzle that continues to invite exploration and debate.
FAQ
-
Q: Is there a single correct answer for 'x'? A: Without further constraints or context, there's no single definitively "correct" answer. Multiple solutions are likely depending on the assumed underlying rule.
-
Q: What mathematical concepts are relevant to solving this? A: Arithmetic progressions, geometric progressions, polynomial functions, modular arithmetic, recursion, and logical reasoning are all potentially applicable.
-
Q: Can this problem be solved using a computer program? A: Yes, a computer program could be used to explore different mathematical functions or algorithmic rules to search for patterns that fit the sequence.
-
Q: What if additional numbers were added to the sequence? A: Additional numbers would either confirm or refute potential rules, leading to a more refined understanding of the underlying pattern. More data generally increases the constraints on potential solutions.
-
Q: Why is this sequence considered a puzzle? A: Its seemingly simple presentation belies a lack of immediately obvious patterns. This challenge to find an underlying rule makes it a good exercise for problem-solving skills.
Latest Posts
Latest Posts
-
Gcf Of 50 And 30
Sep 11, 2025
-
4 5 8 As A Decimal
Sep 11, 2025
-
29 7 8 As A Decimal
Sep 11, 2025
-
8 Feet Divided By 3
Sep 11, 2025
-
Convert Lbs To Troy Oz
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X 1 6 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.