X 1 X 2 1
saludintensiva
Sep 23, 2025 · 7 min read
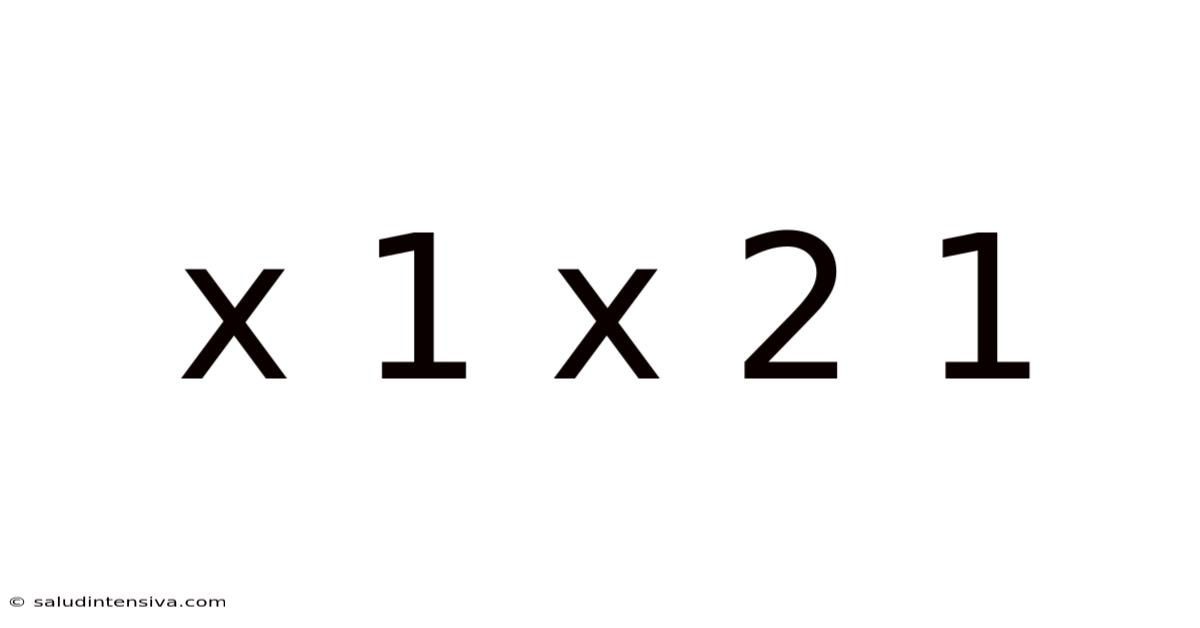
Table of Contents
Understanding the Sequence: x<sup>1</sup> x<sup>2</sup> 1 – A Deep Dive into Mathematical Patterns and Applications
This article explores the mathematical sequence represented by x<sup>1</sup> x<sup>2</sup> 1, delving into its underlying patterns, derivations, and diverse applications across various fields. We'll unpack its significance in algebra, calculus, and even beyond the realm of pure mathematics. This seemingly simple sequence holds a surprising depth, revealing connections between seemingly disparate areas of study. Understanding this sequence will provide a strong foundation for further exploration in mathematics and related disciplines.
Introduction: Decoding the Sequence
The sequence x<sup>1</sup> x<sup>2</sup> 1, often seen in simplified forms like x, x², 1, is more than just a collection of terms. It represents a fundamental building block in many mathematical concepts. At first glance, it might appear straightforward, but its implications are far-reaching, appearing in polynomial equations, quadratic formulas, and even within more complex mathematical structures. This article will dissect this sequence, examining its origins, properties, and the diverse ways it manifests itself in various mathematical contexts. We will explore its role in solving equations, understanding curves, and modeling real-world phenomena.
The Sequence in Polynomial Equations
One of the most immediate applications of this sequence is within the context of polynomial equations. Consider a simple quadratic equation: ax² + bx + c = 0. The sequence x, x², 1 corresponds directly to the powers of the variable x present in the equation. The coefficients a, b, and c are constants that determine the specific characteristics of the parabola represented by this equation. Understanding the relationship between the powers of x and the coefficients is crucial in solving quadratic equations, finding their roots (x-intercepts), and determining the vertex of the parabola. The sequence's presence provides a structured framework for analyzing and manipulating these equations.
For example, let’s analyze the equation 2x² + 5x + 3 = 0. We can clearly see the sequence x<sup>2</sup>, x<sup>1</sup>, and the constant term (x<sup>0</sup> = 1). This structure is fundamental in using methods like factoring, the quadratic formula, or completing the square to find the solutions for x.
Geometric Interpretation: Parabolas and Conic Sections
The sequence x, x², 1 also has a significant geometrical interpretation, most notably in relation to parabolas. A parabola is a conic section – a curve formed by the intersection of a cone and a plane. The equation of a parabola can often be expressed in the form y = ax² + bx + c, where the sequence x, x², 1 is clearly visible. This representation allows us to visualize the relationship between the variable x and the resulting y-coordinate, providing a geometric understanding of the quadratic equation. The shape, orientation, and position of the parabola are directly determined by the coefficients a, b, and c of the polynomial, highlighting the power of this seemingly simple sequence in visualising mathematical concepts. Furthermore, transformations applied to the parabola, such as translations, rotations, or scaling, can all be understood and calculated using manipulations of the coefficients within this structure.
Consider the parabola y = x². Here, we see the simplest form, where a = 1, b = 0, and c = 0. The sequence is directly reflected in the equation, providing a clear visual understanding of its underlying structure. As we change the values of a, b, and c, we modify the parabola's shape, position, and orientation, underscoring the sequence's crucial role in describing geometric transformations.
Calculus and the Sequence: Derivatives and Integrals
The sequence x, x², 1 plays a crucial role in calculus, particularly in differentiation and integration. The derivative of x<sup>n</sup> is nx<sup>n-1</sup>. This rule directly involves the power of x, demonstrating a direct connection to our sequence. For example, the derivative of x² is 2x, and the derivative of x is 1. The constant term (1) has a derivative of 0. This relationship underlines the inherent connection between the sequence and the fundamental operations of calculus.
Similarly, integration involves the reverse process. The indefinite integral of x<sup>n</sup> is (x<sup>n+1</sup>)/(n+1) + C, where C is the constant of integration. This integral rule directly manipulates the exponents, again showcasing the sequence's integral role in calculus. The consistent presence of this power-based sequence demonstrates its fundamental importance in understanding both differential and integral calculus. Many complex problems in physics and engineering utilize these calculus concepts, making the sequence a critical foundation.
Beyond Polynomials: Higher-Order Equations and Matrices
While the sequence's most straightforward application lies within quadratic equations, its significance extends to higher-order polynomials and even more abstract mathematical structures. In cubic equations (ax³ + bx² + cx + d = 0), the sequence x³, x², x, 1 appears, highlighting the generalizable nature of this pattern. This sequence continues to appear in polynomial equations of any degree, demonstrating its pervasiveness in algebraic manipulations.
Furthermore, the sequence's structure shows up in the context of matrices and linear algebra. Matrices, particularly those representing linear transformations, often contain elements arranged in patterns that reflect this underlying sequence. The concepts of eigenvalues and eigenvectors, crucial in linear algebra, often involve solving polynomial equations, further emphasizing the sequence’s indirect role in these areas. Understanding the sequence provides a foundational understanding that can be extended to more complex mathematical fields.
Applications in Physics and Engineering
The mathematical concepts built upon the x, x², 1 sequence find extensive application in various fields of physics and engineering. For example, projectile motion – the parabolic trajectory of an object under gravity – is directly modeled using quadratic equations, showcasing the practical applications of this sequence. Similarly, the design of bridges, parabolic antennas, and many other engineering structures uses parabolic shapes, requiring understanding of quadratic equations and therefore the sequence itself.
In physics, describing oscillations and wave phenomena often involves trigonometric functions which are related to exponentials, and therefore the sequence indirectly plays a role in modelling these systems as well. The sequence indirectly underpins some fundamental aspects of physics, illustrating its power beyond purely mathematical contexts.
The Sequence in Computer Science and Data Analysis
The sequence also holds relevance within computer science and data analysis. Polynomial interpolation, a crucial technique for approximating functions, heavily relies on polynomial equations and thus utilizes the x, x², 1 sequence. This technique is fundamental in many areas of computer graphics, numerical analysis, and machine learning. In data analysis, polynomial regression models use the sequence to estimate relationships between variables, enabling predictive analysis. Understanding polynomial equations and their inherent structure rooted in this sequence is therefore vital for working effectively in these fields.
Frequently Asked Questions (FAQ)
-
Q: Is the sequence always written in this order (x, x², 1)?
A: No, the order can be changed depending on the context. The important aspect is the presence of the terms x<sup>1</sup>, x<sup>2</sup>, and the constant term (x<sup>0</sup> = 1), regardless of their order.
-
Q: What happens if the coefficient of x² is zero?
A: If the coefficient of x² is zero, the equation becomes linear (ax + c = 0), and the quadratic behavior is lost. The sequence is still present, but the x² term is simply absent.
-
Q: Can this sequence be extended?
A: Yes, the sequence can be extended to include higher powers of x, like x³, x⁴, and so on, creating higher-order polynomial equations.
-
Q: Are there real-world examples of this sequence besides the ones mentioned?
A: Yes, numerous examples exist. Modeling the trajectory of a ball thrown in the air, calculating the area under a curve, and designing lenses are just some examples of this sequence's real-world application.
Conclusion: The Power of a Simple Sequence
The seemingly simple sequence x<sup>1</sup> x<sup>2</sup> 1 is a fundamental cornerstone in various areas of mathematics, science, and engineering. From solving quadratic equations and visualizing parabolas to performing calculus operations and modeling real-world phenomena, its influence is far-reaching and surprisingly profound. Understanding this sequence provides not just a grasp of its immediate applications but also lays a foundation for comprehending more advanced mathematical concepts and their applications across diverse fields. Its ubiquity emphasizes the interconnectedness of mathematical principles and their practical significance in a wide range of disciplines. While seemingly basic, this sequence represents a powerful tool for problem-solving and a gateway to understanding the elegant structures that underpin our world.
Latest Posts
Latest Posts
-
8 1 2 X 11
Sep 23, 2025
-
2 Million How Many Zeros
Sep 23, 2025
-
Is 62 A Rational Number
Sep 23, 2025
-
1 2 Psi To Wc
Sep 23, 2025
-
What Does Compounded Quarterly Mean
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 1 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.