X 2 3 9 10
saludintensiva
Sep 23, 2025 · 6 min read
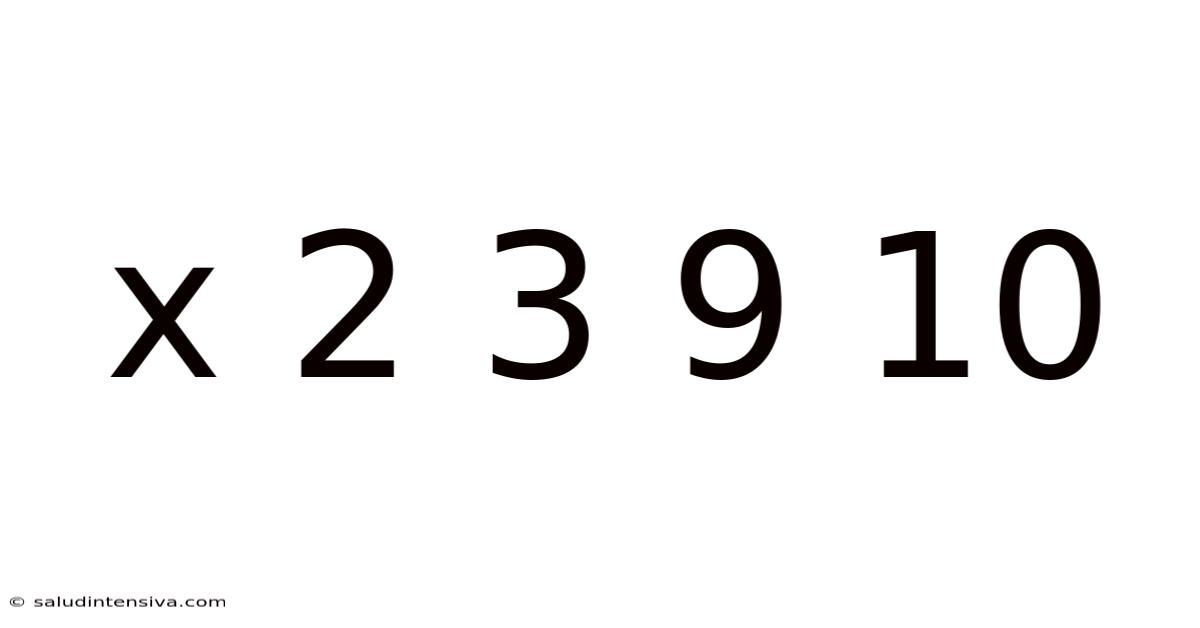
Table of Contents
Unlocking the Mystery: Exploring the Sequence X 2 3 9 10
This article delves into the intriguing mathematical sequence "X 2 3 9 10," exploring potential patterns, solutions, and the underlying mathematical concepts. We'll examine different approaches to solving this puzzle, considering various mathematical principles and offering a detailed explanation for each possibility. This will equip you with the tools to not only understand this specific sequence but also to approach similar number pattern problems with confidence. Understanding number sequences is a crucial skill in mathematics, critical for developing logical reasoning and problem-solving abilities.
Understanding the Problem: Defining the Variables
The core of the problem lies in determining the value of 'X'. The sequence provided – X, 2, 3, 9, 10 – presents a seemingly random arrangement of numbers. However, the challenge is to uncover the hidden logic or pattern connecting these numbers. This requires a systematic approach, exploring different mathematical operations and patterns to find a consistent relationship that accounts for all elements within the sequence. We will consider several possibilities, from simple arithmetic progressions to more complex patterns involving prime numbers or Fibonacci-like sequences.
Possible Solutions and Their Explanations
Several plausible solutions exist for this sequence, depending on the assumptions made about the underlying pattern. Let's explore some of the most likely possibilities:
1. A Non-Linear Sequence Based on Multiplication and Addition:
One possible approach is to identify a pattern involving both multiplication and addition. Let's examine the relationship between the known numbers:
- 2 to 3: An increase of 1 (2 + 1 = 3).
- 3 to 9: An increase of 6 (3 x 3 = 9).
- 9 to 10: An increase of 1 (9 + 1 = 10).
This sequence demonstrates a pattern that alternates between addition and multiplication. Observing this pattern, we might hypothesize a similar relationship between X and 2. For instance:
- If we add 1 to X, the result is 2. This would imply X = 1.
- Let's check if this works for the rest of the sequence:
- 1 + 1 = 2
- 2 x 3 = 6 (Doesn't fit the pattern)
This approach leads to an inconsistency, highlighting the need to explore alternative solutions.
2. A Composite Sequence with Separate Patterns:
This approach breaks down the problem into identifying smaller, self-contained patterns within the larger sequence. Let's analyze the sequence again:
- We might consider that the sequence is composed of two separate sub-sequences, one being odd and the other even.
- Considering the odd-positioned numbers (X, 3, 10) and even-positioned numbers (2, 9) might reveal a pattern within each sub-sequence, but it may not be apparent at this stage.
3. Utilizing Prime Numbers and Composites:
Another possibility involves the concept of prime and composite numbers.
- A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- A composite number is a positive integer that has at least one divisor other than 1 and itself.
Let's analyze the sequence through this lens:
- 2 is a prime number.
- 3 is a prime number.
- 9 is a composite number (3 x 3).
- 10 is a composite number (2 x 5).
There doesn't seem to be a clear pattern directly relating prime and composite numbers in this sequence. Therefore, it's unlikely that this approach will yield a simple solution.
4. Considering Geometric Progression with Variations:
Geometric progression involves a sequence where each term is the product of the previous term and a constant value (common ratio). While a strict geometric progression doesn't seem to apply here, we can explore variations:
- Let's assume X is 1.
- The sequence becomes: 1, 2, 3, 9, 10.
- The ratio between successive terms varies significantly: 2, 1.5, 3, 1.11... which makes a straightforward geometric progression improbable.
5. Exploring Recursive Relationships and Functions:
A recursive relationship defines a term in a sequence based on preceding terms. Similarly, a function could represent a relationship between the position of a term and its value. This requires more advanced mathematical tools. Finding a simple recursive formula might be possible, but it would require testing different function types and analyzing the results. This approach is more involved and requires a more in-depth mathematical understanding than basic arithmetic.
6. The Importance of Context and Additional Information:
It's crucial to acknowledge that without additional context or information, a definitive solution for 'X' might not exist. The given sequence alone might not constrain the solution to a single value. It might be part of a larger, more complex pattern not fully revealed by the provided data points.
Advanced Approaches and Mathematical Concepts
Let's briefly explore more sophisticated mathematical techniques that could be relevant in solving similar number pattern problems:
- Difference Tables: Constructing a table of differences between successive terms can reveal patterns in the rate of change.
- Polynomial Interpolation: If a pattern exhibits a polynomial relationship, polynomial interpolation can help determine the function governing the sequence.
- Generating Functions: Generating functions provide a powerful method to represent sequences analytically and uncover hidden relationships.
- Finite Difference Calculus: This area of mathematics provides tools for analyzing sequences and their derivatives.
Frequently Asked Questions (FAQ)
Q: Is there only one correct answer for X?
A: Without additional context or constraints, there's no guarantee of a single correct solution for X. Multiple solutions might satisfy different patterns or interpretations of the sequence.
Q: What mathematical concepts are essential to solving number pattern problems?
A: A strong foundation in arithmetic, algebra, and number theory is critical. Familiarity with sequences, series, prime numbers, and functions is highly beneficial.
Q: How can I improve my ability to solve these types of problems?
A: Practice is key. Work through various number pattern problems of increasing complexity. Develop a systematic approach, exploring different possibilities and testing your hypotheses.
Q: Are there online resources or tools available to help solve such sequences?
A: While specific tools dedicated solely to this might be limited, many mathematical software packages or online calculators can perform operations relevant to analyzing sequences, such as generating differences or performing polynomial regression.
Conclusion: Embracing the Ambiguity and the Journey
While a single, definitive answer for 'X' in the sequence X, 2, 3, 9, 10 might not be conclusively determined without additional information, the exploration itself has illuminated several valuable mathematical concepts and problem-solving strategies. The journey of attempting to solve this sequence highlights the importance of systematic analysis, creative thinking, and perseverance in the face of ambiguity. This process enhances analytical skills, cultivates a deeper understanding of mathematical principles, and instills a greater appreciation for the complexity and beauty inherent within seemingly simple number patterns. Remember, the process of exploring and analyzing, even without reaching a single definitive solution, is a crucial part of the learning experience. The key takeaway is not necessarily finding the one right answer, but developing a robust problem-solving mindset that can be applied across a wide range of mathematical challenges.
Latest Posts
Latest Posts
-
What Is 56 Divisible By
Sep 23, 2025
-
Whats An Acre In Feet
Sep 23, 2025
-
30x40 How Many Square Feet
Sep 23, 2025
-
Gpa Converter 100 To 4
Sep 23, 2025
-
Australian 20 Cent Coin Value
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 3 9 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.