X 2 8x 12 Factor
saludintensiva
Sep 21, 2025 · 5 min read
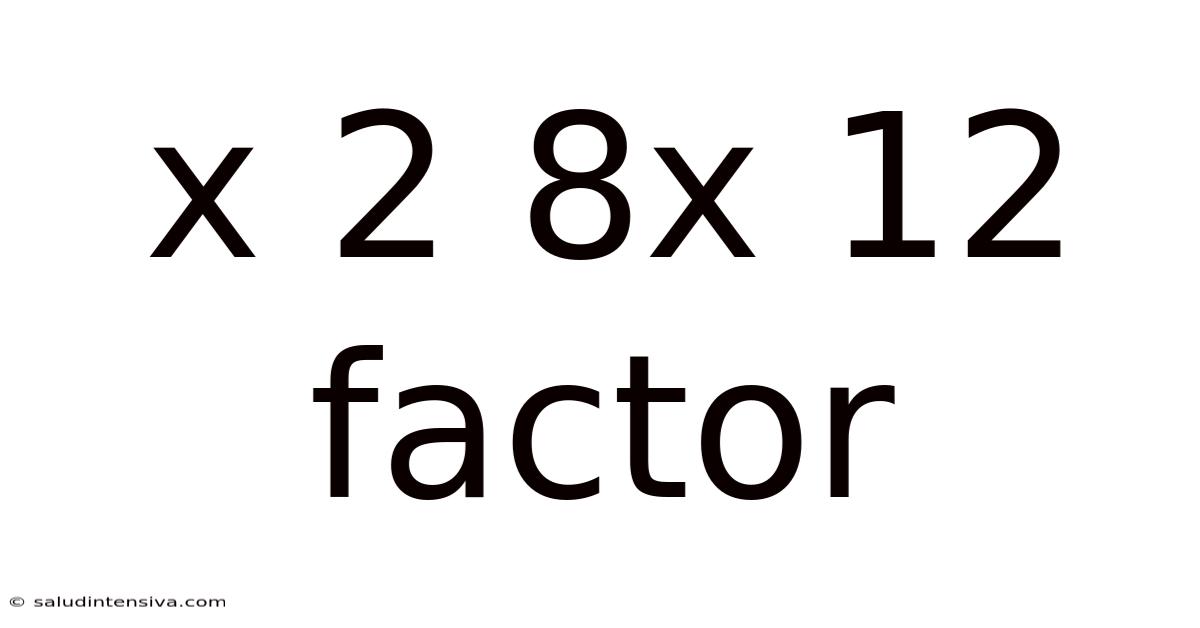
Table of Contents
Decoding the X^2 + 8X + 12 Factor: A Comprehensive Guide
Understanding quadratic equations is fundamental to success in algebra and beyond. This article delves deep into the factorization of the quadratic expression x² + 8x + 12, explaining the process step-by-step, exploring the underlying mathematical principles, and offering practical applications. We'll cover various methods, address common difficulties, and equip you with the tools to confidently tackle similar problems. By the end, you'll not only be able to factor this specific expression but also understand the broader concepts involved in factoring quadratic equations.
Introduction: What is Factoring?
Factoring, in the context of algebra, is the process of breaking down a mathematical expression into simpler expressions that, when multiplied together, yield the original expression. For example, factoring the number 12 might give you 3 x 4 or 2 x 6. Similarly, factoring a quadratic expression like x² + 8x + 12 involves finding two binomial expressions (expressions with two terms) whose product equals the original quadratic. This skill is crucial for solving quadratic equations, simplifying complex expressions, and understanding a wide range of mathematical concepts.
Method 1: The Traditional Factoring Method
This method involves finding two numbers that satisfy two specific conditions:
- Their sum equals the coefficient of the x term (8 in this case).
- Their product equals the constant term (12 in this case).
Let's apply this to x² + 8x + 12:
We need to find two numbers that add up to 8 and multiply to 12. Let's consider the factors of 12:
- 1 x 12
- 2 x 6
- 3 x 4
Analyzing these pairs:
- 1 + 12 = 13 (Incorrect)
- 2 + 6 = 8 (Correct!)
- 3 + 4 = 7 (Incorrect)
We've found our pair: 2 and 6. Therefore, we can factor x² + 8x + 12 as:
(x + 2)(x + 6)
To verify, let's expand this factored form using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * 6 = 6x
- Inner: 2 * x = 2x
- Last: 2 * 6 = 12
Combining these terms, we get x² + 6x + 2x + 12 = x² + 8x + 12, confirming our factorization.
Method 2: The AC Method (for more complex quadratics)
While the traditional method works well for simpler quadratics, the AC method is more robust and applicable to more complex expressions. This method is particularly useful when the coefficient of the x² term is not 1. While not strictly necessary for x² + 8x + 12, it's valuable to understand for future problems.
The AC method involves these steps:
-
Identify a, b, and c: In the general quadratic equation ax² + bx + c, identify the coefficients a, b, and c. In our case, a = 1, b = 8, and c = 12.
-
Find the product ac: ac = 1 * 12 = 12.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 8 and multiply to 12. As we've already established, these numbers are 2 and 6.
-
Rewrite the middle term: Rewrite the middle term (8x) as the sum of the two numbers we found, multiplied by x: 2x + 6x. Our expression becomes x² + 2x + 6x + 12.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x²(x + 2) + 6(x + 2)
-
Factor out the common binomial: Notice that (x + 2) is common to both terms. Factor it out:
(x + 2)(x + 6)
This yields the same result as the traditional method.
Understanding the Underlying Mathematics
The ability to factor x² + 8x + 12 relies on understanding the distributive property of multiplication. The distributive property states that a(b + c) = ab + ac. Factoring is essentially the reverse of this process. We are breaking down a sum of terms (x² + 8x + 12) into a product of simpler expressions ((x + 2)(x + 6)). This relationship is fundamental to many algebraic manipulations.
The specific numbers we choose (2 and 6) are crucial because they represent the roots of the quadratic equation x² + 8x + 12 = 0. When we set (x + 2)(x + 6) = 0, we find that x = -2 or x = -6. These values, when substituted into the original equation, will make the equation true.
Solving Quadratic Equations Using Factoring
Factoring a quadratic expression is a critical step in solving quadratic equations. Once you've factored the expression, you can use the zero product property, which states that if the product of two factors is zero, then at least one of the factors must be zero.
For example, to solve x² + 8x + 12 = 0:
- Factor the quadratic: (x + 2)(x + 6) = 0
- Apply the zero product property: Either (x + 2) = 0 or (x + 6) = 0
- Solve for x: x = -2 or x = -6
These are the solutions (or roots) to the quadratic equation.
Applications of Factoring
Factoring quadratic expressions has numerous applications across various fields, including:
- Physics: Solving problems involving projectile motion or calculating the trajectory of objects.
- Engineering: Designing structures, optimizing systems, and modeling various phenomena.
- Economics: Analyzing market trends, forecasting economic growth, and creating mathematical models for financial situations.
- Computer Science: Developing algorithms, solving optimization problems, and creating computer graphics.
Frequently Asked Questions (FAQ)
- What if the quadratic expression cannot be factored? Not all quadratic expressions can be factored using integer coefficients. In such cases, you can use the quadratic formula to find the roots.
- Are there other methods for factoring quadratics? Yes, the quadratic formula and completing the square are alternative methods for solving quadratic equations, which are particularly useful when factoring is not straightforward.
- How can I improve my factoring skills? Practice is key! Work through numerous examples, starting with simpler expressions and gradually increasing the complexity.
Conclusion: Mastering Quadratic Factoring
Mastering the art of factoring quadratic expressions, such as x² + 8x + 12, is a cornerstone of algebraic proficiency. Understanding the underlying principles, exploring different methods, and practicing regularly will build your confidence and equip you with a powerful tool for solving a wide array of mathematical problems. This skill is not just about manipulating symbols; it's about understanding the fundamental relationships between numbers and expressions, which are applicable across numerous fields of study and real-world applications. Remember that consistent practice and a methodical approach are the keys to unlocking your full potential in algebra and beyond. Don't be afraid to tackle challenging problems; each one solved brings you closer to mastery.
Latest Posts
Latest Posts
-
Cube Root And Square Root
Sep 21, 2025
-
What Is 2 3 Plus 1 4
Sep 21, 2025
-
6 Grados Fahrenheit A Centigrados
Sep 21, 2025
-
Day Of Week Google Sheets
Sep 21, 2025
-
1 Atm To Inches Hg
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 2 8x 12 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.