X 3 5x 2 6x
saludintensiva
Sep 23, 2025 · 6 min read
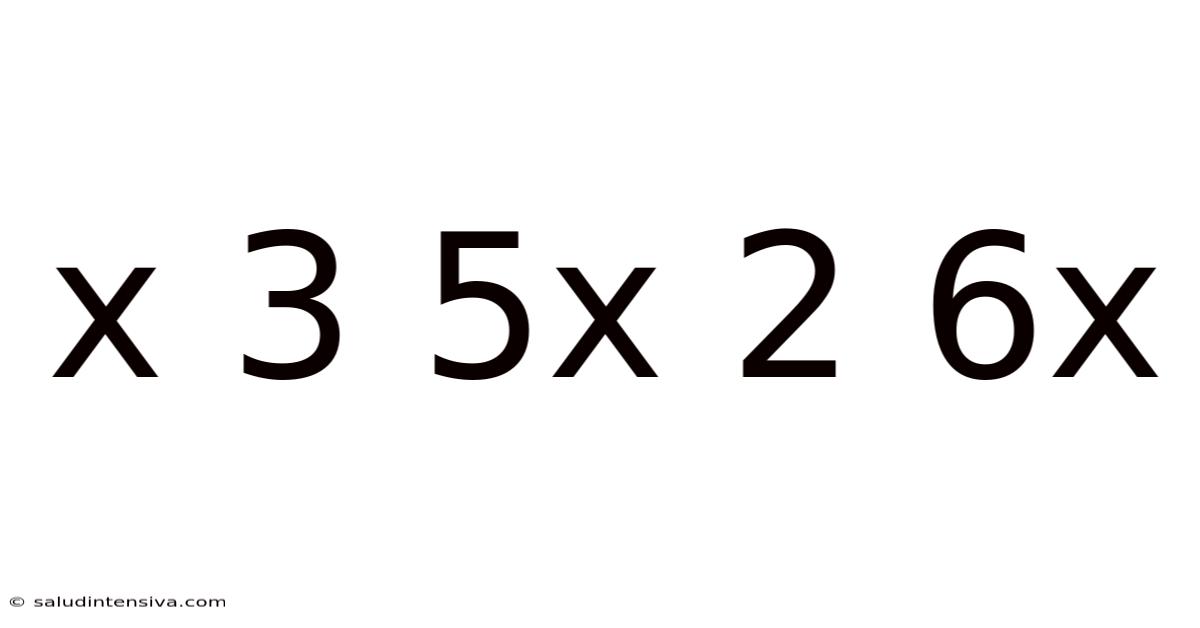
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression x³ + 5x² + 6x
This article delves into the mathematical expression x³ + 5x² + 6x, exploring its properties, methods for solving it, and its practical applications. We'll unpack this seemingly simple expression, revealing its underlying complexities and showing how it can be manipulated and understood. This exploration will cover factoring, finding roots, graphing the function, and discussing real-world scenarios where such expressions appear. Understanding cubic equations like this one is fundamental to many areas of mathematics and science.
Introduction: Understanding Cubic Polynomials
The expression x³ + 5x² + 6x is a cubic polynomial. A polynomial is an expression consisting of variables (in this case, 'x') and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. "Cubic" refers to the highest power of the variable, which is 3 (x³). Understanding cubic polynomials is crucial in various fields, from physics and engineering to economics and computer science. They represent a wide range of phenomena, and their solutions provide valuable insights into complex systems. This article will equip you with the knowledge and tools to confidently tackle such expressions.
Factoring the Cubic Polynomial: The Key to Understanding
The first step in understanding x³ + 5x² + 6x is to factor it. Factoring involves breaking down the expression into simpler components that, when multiplied together, give the original expression. This process is fundamental to solving the equation x³ + 5x² + 6x = 0 and to analyzing the function y = x³ + 5x² + 6x.
The most straightforward approach is to look for a common factor among all the terms. Notice that each term (x³, 5x², and 6x) contains an 'x'. We can factor out this 'x':
x³ + 5x² + 6x = x(x² + 5x + 6)
Now we have a simpler quadratic expression within the parentheses: x² + 5x + 6. This can be factored further. We are looking for two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term). These numbers are 2 and 3. Therefore, the quadratic can be factored as:
x² + 5x + 6 = (x + 2)(x + 3)
Putting it all together, the completely factored form of the original cubic polynomial is:
x³ + 5x² + 6x = x(x + 2)(x + 3)
This factored form is invaluable because it reveals the roots of the equation and provides insight into the function's behavior.
Finding the Roots: Solving the Equation x³ + 5x² + 6x = 0
The roots, or zeros, of a polynomial are the values of x that make the polynomial equal to zero. Finding the roots is crucial for understanding the behavior of the polynomial. Since we've factored the cubic polynomial, finding the roots is straightforward. We set the factored expression equal to zero:
x(x + 2)(x + 3) = 0
This equation is true if any of the factors are equal to zero. This gives us three roots:
- x = 0
- x + 2 = 0 => x = -2
- x + 3 = 0 => x = -3
Therefore, the roots of the equation x³ + 5x² + 6x = 0 are 0, -2, and -3. These roots represent the x-intercepts of the graph of the function y = x³ + 5x² + 6x.
Graphing the Cubic Function: Visualizing the Polynomial
Graphing the function y = x³ + 5x² + 6x provides a visual representation of the polynomial's behavior. Knowing the roots (0, -2, -3) is crucial for sketching the graph. The graph will intersect the x-axis at these points.
The graph of a cubic function typically has two turning points (local maximum and minimum). To find these points, we could use calculus (taking the derivative and setting it to zero), but a simpler approach is to analyze the factored form and the behavior of the function between the roots. The graph will pass through (0,0) and will show that the function increases from negative infinity, then decreases, then increases again to positive infinity.
Further Analysis: Exploring the Behavior of the Function
The factored form, x(x + 2)(x + 3), also helps us understand the function's behavior. For instance:
- When x < -3: All three factors are negative, resulting in a negative value for y.
- When -3 < x < -2: (x+3) is positive, while x and (x+2) are negative. This results in a positive value for y.
- When -2 < x < 0: (x+3) and (x+2) are positive, while x is negative. This results in a negative value for y.
- When x > 0: All three factors are positive, resulting in a positive value for y.
This analysis confirms the general shape of the cubic graph, showing the changes in sign around the roots. You can use this information to sketch a reasonably accurate graph without needing sophisticated graphing tools. Remember to label the x-intercepts (the roots) and the y-intercept (found by setting x=0, which gives y=0 in this case).
Applications of Cubic Polynomials: Real-World Relevance
Cubic polynomials are not just abstract mathematical objects; they have numerous practical applications:
- Physics: They are used to model the motion of projectiles under the influence of gravity, where the height is a function of time. The roots could represent the times when the projectile is at ground level.
- Engineering: Cubic functions are used in structural analysis, determining the stress and strain in beams and other structures.
- Economics: They can model cost functions or production functions, helping businesses to optimize their operations.
- Computer graphics: Cubic curves (Bézier curves) are fundamental to creating smooth curves and shapes in computer-aided design and other graphical applications.
- Data analysis: Cubic regression is a technique used to fit a cubic polynomial to a set of data points, allowing for the approximation and prediction of trends.
Frequently Asked Questions (FAQ)
Q: Can all cubic polynomials be factored easily?
A: No. While some cubic polynomials, like this one, factor easily, others may require more sophisticated techniques like the cubic formula or numerical methods to find their roots. Some cubic polynomials might not even have real roots; they might have complex roots.
Q: What if the coefficient of x³ is not 1?
A: If the coefficient of x³ is not 1, factoring can become more challenging. Techniques like grouping or rational root theorem may be necessary to find the factors.
Q: Are there other ways to find the roots of a cubic polynomial besides factoring?
A: Yes. The cubic formula, analogous to the quadratic formula, can be used to find the roots, but it's significantly more complex than the quadratic formula. Numerical methods, such as Newton-Raphson, are often used to approximate the roots, especially when the cubic formula is impractical.
Conclusion: Mastering Cubic Polynomials
This in-depth exploration of the cubic polynomial x³ + 5x² + 6x has shown how factoring, finding roots, and graphing can provide a comprehensive understanding of its behavior. We’ve moved from a seemingly simple algebraic expression to a deeper comprehension of its properties and practical applications. Mastering cubic polynomials, and polynomials in general, is a cornerstone of mathematical literacy and has far-reaching implications across numerous disciplines. The techniques discussed here are applicable to a wide range of similar problems and provide a solid foundation for tackling more complex mathematical challenges. Remember that practice is key – the more you work with these concepts, the more intuitive and effortless they will become.
Latest Posts
Latest Posts
-
How To Balance A Checkbook
Sep 23, 2025
-
Whats 30 Percent Of 750
Sep 23, 2025
-
Convert 230 Celsius To Fahrenheit
Sep 23, 2025
-
Percent Of Increase Word Problems
Sep 23, 2025
-
Convert Decimal To Inch Fractions
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 3 5x 2 6x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.