X 4 X 5 2
saludintensiva
Sep 17, 2025 · 5 min read
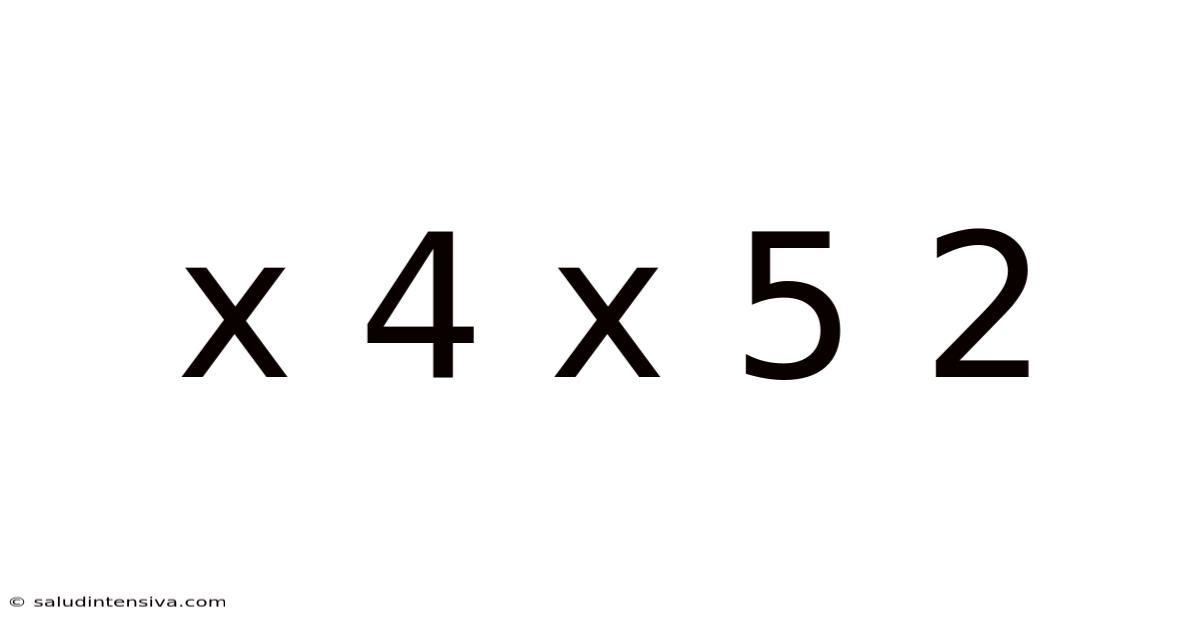
Table of Contents
Decoding the Enigma: A Deep Dive into x4x5²
The seemingly simple expression "x⁴x⁵²" presents a fascinating challenge, blending basic algebraic concepts with opportunities for deeper mathematical exploration. This article will dissect this expression, examining its components, clarifying potential ambiguities, and exploring various interpretations and solutions. We will cover the order of operations, the rules of exponents, and even delve into the potential for more complex interpretations if we consider 'x' as a matrix or operator. Understanding this seemingly simple equation requires a solid grasp of fundamental mathematical principles, and this article aims to provide that, leaving you with a clearer and more comprehensive understanding.
Understanding the Components: Variables and Exponents
At its core, "x⁴x⁵²" involves only one variable, 'x', and several exponents. Let's break down each part:
-
x: This represents an unknown value or variable. It can represent any real number, complex number, or even a matrix, depending on the context. Without further information, we assume 'x' represents a real number.
-
⁴: This is an exponent, indicating that 'x' is multiplied by itself four times (x⁴ = x * x * x * x).
-
⁵²: This is another exponent, representing 'x' raised to the power of 52 (x⁵² = x * x * x * ... * x (52 times)).
Order of Operations (PEMDAS/BODMAS): The Key to Clarity
Before proceeding, it's crucial to address the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics highlight the sequence in which mathematical operations must be performed to obtain the correct result. In our case, there are no parentheses or brackets. Therefore, we focus on exponents and multiplication.
In our expression "x⁴x⁵²", the exponents are applied before the multiplication. We don't have explicit multiplication symbols between x⁴ and x⁵², but implied multiplication exists between terms in algebra. This means we first calculate x⁴ and x⁵², and then multiply the results.
Calculating x⁴ and x⁵²: Applying the Rules of Exponents
The rules of exponents are essential for simplifying this expression. The most relevant rule here is the product of powers rule: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾. This rule states that when multiplying terms with the same base (in this case, 'x'), you can add their exponents.
Therefore:
x⁴x⁵² = x⁽⁴⁺⁵²⁾ = x⁵⁶
This simplification significantly reduces the complexity of the original expression. The final result, regardless of the value of 'x', is simply x raised to the power of 56.
Illustrative Examples with Numerical Values
To further clarify, let's substitute numerical values for 'x' to see the outcome:
-
If x = 2: 2⁴ * 2⁵² = 2⁵⁶ ≈ 7.2 x 10¹⁶ (a very large number!)
-
If x = 3: 3⁴ * 3⁵² = 3⁵⁶ ≈ 1.2 x 10²⁷ (an even larger number!)
-
If x = 1: 1⁴ * 1⁵² = 1⁵⁶ = 1 (any number raised to the power of zero is 1)
-
If x = 0: 0⁴ * 0⁵² = 0 (zero raised to any positive power is zero)
-
If x = -1: (-1)⁴ * (-1)⁵² = (-1)⁵⁶ = 1 (any negative number raised to an even power is positive)
These examples demonstrate that the final result is always a power of the base 'x', regardless of the initial value. The magnitude of the result, however, drastically increases as the base 'x' and the resulting exponent increase.
Exploring More Complex Interpretations: Matrices and Operators
While our primary interpretation involves real numbers, let's briefly consider alternative scenarios:
-
Matrices: If 'x' represents a square matrix, then x⁴ and x⁵² would involve matrix multiplication. The result (x⁵⁶) would be another matrix, subject to the rules of matrix multiplication. The process would be significantly more complex and would depend entirely on the dimensions and entries of matrix 'x'.
-
Operators: In advanced mathematical fields like functional analysis, 'x' could symbolize an operator. In this context, x⁴x⁵² would involve composing operators, a procedure with its own set of rules and implications depending on the nature of the operator 'x'. This requires a deep understanding of abstract algebra and functional analysis.
Addressing Potential Ambiguities and Misinterpretations
One might initially misinterpret the expression as (x⁴)⁵², which is not the case. Remember, we apply exponents before multiplication. If the intention was to raise x⁴ to the power of 52, the expression should have been written as (x⁴)⁵² which, according to the power of a power rule, would simplify to x²⁰⁸. This highlights the importance of correct notation in mathematical expressions.
Frequently Asked Questions (FAQs)
Q: What if there were parentheses in the expression?
A: The presence of parentheses would dramatically alter the order of operations. For example, (x⁴x⁵)² would imply that the product of x⁴ and x⁵ is squared, resulting in x¹⁸. The placement of parentheses dictates the sequence of operations.
Q: Can this expression be further simplified?
A: In its simplest form for real numbers, x⁴x⁵² simplifies to x⁵⁶. There is no further simplification unless we know a numerical value for 'x'.
Q: What is the significance of this expression?
A: While this specific expression might not have immediate practical applications outside a mathematical context, it serves as an excellent exercise in understanding fundamental algebraic concepts: order of operations, exponent rules, and the importance of notation. It also opens the door to more abstract mathematical concepts like matrix algebra and operator theory.
Conclusion: A Journey Through Fundamental Concepts
The seemingly simple expression "x⁴x⁵²" offers a comprehensive overview of fundamental mathematical principles. From the order of operations and exponent rules to the potential for more complex interpretations involving matrices or operators, we've explored various aspects of this problem. By breaking it down step by step, we've shown how a seemingly simple equation can be used to reinforce our understanding of core mathematical concepts. The journey from a seemingly simple expression to a deeper understanding of mathematical principles highlights the power and beauty of mathematics itself. Mastering these concepts provides a strong foundation for tackling more advanced mathematical challenges.
Latest Posts
Latest Posts
-
What Are Multiples Of 100
Sep 17, 2025
-
37 20 As A Decimal
Sep 17, 2025
-
200 Percent In Decimal Form
Sep 17, 2025
-
17 3 As A Mixed Number
Sep 17, 2025
-
1 2 5 As A Percent
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.