1 000 Divided By 3
saludintensiva
Sep 13, 2025 · 6 min read
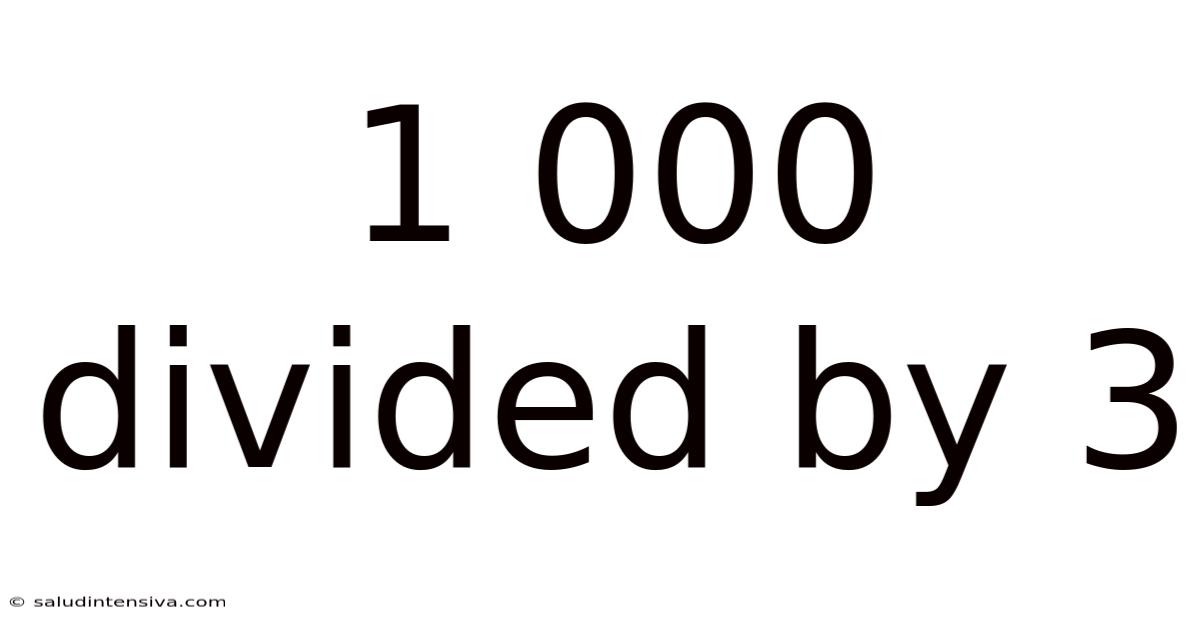
Table of Contents
Unveiling the Mystery: 1000 Divided by 3 and the Wonders of Division
Dividing 1000 by 3 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation opens a door to a deeper understanding of division, fractions, decimals, and even the fascinating world of remainders. This article will explore this seemingly simple problem in detail, delving into the process, the resulting answer, and the broader mathematical concepts it illuminates. We'll cover various methods of solving this problem, explain the meaning of the result, and explore its implications in different contexts. By the end, you'll not only know the answer to 1000 divided by 3 but also possess a more robust understanding of fundamental mathematical principles.
Understanding Division: A Foundation
Before diving into the specifics of 1000 divided by 3, let's establish a solid understanding of the concept of division itself. Division is essentially the process of splitting a whole into equal parts. In the expression "a ÷ b," 'a' represents the dividend (the number being divided), 'b' represents the divisor (the number you're dividing by), and the result is called the quotient. Sometimes, division results in a whole number, but often, we encounter remainders.
A remainder is the amount left over after dividing a number as evenly as possible. For instance, if you divide 7 by 2, you get a quotient of 3 with a remainder of 1 (because 2 x 3 = 6, and 7 - 6 = 1). Understanding remainders is crucial when dealing with divisions that don't result in a whole number.
Methods for Solving 1000 ÷ 3
There are several ways to calculate 1000 divided by 3:
1. Long Division: This is a classic method taught in schools. It involves a step-by-step process of dividing the dividend (1000) by the divisor (3).
333
3 | 1000
-9
10
-9
10
-9
1
This shows that 1000 divided by 3 is 333 with a remainder of 1.
2. Repeated Subtraction: This method involves repeatedly subtracting the divisor (3) from the dividend (1000) until you reach a number less than the divisor. The number of times you subtract represents the quotient, and the remaining number is the remainder. While less efficient for larger numbers, it illustrates the core concept of division.
3. Using a Calculator: The simplest and often quickest method is to use a calculator. Simply enter "1000 ÷ 3" and the calculator will return the result: 333.3333... This decimal representation shows that the division doesn't result in a whole number.
Decimals and Fractions: Interpreting the Result
The calculator's result, 333.3333..., highlights the importance of understanding decimals and fractions. The repeating decimal 0.333... represents one-third (1/3). Therefore, 1000 ÷ 3 can be expressed as 333 and 1/3. This mixed number combines a whole number (333) with a fraction (1/3) to represent the complete result.
The Significance of the Remainder
The remainder of 1 in 1000 ÷ 3 is crucial. It signifies that 1000 cannot be perfectly divided into groups of 3. There will always be one item left over. This remainder is essential in various applications, such as determining how many groups of 3 can be formed from 1000 items, or how to distribute 1000 objects evenly among 3 people.
Real-World Applications: Where does this calculation matter?
Understanding 1000 ÷ 3 isn't just an academic exercise; it has practical applications across numerous fields:
-
Resource Allocation: Imagine distributing 1000 candies equally among 3 children. Each child would receive 333 candies, with one candy remaining. This extra candy would need separate consideration.
-
Inventory Management: If you have 1000 items in stock and need to package them into groups of 3, you can create 333 packages with one item leftover. This leftover item needs to be accounted for in your inventory system.
-
Construction and Engineering: Many construction projects involve precise measurements and calculations. Understanding remainders is vital for accurate cutting of materials or distribution of resources. For instance, dividing 1000 meters of wire into 3-meter sections would leave one meter of wire.
-
Data Analysis: In statistical analysis, dealing with remainders helps interpret data and understand patterns that wouldn’t be apparent by simply rounding.
-
Computer Science: In computer programming, the remainder operation (often represented as the modulo operator, %) is widely used for tasks like determining if a number is even or odd, generating patterns, and managing data structures.
Exploring Further: Expanding the Concept
The seemingly simple problem of 1000 ÷ 3 provides a springboard for exploring more advanced mathematical concepts:
-
Modular Arithmetic: The remainder of a division is central to modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). The remainder when 1000 is divided by 3 (which is 1) is the result in modulo 3 arithmetic.
-
Fractional Representation: Representing the result as 333 1/3 allows for a more accurate representation than the truncated decimal 333.33. Fractions are essential for precise calculations, especially in scientific and engineering applications.
-
Infinite Decimals: The repeating decimal 333.333... is an example of an infinite decimal, which highlights the concept of limits and infinite series in calculus.
-
Approximations: Depending on the application, rounding the result to the nearest whole number (333) might be acceptable, but this introduces a degree of error that should be considered. Understanding this error margin is crucial in many applications.
Frequently Asked Questions (FAQ)
Q: What is the exact answer to 1000 divided by 3?
A: The exact answer is 333 with a remainder of 1, or expressed as a mixed number: 333 1/3. As a decimal, it's 333.333... (a repeating decimal).
Q: Why is there a remainder?
A: There is a remainder because 1000 is not evenly divisible by 3. 3 does not divide into 1000 without leaving a remainder.
Q: How can I use this information in real-life scenarios?
A: The knowledge of division, remainders, and the resulting fraction can be used in resource allocation, inventory management, construction, data analysis, and many other fields where precise distribution or grouping is necessary.
Q: What are the different ways to represent the answer?
A: The answer can be represented as a whole number with a remainder (333 R1), a mixed number (333 1/3), a repeating decimal (333.333...), or simply as an approximation (333).
Conclusion: Beyond the Numbers
This exploration of 1000 divided by 3 demonstrates that even seemingly basic arithmetic problems can lead to a deeper understanding of mathematical principles. By examining the process, the result, and its implications, we've highlighted the importance of understanding division, remainders, decimals, fractions, and their applications in various real-world scenarios. Remember that the seemingly simple act of division reveals a rich tapestry of mathematical concepts that are essential for problem-solving and critical thinking across disciplines. Next time you encounter a division problem, take a moment to appreciate the underlying principles at play—you might be surprised at what you discover.
Latest Posts
Latest Posts
-
Gcf Of 40 And 28
Sep 13, 2025
-
13 Out Of 20 Percent
Sep 13, 2025
-
14 Percent As A Fraction
Sep 13, 2025
-
What Percent Is 1 16
Sep 13, 2025
-
16000 Sq Ft To Acres
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 000 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.