13 Out Of 20 Percent
saludintensiva
Sep 13, 2025 · 6 min read
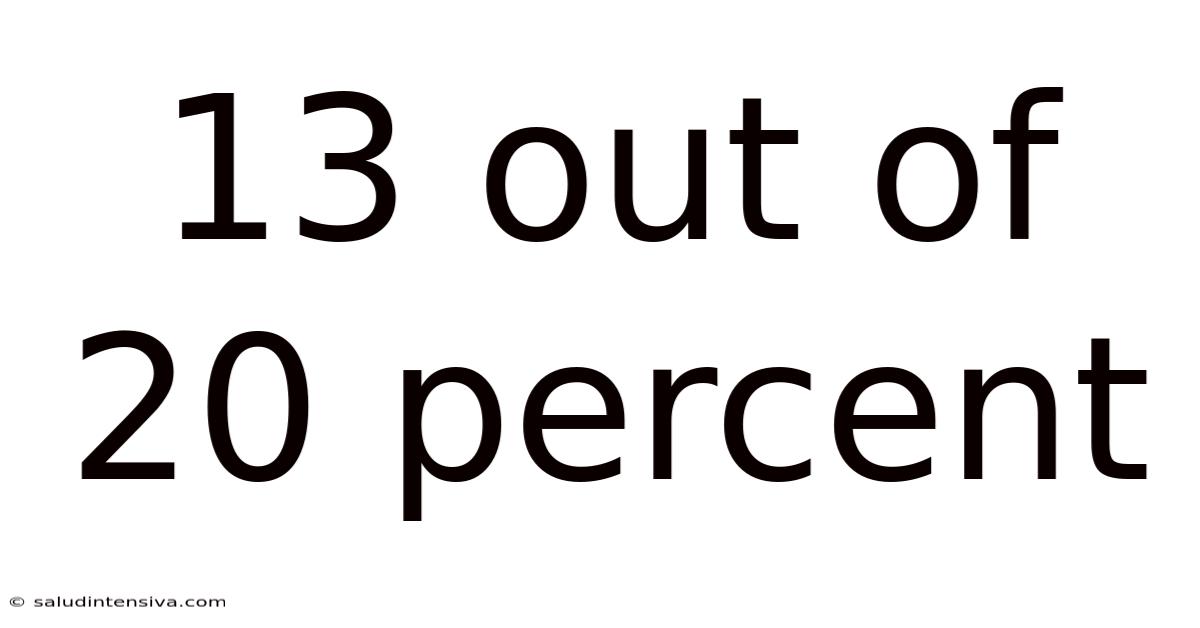
Table of Contents
Understanding 13 out of 20: A Comprehensive Guide to Percentages and Fractions
Understanding percentages and fractions is a fundamental skill applicable in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the concept of "13 out of 20," explaining its representation as a fraction, decimal, and percentage, along with practical examples and applications. We will explore the underlying mathematical principles and provide a clear, step-by-step guide to help you confidently tackle similar percentage problems. This comprehensive guide will equip you with the knowledge to solve percentage problems efficiently and accurately.
Introduction: Deconstructing "13 out of 20"
The phrase "13 out of 20" signifies a part-to-whole relationship. It means that out of a total of 20 items or units, 13 possess a specific characteristic or attribute. This simple phrase forms the basis for understanding various mathematical concepts. We will explore how to express this relationship as a fraction, decimal, and percentage.
1. Representing "13 out of 20" as a Fraction
A fraction represents a part of a whole. In this case, 13 is the part and 20 is the whole. Therefore, "13 out of 20" is represented as the fraction 13/20. This fraction is already in its simplest form because 13 is a prime number and does not share any common factors with 20 other than 1. This means we cannot simplify the fraction further by dividing both the numerator (13) and the denominator (20) by a common number.
2. Converting the Fraction to a Decimal
To convert the fraction 13/20 into a decimal, we simply divide the numerator (13) by the denominator (20):
13 ÷ 20 = 0.65
Therefore, 13 out of 20 is equivalent to 0.65.
3. Converting the Fraction/Decimal to a Percentage
A percentage represents a fraction or decimal expressed as a part of 100. To convert the decimal 0.65 to a percentage, we multiply it by 100 and add the "%" symbol:
0.65 × 100 = 65%
Therefore, 13 out of 20 is equivalent to 65%. This means that 13 represents 65% of the total 20.
4. Understanding the Mathematical Principles Involved
The conversion from fraction to decimal and then to percentage involves fundamental mathematical principles:
- Division: Converting a fraction to a decimal involves dividing the numerator by the denominator.
- Multiplication: Converting a decimal to a percentage involves multiplying the decimal by 100.
- Proportionality: Percentages express proportionality. 65% means 65 parts per 100 parts, which is equivalent to 13 parts per 20 parts.
5. Real-World Applications of 13 out of 20 (65%)
The concept of 13 out of 20, or 65%, appears frequently in various real-world scenarios:
- Test Scores: If a student answers 13 questions correctly out of 20 on a test, their score is 65%.
- Sales and Discounts: A store might offer a 65% discount on certain items.
- Surveys and Polls: 65% of respondents might agree with a particular opinion in a survey.
- Statistics and Data Analysis: In statistical analysis, percentages are used extensively to represent proportions and trends within datasets. For example, a study might reveal that 65% of a particular population exhibits a certain characteristic.
- Financial Calculations: Interest rates, tax calculations, and investment returns are often expressed as percentages.
- Probability: The probability of an event occurring can be expressed as a percentage. For example, there's a 65% chance of rain.
6. Solving Related Percentage Problems
Let's explore some related percentage problems to reinforce our understanding:
Example 1: If a class has 20 students, and 13 of them passed a test, what percentage of students passed?
- Solution: This is directly analogous to our initial problem. 13 out of 20 is 65%. Therefore, 65% of the students passed the test.
Example 2: A store offers a 65% discount on a $100 item. What is the discount amount?
- Solution: To find the discount amount, multiply the original price by the discount percentage (expressed as a decimal): $100 × 0.65 = $65. The discount amount is $65.
Example 3: A survey showed that 65% of 500 people prefer Brand A. How many people prefer Brand A?
- Solution: To find the number of people who prefer Brand A, multiply the total number of people by the percentage (expressed as a decimal): 500 × 0.65 = 325. 325 people prefer Brand A.
Example 4: If 13 out of 20 apples are ripe, what fraction of the apples are unripe?
- Solution: If 13 apples are ripe, then 20 - 13 = 7 apples are unripe. The fraction of unripe apples is 7/20.
7. Advanced Concepts and Extensions
Understanding 13 out of 20 lays the groundwork for more advanced concepts:
- Ratios: The concept of "13 out of 20" can also be expressed as a ratio: 13:20 or 13/20. Ratios compare the relative sizes of two or more values.
- Proportions: Proportions are equations stating that two ratios are equal. For example, 13/20 = x/100 can be solved to find the percentage (x=65).
- Statistical Inference: In statistics, percentages are used to make inferences about populations based on samples. For example, if 65% of a sample prefers a certain product, we might infer that a similar percentage of the entire population prefers the same product.
8. Frequently Asked Questions (FAQs)
-
Q: How do I calculate a percentage of a number?
- A: To calculate a percentage of a number, convert the percentage to a decimal (by dividing by 100) and then multiply the decimal by the number. For example, 25% of 80 is 0.25 × 80 = 20.
-
Q: What is the difference between a fraction, a decimal, and a percentage?
- A: They all represent parts of a whole, but in different forms. A fraction expresses the part as a ratio (numerator/denominator), a decimal expresses it as a base-10 number, and a percentage expresses it as a part of 100.
-
Q: Can I express 13 out of 20 as a different percentage?
- A: No, 13 out of 20 will always be equivalent to 65%. The percentage is a fixed representation of the ratio.
-
Q: How do I convert a percentage back to a fraction?
- A: Divide the percentage by 100 and simplify the resulting fraction. For example, 65% becomes 65/100, which simplifies to 13/20.
-
Q: Are there any online tools or calculators to help with percentage calculations?
- A: Yes, many online calculators are available to perform percentage calculations quickly and accurately. However, understanding the underlying principles is crucial for problem-solving beyond simple calculations.
9. Conclusion: Mastering Percentages and Fractions
Understanding the concept of "13 out of 20" provides a solid foundation for mastering percentages and fractions. By grasping the principles of conversion between fractions, decimals, and percentages, you will be equipped to handle a wide range of mathematical problems in various contexts. This skill is invaluable not only for academic success but also for navigating everyday life situations that involve proportions, ratios, and quantitative analysis. Remember to practice regularly to strengthen your understanding and build confidence in tackling percentage problems. With consistent effort, you'll become proficient in working with percentages and fractions, making them valuable tools in your mathematical toolkit.
Latest Posts
Latest Posts
-
How Many Pounds 15 Kg
Sep 13, 2025
-
How Much Is Mcdonalds Tax
Sep 13, 2025
-
1 Divided By 1 2
Sep 13, 2025
-
What Time Is 20 30
Sep 13, 2025
-
1 And 1 2 Inches
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 13 Out Of 20 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.