1 Divided By 1 2
saludintensiva
Sep 13, 2025 · 6 min read
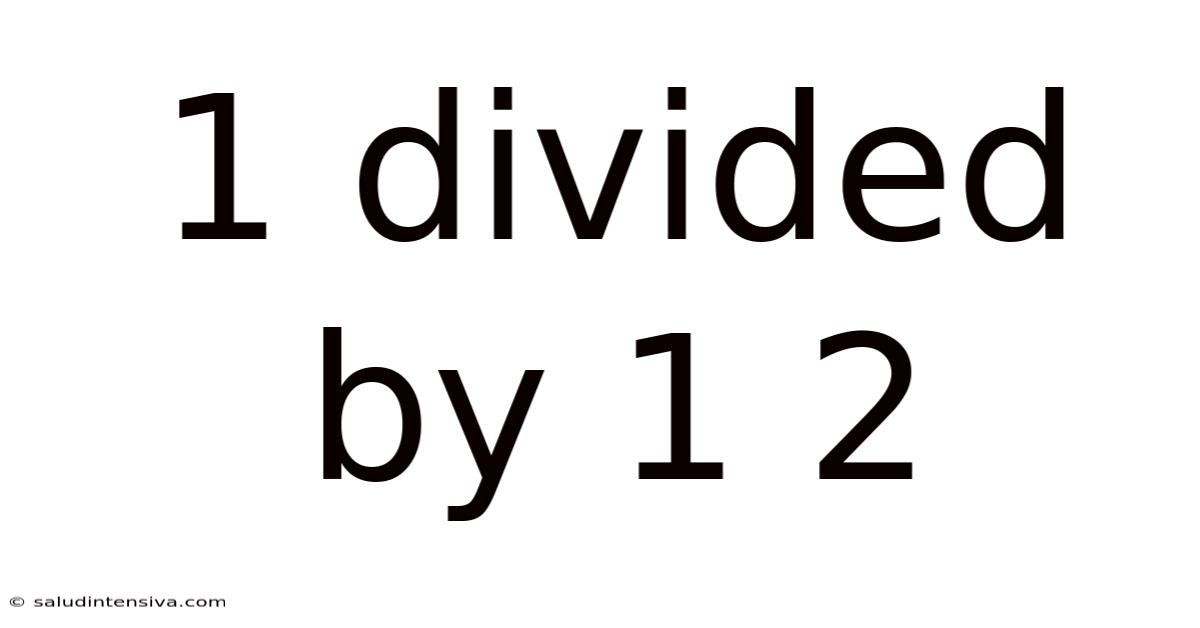
Table of Contents
Unraveling the Mystery: 1 Divided by 1/2 (and Why It's Not What You Think)
Have you ever encountered a simple math problem that unexpectedly stumped you? Many people find themselves momentarily confused when faced with the question: what is 1 divided by 1/2? While the answer might seem counterintuitive at first glance, understanding the underlying principles of fraction division reveals a surprisingly elegant solution. This article will delve into the intricacies of this seemingly simple problem, exploring the mathematical concepts involved and offering a clear, step-by-step explanation. We'll unpack the reasoning behind the answer, address common misconceptions, and even touch upon the broader applications of fraction division in everyday life. By the end, you'll not only know the answer but also possess a deeper understanding of fraction arithmetic.
Understanding Fraction Division: A Foundation
Before tackling 1 divided by 1/2, it's crucial to establish a solid understanding of fraction division in general. Unlike addition and subtraction, where we often find common denominators, division with fractions involves a slightly different approach – we invert (or reciprocate) the second fraction and then multiply. This "invert and multiply" method is the cornerstone of fraction division, and mastering it unlocks the solution to many seemingly complex problems.
Let's consider a simpler example: 2/3 divided by 1/4. The steps are as follows:
-
Invert the second fraction: The reciprocal of 1/4 is 4/1 (or simply 4).
-
Multiply the first fraction by the inverted second fraction: (2/3) * (4/1) = 8/3.
-
Simplify (if possible): In this case, 8/3 is an improper fraction, which can be expressed as a mixed number: 2 and 2/3.
This "invert and multiply" method isn't just a trick; it's derived from the fundamental definition of division. When we divide by a fraction, we're essentially asking: "How many times does this fraction fit into the first number?" Inverting and multiplying provides the mathematical framework for answering this question accurately.
Solving the Puzzle: 1 Divided by 1/2
Now, let's apply this knowledge to the problem at hand: 1 divided by 1/2.
-
Rewrite the whole number as a fraction: To maintain consistency, let's express 1 as a fraction: 1/1.
-
Invert the second fraction: The reciprocal of 1/2 is 2/1 (or simply 2).
-
Multiply the fractions: (1/1) * (2/1) = 2/1.
-
Simplify: 2/1 simplifies to 2.
Therefore, the answer to 1 divided by 1/2 is 2.
This might seem counterintuitive. After all, we're dividing, and yet the answer is larger than the number we started with. This is because dividing by a fraction less than 1 actually results in a larger number. Think of it this way: if you divide a pizza into halves, you have two halves. Therefore, one whole pizza contains two half-pizzas.
Visualizing the Solution
Visual aids can often clarify abstract mathematical concepts. Imagine you have one whole pizza (represented by the number 1). If you want to know how many half pizzas are in one whole pizza, you would divide the whole pizza into halves. You'd find that there are two halves, hence the answer of 2.
This visual representation helps connect the abstract mathematical operation to a tangible, real-world scenario, making the concept more intuitive and easier to grasp.
Addressing Common Misconceptions
Many people initially struggle with fraction division because they try to apply the same rules as whole number division. This often leads to incorrect answers. Here are some common misconceptions to avoid:
-
Incorrectly subtracting fractions: Some might mistakenly try to subtract 1/2 from 1, leading to an incorrect answer of 1/2. Remember, division is not subtraction.
-
Forgetting to invert: A common error is to forget to invert the second fraction before multiplying. This results in an incorrect answer. Always remember the crucial step of inverting the divisor (the fraction you're dividing by).
-
Misunderstanding the meaning of division: The fundamental concept of division—how many times one number fits into another—needs to be understood clearly, especially when dealing with fractions.
Beyond the Basics: Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept confined to textbooks. It finds practical applications in numerous everyday situations:
-
Cooking and Baking: Many recipes require precise measurements, often involving fractions. Dividing a recipe to serve fewer people necessitates fraction division. For example, if a recipe calls for 2/3 cup of flour and you only want to make half the recipe, you'd need to calculate 2/3 divided by 2 (or multiplied by 1/2).
-
Sewing and Crafting: Cutting fabric or other materials often involves precise measurements, making fraction division essential.
-
Construction and Engineering: Precise calculations involving lengths, volumes, and areas are crucial in construction and engineering, and these often involve fractions and the need for division.
-
Financial Calculations: Dividing shares or calculating interest rates may involve fractional numbers, requiring an understanding of fraction division for accurate calculations.
-
Data Analysis: In fields like statistics and data analysis, handling data often involves fractions, and the ability to perform fraction division efficiently is essential.
Frequently Asked Questions (FAQ)
Q: Why do we invert and multiply when dividing fractions?
A: The "invert and multiply" rule is derived from the definition of division. Dividing by a fraction is equivalent to multiplying by its reciprocal. This stems from the mathematical properties of fractions and their multiplicative inverses.
Q: Can I use a calculator to solve this type of problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for developing mathematical proficiency and problem-solving skills.
Q: What if the numbers involved are more complex fractions?
A: The same principle applies. Invert the second fraction and multiply. Simplify the result, converting improper fractions to mixed numbers if necessary.
Q: What if I'm dividing by a whole number?
A: You can treat a whole number as a fraction with a denominator of 1. For example, dividing by 3 is the same as dividing by 3/1. Then, follow the "invert and multiply" rule.
Conclusion: Mastering Fraction Division
The seemingly simple problem of 1 divided by 1/2 reveals a wealth of mathematical concepts. Mastering fraction division isn't just about getting the right answer; it's about building a solid foundation in arithmetic, understanding the underlying principles, and appreciating the practical applications of these concepts in the real world. By applying the "invert and multiply" method and understanding the logic behind it, you can confidently tackle any fraction division problem you encounter. Remember, practice is key; the more you work with fractions, the more comfortable and confident you'll become. So grab a pencil and paper, and start practicing! You'll be surprised at how quickly your understanding grows. Remember, even seemingly simple problems can unlock a deeper understanding of mathematical principles when approached with curiosity and a willingness to learn.
Latest Posts
Latest Posts
-
0 25 Acres In Square Feet
Sep 13, 2025
-
6 5 As A Percentage
Sep 13, 2025
-
22 9 As A Decimal
Sep 13, 2025
-
Round To The Nearest 10000
Sep 13, 2025
-
What Was 120 Days Ago
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.