6 5 As A Percentage
saludintensiva
Sep 13, 2025 · 5 min read
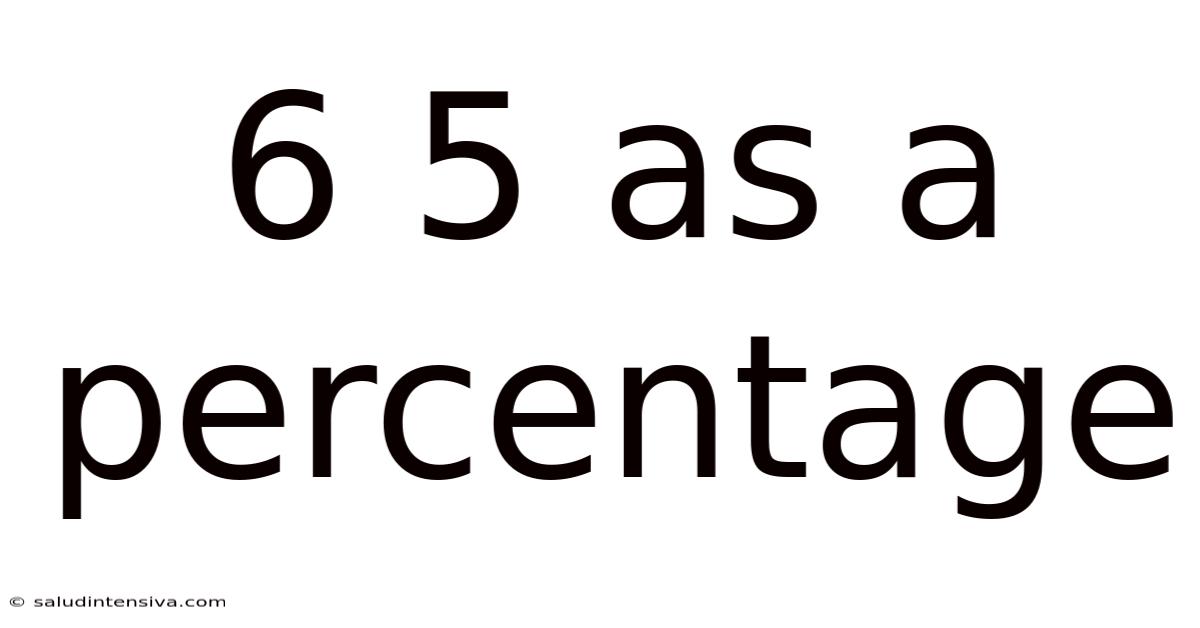
Table of Contents
Understanding 6/5 as a Percentage: A Comprehensive Guide
What does 6/5 as a percentage mean? This seemingly simple question delves into the fundamental concepts of fractions, decimals, and percentages – crucial components of mathematics used daily in various aspects of life, from calculating discounts to understanding financial reports. This article will provide a thorough explanation of how to convert 6/5 into a percentage, exploring the underlying principles and offering practical applications. We'll cover the step-by-step process, delve into the mathematical reasoning behind the conversion, and answer frequently asked questions to ensure a complete understanding of this important concept.
Understanding Fractions, Decimals, and Percentages
Before jumping into the conversion, let's solidify our understanding of the three key concepts: fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 6/5, 6 is the numerator and 5 is the denominator. This indicates that we have 6 parts out of a total of 5 parts. This is an improper fraction because the numerator is larger than the denominator.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the decimal point separating the whole number from the fractional part. For instance, 1.5 is a decimal representing one and a half.
-
Percentages: Percentages represent parts of a whole as a fraction of 100. The symbol "%" is used to denote a percentage. For example, 50% means 50 parts out of 100, which is equivalent to ½ or 0.5.
Converting 6/5 to a Percentage: A Step-by-Step Guide
Converting 6/5 to a percentage involves a two-step process:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, you divide the numerator by the denominator. In this case:
6 ÷ 5 = 1.2
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
1.2 x 100 = 120
Therefore, 6/5 as a percentage is 120%.
Mathematical Explanation: Why 120%?
The result of 120% might seem counterintuitive at first. After all, we're used to percentages being between 0% and 100%. However, remember that 6/5 is an improper fraction, meaning it represents more than one whole. Think of it this way:
- If you have 5/5, that's one whole (100%).
- 6/5 means you have one whole (5/5) and an additional 1/5.
- 1/5 as a decimal is 0.2 (1 ÷ 5 = 0.2).
- 0.2 as a percentage is 20% (0.2 x 100 = 20%).
Therefore, 6/5 represents 100% + 20% = 120%.
Practical Applications of Understanding 6/5 as a Percentage
Understanding the conversion of 6/5 to 120% has practical implications across various fields:
-
Finance: Calculating interest rates, profit margins, or investment returns often involves working with percentages exceeding 100%. For example, if an investment grows by 6/5 of its initial value, it has increased by 120%.
-
Business: Analyzing sales figures, comparing growth rates, or evaluating performance metrics frequently requires converting fractions or decimals to percentages. A 120% increase in sales indicates substantial growth.
-
Science: In scientific experiments or data analysis, representing data as percentages is often necessary for easy interpretation and comparison. A 120% increase in a measured quantity signifies a significant change.
-
Everyday Life: Even everyday tasks like calculating tips or discounts can involve working with percentages. Understanding how to convert fractions to percentages allows for quick and accurate calculations.
Different Ways to Express the Same Value
It's important to recognize that 6/5, 1.2, and 120% all represent the same quantity. The choice of which representation to use depends on the context and the desired level of precision. Fractions offer clarity in representing the exact ratio, while decimals are useful for calculations, and percentages provide an easily understandable representation of the relative magnitude.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted into percentages?
A: Yes, all fractions can be converted to percentages by following the steps outlined above: dividing the numerator by the denominator to obtain a decimal and then multiplying the decimal by 100 to obtain the percentage.
Q: What if the fraction is a mixed number (e.g., 1 1/5)?
A: First, convert the mixed number to an improper fraction. In this example, 1 1/5 becomes (1 x 5 + 1)/5 = 6/5. Then, follow the steps outlined above to convert the improper fraction to a percentage.
Q: What does it mean if a percentage is greater than 100%?
A: A percentage greater than 100% indicates a value that is more than the whole. It signifies an increase or growth exceeding the initial value.
Q: How can I practice converting fractions to percentages?
A: Practice is key! Try converting various fractions (both proper and improper) to percentages. You can find practice exercises online or in textbooks. Start with simple fractions and gradually move on to more complex ones. Understanding the underlying principles is more important than memorizing specific conversions.
Q: Are there any online calculators that can help with this conversion?
A: Yes, many online calculators are available that can convert fractions to percentages. Simply search for "fraction to percentage calculator" on a search engine. However, understanding the process is crucial for solving problems effectively without relying solely on calculators.
Conclusion
Converting 6/5 to a percentage, resulting in 120%, is a straightforward process involving converting the fraction to a decimal and then to a percentage. This seemingly simple conversion demonstrates the interconnectedness of fractions, decimals, and percentages, which are fundamental concepts in mathematics with widespread practical applications in various aspects of life. By understanding the underlying principles and practicing the conversion process, you can confidently tackle similar problems and apply this knowledge to various real-world situations. Remember, the ability to seamlessly transition between these mathematical representations empowers you to interpret and analyze data effectively, whether you're managing finances, analyzing scientific data, or simply tackling everyday calculations.
Latest Posts
Latest Posts
-
19 20 In Decimal Form
Sep 13, 2025
-
Gcf Of 10 And 30
Sep 13, 2025
-
What Is 12 15 Simplified
Sep 13, 2025
-
2 3 To The Third Power
Sep 13, 2025
-
Whats 625 As A Fraction
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.