What Is 12 15 Simplified
saludintensiva
Sep 13, 2025 · 5 min read
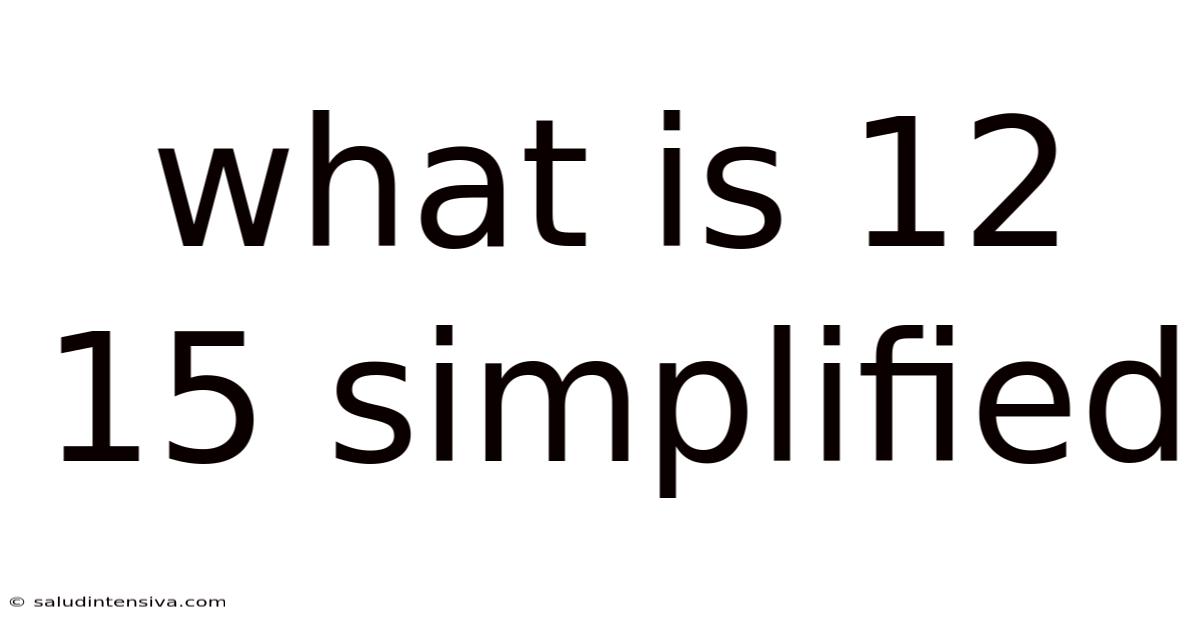
Table of Contents
What is 12/15 Simplified? Understanding Fractions and Their Simplification
This article will explore the simplification of the fraction 12/15, delving into the fundamental concepts of fractions, greatest common divisors (GCD), and how to reduce fractions to their simplest form. We will cover the process step-by-step, explain the underlying mathematical principles, and answer frequently asked questions regarding fraction simplification. This guide is designed for anyone wanting to improve their understanding of fractions, from students brushing up on their math skills to anyone seeking a refresher on fundamental arithmetic. Understanding fraction simplification is crucial for various mathematical applications and everyday problem-solving.
Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 12/15, 12 is the numerator, and 15 is the denominator. This means we have 12 parts out of a possible 15 equal parts.
Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. To do this, we need to find the greatest common divisor (GCD), also known as the highest common factor (HCF), of both the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
There are several ways to find the GCD:
-
Listing Factors: List all the factors (numbers that divide evenly) of both the numerator (12) and the denominator (15). Then, identify the largest factor they have in common.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 15: 1, 3, 5, 15
The largest common factor is 3.
-
Prime Factorization: This method involves breaking down both numbers into their prime factors (numbers divisible only by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power.
Prime factorization of 12: 2 x 2 x 3 = 2² x 3 Prime factorization of 15: 3 x 5
The common prime factor is 3. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
15 ÷ 12 = 1 with a remainder of 3 12 ÷ 3 = 4 with a remainder of 0
The last non-zero remainder is 3, so the GCD is 3.
Simplifying 12/15
Now that we've established that the GCD of 12 and 15 is 3, we can simplify the fraction:
-
Divide both the numerator and the denominator by the GCD:
12 ÷ 3 = 4 15 ÷ 3 = 5
-
The simplified fraction is:
4/5
Therefore, 12/15 simplified is 4/5. This means that 12/15 and 4/5 represent the same value; they are equivalent fractions.
Visual Representation
Imagine a pizza cut into 15 slices. 12/15 represents having 12 of those slices. If we group the slices into sets of 3, we have 4 sets of 3 slices out of a total of 5 sets of 3 slices. This visually demonstrates the equivalence of 12/15 and 4/5.
Explanation of the Mathematical Principle
The process of simplifying fractions relies on the fundamental property of fractions: multiplying or dividing both the numerator and the denominator by the same non-zero number does not change the value of the fraction. By dividing both by the GCD, we are essentially canceling out the common factors, leaving the fraction in its simplest form. This is based on the associative and commutative properties of multiplication and division.
Practical Applications
Simplifying fractions is essential in various areas:
-
Everyday Calculations: When dealing with portions, measurements, or ratios in everyday life, simplifying fractions makes the results easier to understand and use.
-
Algebra: Simplifying fractions is crucial for performing algebraic operations like adding, subtracting, multiplying, and dividing fractions.
-
Geometry: Fractions frequently appear in geometric calculations involving areas, volumes, and ratios of lengths.
-
Physics and Engineering: Fractions are fundamental in various physics and engineering calculations, and simplifying them helps to streamline the calculations and interpret the results more efficiently.
Frequently Asked Questions (FAQ)
-
What if the GCD is 1? If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form and cannot be simplified further.
-
Can I simplify fractions with decimals? No, you need to convert the decimals to fractions before simplifying.
-
What if the fraction is negative? The simplification process remains the same. The negative sign remains with the simplified fraction. For example, -12/15 simplifies to -4/5.
-
Are there online calculators for simplifying fractions? Yes, many online calculators can simplify fractions quickly and efficiently. However, understanding the underlying process is crucial for building mathematical proficiency.
-
Why is simplifying fractions important? Simplifying fractions makes them easier to work with and understand. It allows for simpler calculations and clearer interpretations of results.
Further Exploration
To deepen your understanding, try practicing with different fractions. Start with simpler fractions and gradually work towards more complex ones. You can also explore the concept of improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction). Understanding these concepts will provide a comprehensive grasp of fraction manipulation.
Conclusion
Simplifying fractions, as demonstrated with the example of 12/15, is a fundamental mathematical skill with wide-ranging applications. By understanding the concept of the greatest common divisor (GCD) and applying the appropriate method, you can efficiently reduce fractions to their simplest form. This process relies on the core principles of fraction equivalence and the properties of numbers. Mastering fraction simplification is not merely about getting the right answer; it's about developing a deeper understanding of fundamental mathematical concepts and their practical applications in various fields. Regular practice and exploration of related concepts will further enhance your mathematical abilities and problem-solving skills. Remember, the key is to not just know the method, but to understand why it works.
Latest Posts
Latest Posts
-
90 Degrees C To F
Sep 13, 2025
-
Lcm Of 14 And 49
Sep 13, 2025
-
58 Minutes Ago From Now
Sep 13, 2025
-
Find The Value Of 2abcosc
Sep 13, 2025
-
50 Deg C To Fahrenheit
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 15 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.