1 1 2 3 4
saludintensiva
Sep 19, 2025 · 7 min read
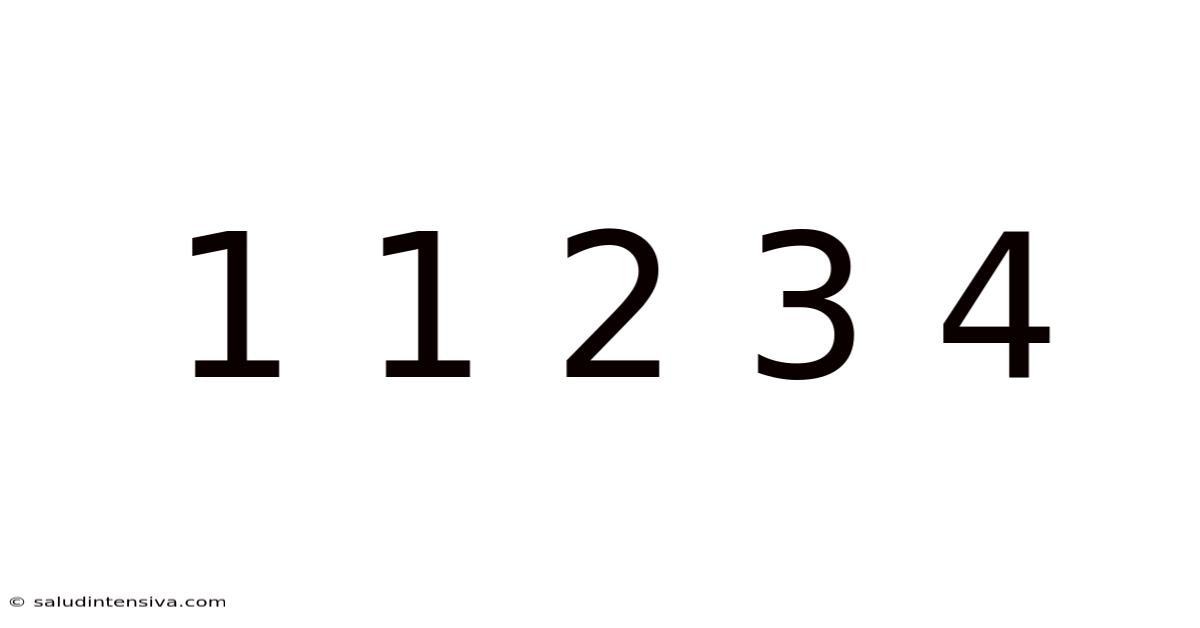
Table of Contents
Unraveling the Sequence: 1 1 2 3 5... and Beyond
The seemingly simple sequence 1, 1, 2, 3, 5… might appear innocuous at first glance. However, this numerical progression, known as the Fibonacci sequence, holds a captivating history, profound mathematical significance, and astonishing applications across various scientific fields. This article will delve into the fascinating world of the Fibonacci sequence, exploring its origins, mathematical properties, and surprising appearances in nature, art, and even computer science. We will unravel its secrets, step-by-step, making this complex subject accessible to everyone.
Introduction: A Glimpse into the Golden Ratio
The Fibonacci sequence is defined by the simple recursive relation where each number is the sum of the two preceding ones: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, and so on. The sequence continues indefinitely: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and beyond. While seemingly straightforward, this sequence reveals a deeper connection to the golden ratio, approximately 1.618, denoted by the Greek letter phi (Φ). As the Fibonacci numbers get larger, the ratio of consecutive numbers approaches the golden ratio. For instance, 55/34 ≈ 1.618 and 89/55 ≈ 1.618. This connection to the golden ratio is a key to understanding the sequence's profound influence on various aspects of the natural world and artistic endeavors.
A Journey Through History: From Rabbits to Mathematics
While the sequence bears the name of Leonardo Pisano, better known as Fibonacci (circa 1170-1250), its presence can be traced back even further. Indian mathematicians explored similar patterns centuries before Fibonacci. However, it was Fibonacci's Liber Abaci (Book of Calculation), published in 1202, that introduced the sequence to the Western world through a problem involving the growth of a rabbit population. The problem posited that a pair of rabbits, starting with one pair, produces a new pair each month, with each new pair becoming reproductive after one month. This seemingly simple problem elegantly unfolds the Fibonacci sequence, where each number represents the total number of rabbit pairs at the end of each month. This historical context highlights the sequence's intuitive origins and its potential to model natural phenomena.
Mathematical Properties: Delving Deeper into the Sequence
The Fibonacci sequence possesses numerous fascinating mathematical properties. Let's explore some key characteristics:
-
Recursive Definition: As mentioned earlier, the core defining characteristic is its recursive nature: F<sub>n</sub> = F<sub>n-1</sub> + F<sub>n-2</sub>, where F<sub>n</sub> represents the nth Fibonacci number, with F<sub>0</sub> = 0 and F<sub>1</sub> = 1. This simple rule generates the entire sequence.
-
Closed-Form Expression (Binet's Formula): While the recursive definition is elegant, it's computationally inefficient for larger numbers. Binet's formula provides a direct calculation:
F<sub>n</sub> = (Φ<sup>n</sup> - ψ<sup>n</sup>) / √5
where Φ is the golden ratio (approximately 1.618) and ψ is its conjugate (approximately -0.618). This formula, although seemingly complex, allows for the direct calculation of any Fibonacci number without iterating through the sequence.
-
Relationship with the Golden Ratio: As previously stated, the ratio of consecutive Fibonacci numbers approaches the golden ratio as n approaches infinity. This relationship forms the basis for the sequence's appearance in various natural phenomena exhibiting golden ratio proportions.
-
Summation Properties: Various summation formulas exist, revealing interesting patterns within the sequence. For example, the sum of the first n Fibonacci numbers is equal to F<sub>n+2</sub> - 1.
-
Even and Odd Numbers: Observe the pattern of even and odd numbers within the sequence. Every third Fibonacci number is even, and the rest are odd.
The Fibonacci Sequence in Nature: A Tapestry of Mathematical Beauty
The ubiquity of the Fibonacci sequence in nature is perhaps its most compelling aspect. Its presence showcases the underlying mathematical order governing the natural world. Here are some striking examples:
-
Flower Petals: Many flowers exhibit a number of petals that corresponds to a Fibonacci number: lilies (3 petals), buttercups (5 petals), daisies (34, 55, or even 89 petals). This pattern suggests an underlying optimization principle in the flower's growth and arrangement.
-
Seed Heads: The arrangement of seeds in a sunflower head, or the scales on a pine cone, follows a spiral pattern. Counting the spirals in opposite directions often reveals consecutive Fibonacci numbers. This spiral arrangement maximizes the number of seeds or scales that can fit within a limited space.
-
Tree Branches: The branching patterns of trees often exhibit Fibonacci numbers. The number of branches at each level of the tree can frequently be found within the Fibonacci sequence, reflecting the tree's growth pattern.
-
Leaf Arrangement (Phyllotaxis): The arrangement of leaves around a stem (phyllotaxis) also often displays Fibonacci numbers in the number of leaves per turn around the stem. This pattern ensures that each leaf gets optimal sunlight exposure.
-
Seashells: The spiral shape of many seashells, like the nautilus shell, approximates a logarithmic spiral, whose growth factor is related to the golden ratio and therefore the Fibonacci sequence. This spiral shape is efficient for growth and structural integrity.
Beyond Nature: Applications in Art, Architecture, and Computer Science
The influence of the Fibonacci sequence extends far beyond the natural world. Its aesthetic appeal and mathematical properties have found applications in art, architecture, and even computer science:
-
Art and Architecture: The golden ratio, intrinsically linked to the Fibonacci sequence, has been used by artists and architects for centuries to create aesthetically pleasing proportions. The Parthenon, Leonardo da Vinci's paintings (including the Mona Lisa), and many other works of art and architecture incorporate golden ratio proportions, creating a sense of balance and harmony.
-
Music: The Fibonacci sequence and the golden ratio appear in musical compositions, influencing the placement of musical phrases, the development of themes, and the overall structure of a piece. The proportions often create a sense of natural flow and progression.
-
Computer Science: The Fibonacci sequence appears in various algorithms and data structures in computer science, including search algorithms and dynamic programming solutions. Its recursive nature provides a foundation for efficient computation in certain scenarios. The Fibonacci sequence can also be used in modeling various aspects of computer networks, such as the routing of data packets.
Frequently Asked Questions (FAQ)
-
Is the Fibonacci sequence infinite? Yes, the Fibonacci sequence is infinite. The recursive definition allows for the generation of an unlimited number of terms.
-
What is the significance of the golden ratio? The golden ratio is approximately 1.618 and is intimately connected to the Fibonacci sequence. As the Fibonacci numbers increase, the ratio of consecutive numbers approaches the golden ratio. This ratio is considered aesthetically pleasing and appears in many natural and artistic contexts.
-
Are there any other similar sequences? Yes, there are many other similar sequences, such as the Lucas numbers, which are closely related to the Fibonacci numbers.
-
Can the Fibonacci sequence be used to predict future events? No, the Fibonacci sequence is a mathematical tool for understanding patterns. It is not a predictive tool for future events. Its appearance in various natural phenomena suggests inherent underlying patterns, not future predictions.
-
Why is the Fibonacci sequence so prevalent in nature? The precise reason for the prevalence of the Fibonacci sequence in nature is still a subject of ongoing research. However, it is generally believed to represent an efficient and optimal way for organisms to grow and arrange themselves in space, maximizing resource utilization and survival chances.
Conclusion: The Enduring Allure of the Fibonacci Sequence
The Fibonacci sequence, a deceptively simple numerical progression, unveils a world of mathematical wonder and natural beauty. From its humble beginnings in a rabbit problem to its profound influence on various scientific fields, its enduring legacy lies in its ability to connect seemingly disparate aspects of our world. Its presence in nature showcases the inherent order and efficiency found in the natural world, reminding us of the underlying mathematical principles that govern our existence. The ongoing exploration of the Fibonacci sequence continues to inspire mathematicians, scientists, and artists alike, demonstrating its timeless relevance and enduring allure. The simple sequence 1, 1, 2, 3, 5… continues to be a testament to the power and elegance of mathematics and its profound influence on our understanding of the world around us.
Latest Posts
Latest Posts
-
What Does 1 2 Equal
Sep 19, 2025
-
Sum Of Squares Between Calculator
Sep 19, 2025
-
Gcf Of 16 And 32
Sep 19, 2025
-
Gcf Of 28 And 14
Sep 19, 2025
-
4 9 As A Percentage
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.