Gcf Of 28 And 14
saludintensiva
Sep 19, 2025 · 6 min read
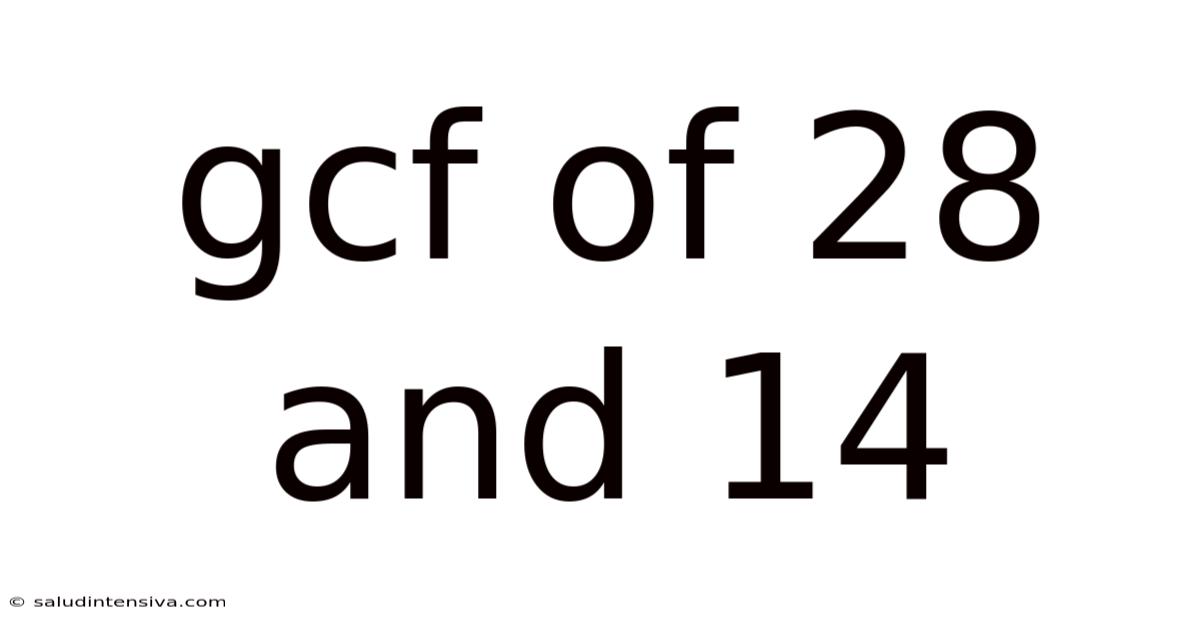
Table of Contents
Unveiling the Greatest Common Factor: A Deep Dive into GCF(28, 14)
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical applications. This article delves deep into calculating the GCF of 28 and 14, exploring various methods, their theoretical underpinnings, and practical applications. Whether you're a student brushing up on your math skills or an educator seeking enriching material, this comprehensive guide will provide a solid foundation in understanding GCF and its significance.
Introduction: What is a Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both (or all) numbers in a set. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and even exploring more advanced mathematical concepts. This article focuses on finding the GCF of 28 and 14, illustrating different approaches and expanding upon the core principles.
Method 1: Prime Factorization
This method is a fundamental and reliable way to find the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 28
28 can be broken down as follows:
28 = 2 x 14 = 2 x 2 x 7 = 2² x 7
Step 2: Prime Factorization of 14
14's prime factorization is:
14 = 2 x 7
Step 3: Identifying Common Factors
Now, we compare the prime factorizations of 28 and 14:
28 = 2² x 7 14 = 2 x 7
Both numbers share a factor of 2 and a factor of 7.
Step 4: Calculating the GCF
To find the GCF, we multiply the common prime factors:
GCF(28, 14) = 2 x 7 = 14
Therefore, the greatest common factor of 28 and 14 is 14.
Method 2: Listing Factors
This method is more intuitive for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Step 1: Factors of 28
The factors of 28 are 1, 2, 4, 7, 14, and 28.
Step 2: Factors of 14
The factors of 14 are 1, 2, 7, and 14.
Step 3: Identifying Common Factors
Comparing the lists, we find the common factors: 1, 2, 7, and 14.
Step 4: Determining the GCF
The largest common factor is 14. Therefore, GCF(28, 14) = 14.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. We repeatedly apply the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Step 1: Divide the Larger Number by the Smaller Number
Divide 28 by 14:
28 ÷ 14 = 2 with a remainder of 0.
Step 2: Interpret the Result
Since the remainder is 0, the smaller number (14) is the GCF.
Therefore, GCF(28, 14) = 14.
Understanding the Significance of GCF
The GCF plays a vital role in various mathematical operations and applications:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For example, the fraction 28/14 can be simplified to 2/1 (or simply 2) by dividing both the numerator and denominator by their GCF, which is 14.
-
Solving Equations: GCF is used in solving Diophantine equations, a type of equation where solutions are restricted to integers.
-
Algebraic Expressions: Finding the GCF is crucial for factoring algebraic expressions, making them easier to manipulate and solve. For instance, consider the expression 28x + 14y. The GCF of 28 and 14 is 14, so we can factor the expression as 14(2x + y).
-
Geometry and Measurement: GCF is used in geometric problems involving finding the largest square tile that can perfectly cover a rectangular area. If the rectangle has dimensions 28 units by 14 units, the largest square tile would have a side length of 14 units.
-
Number Theory: GCF is a cornerstone concept in number theory, a branch of mathematics that studies the properties of integers. It’s used in many theorems and proofs related to divisibility and prime numbers.
GCF and Least Common Multiple (LCM)
The GCF and the least common multiple (LCM) are closely related concepts. The LCM is the smallest positive integer that is a multiple of both (or all) numbers in a set. For any two positive integers a and b, the product of their GCF and LCM is equal to the product of the two numbers. This relationship is expressed as:
GCF(a, b) x LCM(a, b) = a x b
In our case:
GCF(28, 14) x LCM(28, 14) = 28 x 14
14 x LCM(28, 14) = 392
LCM(28, 14) = 392 / 14 = 28
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, let's find the GCF of 28, 14, and 42.
Method 1: Prime Factorization
- 28 = 2² x 7
- 14 = 2 x 7
- 42 = 2 x 3 x 7
The common prime factors are 2 and 7. Therefore, GCF(28, 14, 42) = 2 x 7 = 14.
Method 2: Euclidean Algorithm (for multiple numbers)
The Euclidean algorithm can be extended to multiple numbers by finding the GCF of two numbers at a time, iteratively. First find the GCF of 28 and 14 (which is 14). Then find the GCF of 14 and 42 (which is 14).
Frequently Asked Questions (FAQ)
Q1: Is the GCF always smaller than the numbers involved?
A1: Yes, the GCF is always less than or equal to the smallest number in the set. If the numbers are relatively prime (meaning their GCF is 1), the GCF will be 1.
Q2: Can the GCF be a negative number?
A2: No, the GCF is always a positive integer. We're concerned with the magnitude of the common divisor, not its sign.
Q3: What if the numbers are very large?
A3: For very large numbers, the Euclidean algorithm is the most efficient method. Computer programs and calculators readily implement this algorithm for quick computation.
Q4: What are some real-world applications of GCF besides those mentioned?
A4: GCF finds applications in cryptography, scheduling problems (finding the least common time interval for events), and data compression algorithms.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill in mathematics with wide-ranging applications. We've explored three different methods – prime factorization, listing factors, and the Euclidean algorithm – each providing a unique approach to solving this problem. Understanding the GCF not only helps in simplifying calculations but also provides a deeper understanding of number theory and its practical relevance across various disciplines. Whether you're a student, teacher, or simply someone curious about mathematics, mastering the concept of GCF opens doors to further mathematical exploration and problem-solving. The ability to efficiently determine the GCF of any set of numbers is a valuable asset in your mathematical toolbox. Remember that the choice of method depends on the context and the size of the numbers involved. The Euclidean algorithm stands out for its efficiency, especially with larger numbers, while prime factorization offers a more intuitive understanding of the underlying principles. Through consistent practice and application, you can gain proficiency in this fundamental mathematical concept.
Latest Posts
Latest Posts
-
32 9 As A Mixed Number
Sep 19, 2025
-
Square Root Of X 9
Sep 19, 2025
-
Round To The Greatest Place
Sep 19, 2025
-
How Long Is 325 Minutes
Sep 19, 2025
-
91 Degrees Fahrenheit To Celsius
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 28 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.