Square Root Of X 9
saludintensiva
Sep 19, 2025 · 6 min read
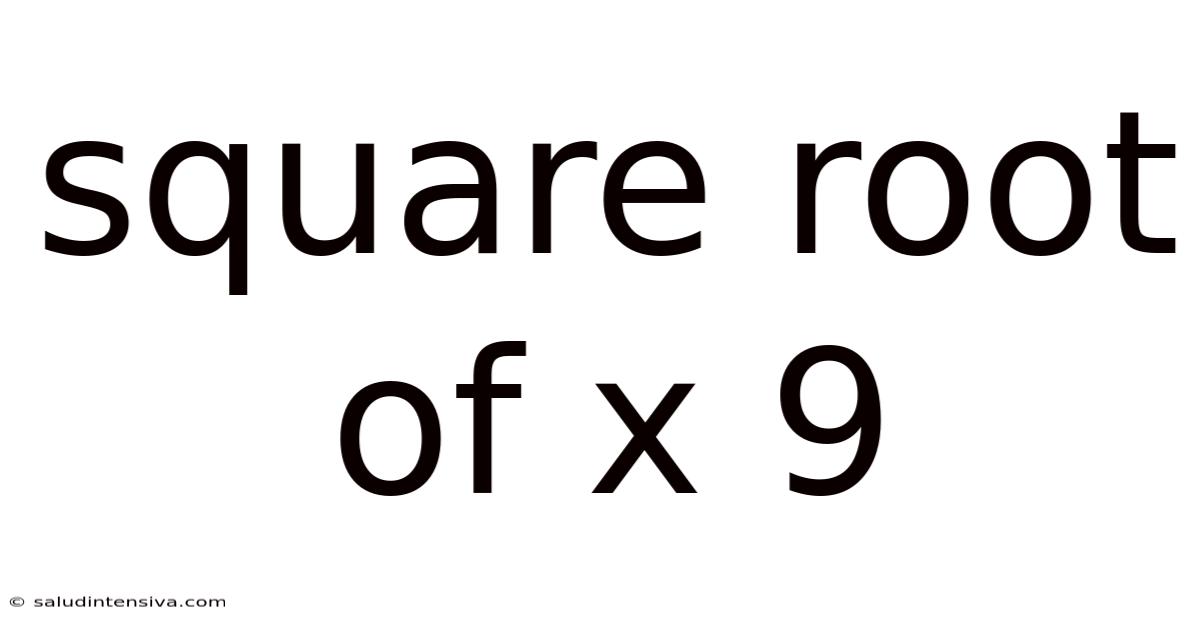
Table of Contents
Understanding the Square Root of x + 9: A Comprehensive Guide
Finding the square root of x + 9 might seem like a simple algebraic task, but understanding its implications and applications goes far beyond just the mechanics of calculation. This comprehensive guide will delve into the intricacies of this mathematical concept, exploring its various aspects, from basic calculations to advanced applications and potential pitfalls. We’ll cover everything you need to know, whether you're a high school student brushing up on your algebra or a more advanced learner looking to solidify your understanding.
Introduction: What is a Square Root?
Before tackling the square root of x + 9, let's establish a firm understanding of what a square root represents. In simple terms, the square root of a number is a value that, when multiplied by itself (squared), equals the original number. For instance, the square root of 25 is 5 because 5 x 5 = 25. Mathematically, we represent the square root using the radical symbol: √. Therefore, √25 = 5.
It's crucial to remember that every positive number has two square roots: a positive and a negative one. While √25 = 5, it's also true that (-5) x (-5) = 25. However, the principal square root (the one typically given) is always the positive value.
Calculating the Square Root of x + 9: A Step-by-Step Approach
The expression √(x + 9) represents the square root of the quantity (x + 9). Unlike finding the square root of a constant number, this involves a variable, 'x'. This means the value of the square root will depend on the value assigned to 'x'. There's no single numerical answer; instead, we simplify and analyze the expression.
Let's consider different scenarios:
Scenario 1: Solving for x when the square root is known.
Suppose we know that √(x + 9) = 5. To solve for x, we follow these steps:
-
Square both sides: Squaring both sides of the equation eliminates the square root: (√(x + 9))² = 5² This simplifies to x + 9 = 25.
-
Isolate x: Subtract 9 from both sides: x = 25 - 9 = 16.
Therefore, if the square root of (x + 9) equals 5, then x equals 16.
Scenario 2: Simplifying the expression.
Often, you might be asked to simplify √(x + 9) without knowing the value of x. In this case, simplification depends on the context. If x is a perfect square plus 9 (meaning x+9 is a perfect square), further simplification is possible. For example, if x=7, then √(7+9) = √16 = 4. However, if x=2, √(2+9) = √11 which can't be simplified further without using approximations.
Scenario 3: Working with inequalities.
You might encounter problems involving inequalities, such as finding the values of x for which √(x + 9) > 3. To solve this:
-
Square both sides: (√(x + 9))² > 3² This results in x + 9 > 9.
-
Isolate x: Subtract 9 from both sides: x > 0.
This inequality means that √(x + 9) will be greater than 3 for any value of x greater than 0.
The Domain of √(x + 9)
The domain of a function refers to the set of all possible input values (in this case, values of x) for which the function is defined. With square roots, we need to ensure that the expression inside the radical (the radicand) is non-negative because we cannot find the square root of a negative number within the real number system (we'd enter the realm of complex numbers).
Therefore, for √(x + 9) to be defined within the real numbers, the following condition must be met:
x + 9 ≥ 0
Solving for x: x ≥ -9
This means the domain of √(x + 9) is all real numbers greater than or equal to -9. Any value of x less than -9 will result in a negative radicand, leading to an undefined square root (in the real number system).
Graphical Representation
Visualizing the function y = √(x + 9) can provide further insight. The graph will be a portion of a parabola that opens to the right, starting at the point (-9, 0) and extending infinitely to the right and upward. This visual representation clearly demonstrates the domain restriction; the graph does not exist for x values less than -9.
Advanced Applications and Extensions
The concept of √(x + 9) extends beyond simple algebraic manipulation. It appears in various areas of mathematics and its applications:
-
Calculus: Derivatives and integrals involving square roots often include expressions similar to √(x + 9). Understanding its properties is crucial for solving these problems.
-
Physics: Many physical phenomena are modeled using square root functions. For example, the period of a simple pendulum involves a square root of a term related to length.
-
Engineering: Square root functions are frequently used in engineering calculations, particularly in areas involving mechanics, electricity, and fluid dynamics.
-
Statistics: Standard deviations and other statistical measures often involve square roots.
Frequently Asked Questions (FAQ)
Q: Can I simplify √(x + 9) further?
A: Only if (x + 9) is a perfect square. Otherwise, the expression is already in its simplest form within the real number system.
Q: What if x is negative?
A: If x is less than -9, the expression √(x + 9) is undefined within the real number system because the radicand becomes negative. However, it can be expressed using imaginary numbers (involving 'i', where i² = -1).
Q: How do I solve equations involving √(x + 9)?
A: Isolate the square root term, then square both sides of the equation. Always check your solution(s) to ensure they are valid within the domain of the original equation.
Q: What are the practical uses of understanding square roots like √(x + 9)?
A: Understanding square roots is fundamental to many fields, including solving equations, understanding functions, and modeling real-world phenomena in physics, engineering, and statistics. It forms the basis of more advanced mathematical concepts.
Conclusion: Mastering the Square Root of x + 9
Understanding the square root of x + 9 is not just about performing calculations; it’s about grasping the underlying principles of square roots, domains, and their applications in various fields. By understanding the domain restrictions, simplifying techniques, and solving equations involving this expression, you gain a deeper appreciation of algebraic manipulation and its practical significance. This knowledge provides a solid foundation for tackling more advanced mathematical concepts and real-world problems that utilize square roots. Remember to always consider the domain of the function to avoid errors and to ensure the validity of your solutions. Through consistent practice and a firm understanding of the concepts presented here, you can confidently handle any problem involving the square root of x + 9 and similar expressions.
Latest Posts
Latest Posts
-
10 Out Of 15 Percent
Sep 19, 2025
-
How Long Is 340 Minutes
Sep 19, 2025
-
16 7 As A Mixed Number
Sep 19, 2025
-
Equivalent Fractions For 14 16
Sep 19, 2025
-
Square Feet 1 4 Acre
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.