1 1 4 2 3
saludintensiva
Sep 14, 2025 · 6 min read
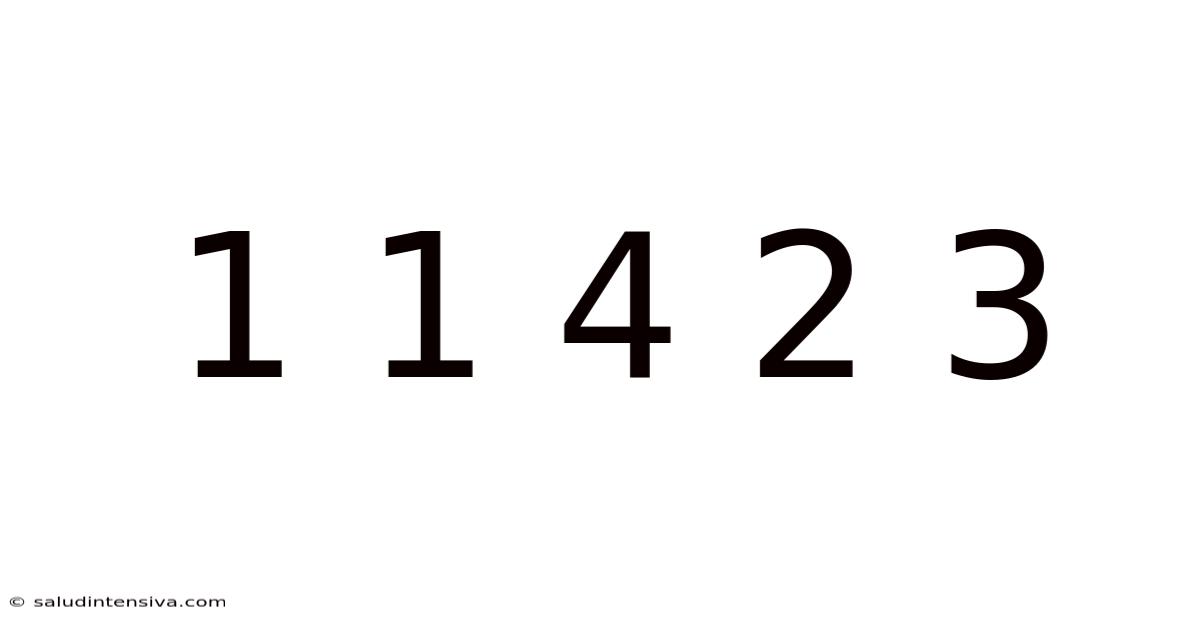
Table of Contents
Decoding the Sequence: Unraveling the Mysteries of 1 1 4 2 3
The seemingly simple sequence "1 1 4 2 3" might appear innocuous at first glance. However, this numerical puzzle hides a fascinating depth, prompting us to explore various mathematical and logical possibilities. This article delves into the potential patterns, underlying principles, and interpretations of this intriguing sequence, offering a journey into the world of number theory, pattern recognition, and creative problem-solving. We will explore several possible solutions, demonstrating that there’s often more than one way to approach a seemingly straightforward problem.
Introduction: The Allure of Numerical Sequences
Numerical sequences, like the enigmatic "1 1 4 2 3," have captivated mathematicians and puzzle enthusiasts for centuries. Their seemingly simple structure often belies a rich complexity, demanding insightful observation and analytical skills to decipher. The beauty of these sequences lies in their ability to reveal underlying patterns, showcasing the fundamental elegance and order within mathematics. This particular sequence, due to its brevity and ambiguity, allows for multiple interpretations, making it an excellent example to explore the various approaches to pattern recognition.
Potential Interpretations and Solutions
The lack of an immediately obvious pattern in "1 1 4 2 3" makes it particularly intriguing. Let's explore some potential interpretations:
1. A Look at Differences and Patterns:
One approach involves examining the differences between consecutive numbers in the sequence:
- 1 - 1 = 0
- 4 - 1 = 3
- 2 - 4 = -2
- 3 - 2 = 1
This difference sequence (0, 3, -2, 1) doesn't reveal an immediately clear pattern. However, we can analyze the second differences, which are the differences between the differences:
- 3 - 0 = 3
- -2 - 3 = -5
- 1 - (-2) = 3
Here, we observe a slight pattern: 3, -5, 3. While not immediately consistent, this could suggest a cyclical or oscillating behavior, possibly pointing towards a more complex underlying function generating the sequence. Further investigation might involve exploring higher-order differences or looking at other mathematical transformations.
2. Considering Prime Numbers and Factorials:
Let's examine the sequence in relation to prime numbers and factorials:
- 1: Not a prime number, 1! = 1
- 1: Not a prime number, 1! = 1
- 4: Not a prime number, 2! * 2 = 4
- 2: Prime number, 2! = 2
- 3: Prime number, 3! / 2 = 3
This approach highlights the presence of both prime numbers and factorial relationships. However, a consistent rule connecting all terms remains elusive. The connection between factorials and prime numbers could be explored more deeply using various mathematical functions, possibly revealing a hidden algorithm.
3. Exploring Number Bases and Representations:
Could the sequence be interpreted in a different number base? Let's consider base 2 (binary):
- 1 (decimal) = 1 (binary)
- 1 (decimal) = 1 (binary)
- 4 (decimal) = 100 (binary)
- 2 (decimal) = 10 (binary)
- 3 (decimal) = 11 (binary)
While the binary representations don't immediately reveal a clear pattern, further exploration with other number bases (base 3, base 4, etc.) could uncover hidden relationships. The inherent ambiguity of the sequence allows for the possibility of a concealed representation within a different number system.
4. Recursive Relationships:
A recursive relationship defines each term in the sequence based on previous terms. Let's explore possible recursive patterns:
- It's difficult to establish a simple recursive relationship directly from the sequence 1 1 4 2 3. More data points would be beneficial for identifying a potentially recursive pattern. To illustrate a recursive concept, let's consider a different, simpler example: The Fibonacci sequence (1, 1, 2, 3, 5...) where each term is the sum of the two preceding terms. In our case, finding a recursive relationship requires either additional terms or a different approach entirely.
5. Considering External Factors and Context:
The meaning of "1 1 4 2 3" might be entirely dependent on its context. Is this a fragment of a larger sequence? Could it represent a code, a cipher, or coordinates in a system not readily apparent? The sequence, without further information, remains open to diverse interpretations. This underscores the importance of context when analyzing numerical sequences or any type of code.
Expanding the Possibilities: The Role of Additional Data
Without additional information or terms in the sequence, establishing a definitive rule or pattern remains challenging. If we were provided with more numbers following "1 1 4 2 3," the possibilities for identifying a pattern would significantly increase. For instance, consider these potential extensions:
-
Extension 1: 1 1 4 2 3 5 8...: This resembles the Fibonacci sequence, starting from the third term.
-
Extension 2: 1 1 4 2 3 1 1...: This suggests a repeating or cyclical pattern.
-
Extension 3: 1 1 4 2 3 6 7...: This could hint towards a sequence involving prime numbers or other number properties.
The provision of additional terms would allow for a more rigorous analysis, leading to a stronger conclusion regarding the sequence's underlying rule or structure.
The Importance of Mathematical Reasoning and Problem-Solving
The exercise of deciphering "1 1 4 2 3" demonstrates the importance of multiple approaches in problem-solving. We've explored difference analysis, prime numbers, number bases, and recursion, all without arriving at a single, definitive answer. This highlights the importance of flexible thinking and the iterative nature of mathematical exploration. Often, the path to a solution involves testing several hypotheses and refining our approach based on the results.
Conclusion: Embracing Ambiguity in Mathematics
The sequence "1 1 4 2 3" serves as a compelling reminder that not all mathematical problems have a singular, readily apparent solution. The beauty of mathematics lies in its capacity to encompass multiple perspectives and interpretations. The ambiguity presented by this sequence encourages creativity, critical thinking, and the exploration of various mathematical tools and techniques. While we haven't uncovered a single conclusive pattern, the journey of exploration itself offers valuable insights into the world of pattern recognition and mathematical reasoning. The lack of a definitive answer emphasizes the importance of continued investigation and open-mindedness when approaching challenging mathematical puzzles. Ultimately, the value lies not just in finding the "right" answer, but in the process of discovery and the development of analytical skills along the way.
Frequently Asked Questions (FAQ)
-
Q: Is there one correct answer to this sequence? A: Without further information or context, there is no single "correct" answer. Multiple interpretations are possible, each valid within its own framework.
-
Q: Why is this sequence so difficult to solve? A: The brevity of the sequence and the lack of an immediately apparent pattern contribute to its difficulty. More data points would provide stronger evidence for a particular pattern.
-
Q: What skills are required to solve a puzzle like this? A: Problem-solving skills such as pattern recognition, logical reasoning, creativity, and the ability to explore multiple approaches are crucial. A strong understanding of number theory is also beneficial.
-
Q: How can I improve my ability to solve similar sequences? A: Practice is key! Work through various numerical sequence puzzles, exploring different methods and approaches. Familiarize yourself with different number properties and mathematical concepts.
This exploration of "1 1 4 2 3" showcases the fascinating interplay between observation, logic, and mathematical principles. Even seemingly simple numerical sequences can lead to intricate explorations and reveal the diverse facets of mathematical thinking. The journey of discovery, rather than the arrival at a definitive answer, constitutes the true essence of mathematical problem-solving.
Latest Posts
Latest Posts
-
Gcf Of 100 And 30
Sep 14, 2025
-
What Time Is 17 39
Sep 14, 2025
-
Gcf Of 8 And 4
Sep 14, 2025
-
Gcf Of 56 And 64
Sep 14, 2025
-
3 6 As A Mixed Number
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.