Gcf Of 8 And 4
saludintensiva
Sep 14, 2025 · 7 min read
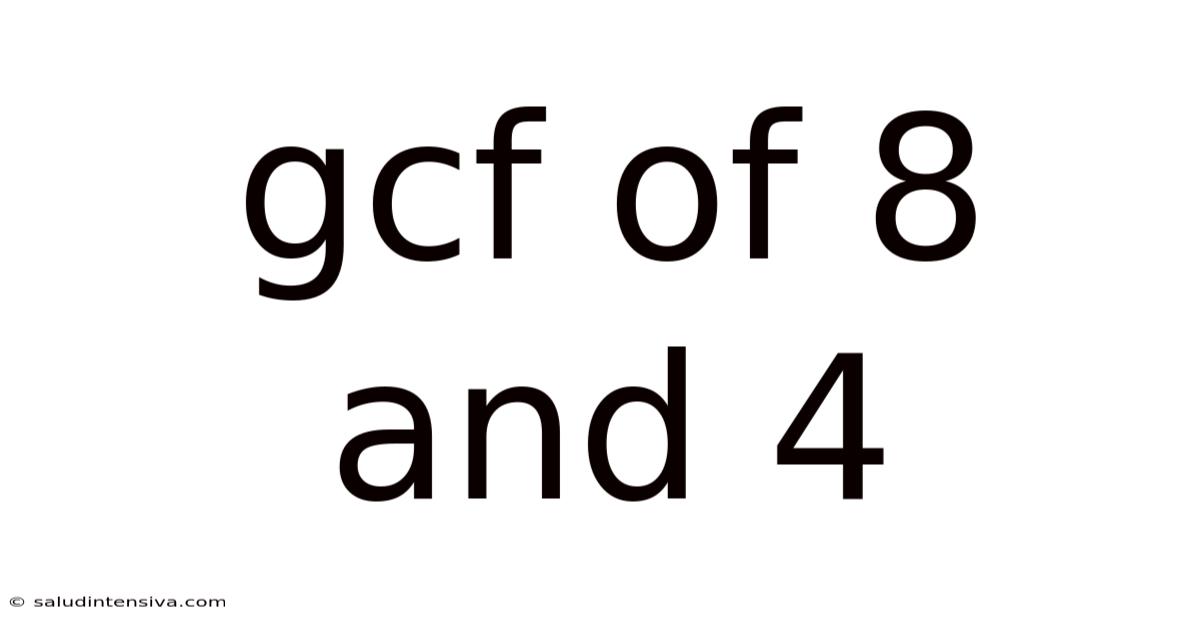
Table of Contents
Understanding the Greatest Common Factor (GCF): A Deep Dive into the GCF of 8 and 4
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, especially when dealing with small numbers like 8 and 4. However, understanding the underlying concepts and various methods for calculating the GCF is crucial for building a strong foundation in mathematics. This article will provide a comprehensive exploration of the GCF, focusing on the GCF of 8 and 4, while also expanding upon the broader applications and significance of this fundamental concept. We will delve into different methods, explain the underlying principles, and address frequently asked questions, ensuring a thorough understanding for learners of all levels. This will equip you not only to solve problems involving 8 and 4, but also to tackle more complex GCF calculations confidently.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's essentially the largest shared factor among a set of numbers. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6. This concept is fundamental in various mathematical applications, from simplifying fractions to solving algebraic equations.
Finding the GCF is a crucial skill in simplifying fractions. For example, simplifying the fraction 12/18 requires finding the GCF of 12 and 18, which is 6. Dividing both the numerator and denominator by 6 gives us the simplified fraction 2/3. This simplification makes calculations easier and provides a more concise representation of the fraction.
Finding the GCF of 8 and 4: Methods and Explanation
Let's now focus on finding the GCF of 8 and 4. Several methods can be employed, each offering a unique approach to solving the problem. We will explore the most common techniques:
1. Listing Factors Method
This is a straightforward approach, especially suitable for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
- Factors of 8: 1, 2, 4, 8
- Factors of 4: 1, 2, 4
Comparing the two lists, we see that the common factors are 1, 2, and 4. The greatest among these is 4. Therefore, the GCF of 8 and 4 is 4.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 4: 2 x 2 = 2²
The only common prime factor is 2. The lowest power of 2 present in both factorizations is 2². Therefore, the GCF of 8 and 4 is 2² = 4.
3. Euclidean Algorithm
This method is particularly useful for larger numbers. It involves a series of divisions until the remainder is 0. The last non-zero remainder is the GCF.
- Divide the larger number (8) by the smaller number (4): 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the divisor in the last step, which is 4.
The Euclidean algorithm provides a systematic and efficient approach, especially when dealing with larger numbers where listing factors or prime factorization might become cumbersome.
GCF in Real-World Applications
The GCF isn't just a theoretical concept; it finds practical applications in various real-world scenarios:
-
Simplifying Fractions: As mentioned earlier, the GCF is crucial for simplifying fractions to their lowest terms. This simplifies calculations and makes fractions easier to understand and compare.
-
Dividing Objects Equally: Imagine you have 8 apples and 4 oranges, and you want to divide them into equal groups. The GCF (4) indicates you can create 4 equal groups, each containing 2 apples and 1 orange.
-
Geometry and Measurement: The GCF plays a vital role in solving problems related to area, perimeter, and volume. For instance, if you need to tile a rectangular floor with square tiles, the GCF of the floor's dimensions determines the largest size of square tiles that can be used without cutting any tiles.
-
Music and Rhythm: In music theory, the GCF is used to determine the greatest common divisor of two or more note values, which helps in understanding rhythmic relationships and simplifying complex musical notation.
-
Computer Science: The concept of GCF is utilized in various algorithms and data structures, such as finding the least common multiple (LCM) which is closely related to the GCF, used extensively in scheduling and resource management within computer systems.
Expanding the Concept: GCF of More Than Two Numbers
The principles of finding the GCF extend to situations involving more than two numbers. Let's consider finding the GCF of 12, 18, and 24. We can apply the prime factorization method:
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
- Prime factorization of 24: 2³ x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF of 12, 18, and 24 is 2 x 3 = 6.
The Relationship Between GCF and LCM
The greatest common factor (GCF) and the least common multiple (LCM) are closely related concepts. The LCM is the smallest number that is a multiple of two or more given numbers. For any two numbers a and b, the product of their GCF and LCM is equal to the product of the two numbers themselves:
GCF(a, b) x LCM(a, b) = a x b
For example, with the numbers 8 and 4:
GCF(8, 4) = 4 LCM(8, 4) = 8
4 x 8 = 32 8 x 4 = 32
This relationship provides a useful shortcut for calculating the LCM if the GCF is known, or vice versa.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This signifies that they share no common factors other than 1. For example, the GCF of 9 and 10 is 1.
Q2: Can the GCF of two numbers be larger than the smaller number?
A2: No, the GCF of two numbers can never be larger than the smaller of the two numbers. The GCF is, by definition, a factor of both numbers, and a factor cannot be greater than the number itself.
Q3: Are there any limitations to the Euclidean algorithm?
A3: While the Euclidean algorithm is efficient for finding the GCF of two numbers, it can become computationally intensive for very large numbers. More advanced algorithms are used in such cases for optimized performance.
Q4: How do I find the GCF of three or more numbers efficiently?
A4: For multiple numbers, the prime factorization method or repeated application of the Euclidean algorithm (finding the GCF of two numbers at a time and then repeating the process with the result and the next number) are generally efficient approaches.
Conclusion
Understanding the greatest common factor (GCF) is fundamental to a strong grasp of mathematics. We've explored various methods for calculating the GCF, particularly focusing on the GCF of 8 and 4, which is 4. We've seen how this seemingly simple concept has practical applications across various fields, from simplifying fractions to solving real-world problems involving division and measurement. Beyond the basic calculations, we’ve also delved into the relationship between GCF and LCM and discussed approaches for finding the GCF of multiple numbers. By mastering the concepts and techniques presented here, you'll be well-equipped to tackle more complex mathematical problems with confidence and understanding. Remember that consistent practice and a deep understanding of the underlying principles are key to mastering any mathematical concept, and the GCF is no exception.
Latest Posts
Latest Posts
-
3 2 In Simplest Form
Sep 15, 2025
-
0 34 Acres To Sq Ft
Sep 15, 2025
-
Whats 8 As A Fraction
Sep 15, 2025
-
3 To The 6 Power
Sep 15, 2025
-
What Is 6 9 Reduced
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 8 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.