3 2 In Simplest Form
saludintensiva
Sep 15, 2025 · 6 min read
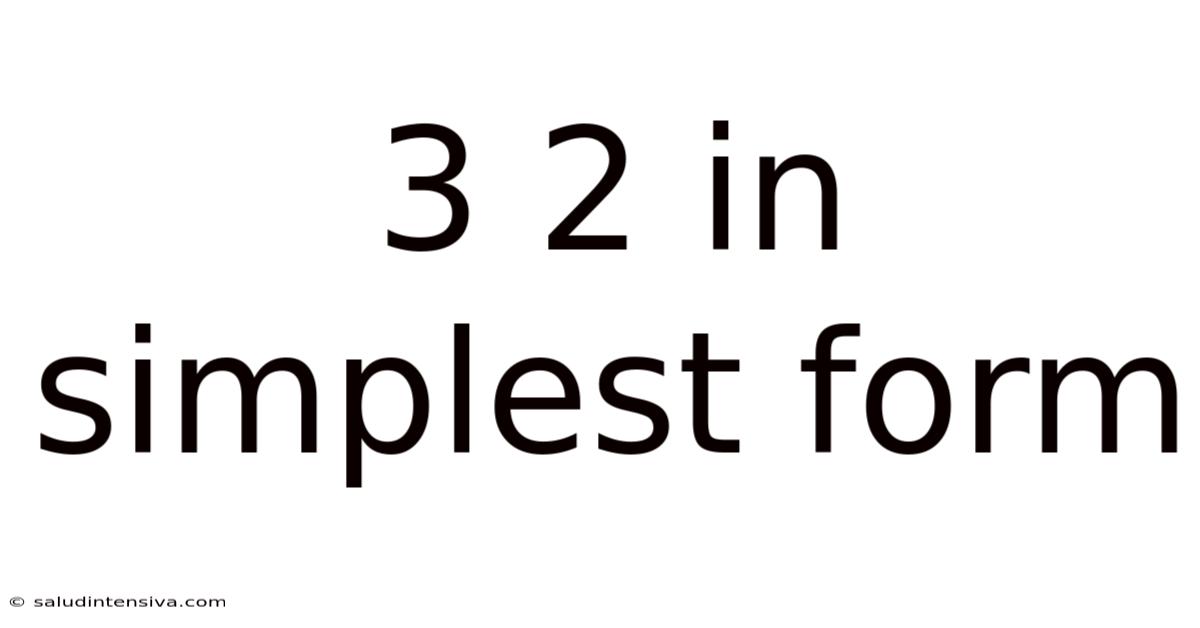
Table of Contents
Understanding Fractions: Simplifying 3/2 to its Simplest Form
Fractions are a fundamental concept in mathematics, representing parts of a whole. Understanding how to simplify fractions is crucial for various mathematical operations and real-world applications. This article will delve into the simplification of the fraction 3/2, exploring the process, the underlying mathematical principles, and common misconceptions. We will also address frequently asked questions and provide practical examples to solidify your understanding. Learning to simplify fractions like 3/2 will build a strong foundation for more advanced mathematical concepts.
What is a Fraction?
Before diving into the simplification of 3/2, let's briefly revisit the concept of a fraction. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For example, in the fraction 3/2, 3 is the numerator and 2 is the denominator. This means we have 3 parts out of a whole that's divided into 2 parts.
Simplifying Fractions: The Basics
Simplifying a fraction means reducing it to its lowest terms, meaning there is no common factor (other than 1) between the numerator and the denominator. This process involves finding the greatest common divisor (GCD) or greatest common factor (GCF) of both numbers and dividing both the numerator and the denominator by that GCD. This doesn't change the value of the fraction; it simply expresses it in a more concise and manageable form.
Simplifying 3/2: A Step-by-Step Guide
The fraction 3/2 is an improper fraction because the numerator (3) is larger than the denominator (2). Improper fractions often represent values greater than 1. Simplifying 3/2 doesn't involve finding a common factor and reducing, but rather converting it to a mixed number or an equivalent decimal.
Step 1: Identify the type of fraction. 3/2 is an improper fraction.
Step 2: Convert to a mixed number. To convert an improper fraction to a mixed number, we perform division. Divide the numerator (3) by the denominator (2):
3 ÷ 2 = 1 with a remainder of 1.
The quotient (1) becomes the whole number part of the mixed number. The remainder (1) becomes the numerator of the fractional part, and the denominator remains the same (2). Therefore, 3/2 as a mixed number is 1 1/2.
Step 3: (Optional) Convert to a decimal. To express 3/2 as a decimal, simply perform the division:
3 ÷ 2 = 1.5
Therefore, 3/2 is equal to 1.5.
Mathematical Explanation: Why Simplification Works
The process of simplifying fractions relies on the fundamental principle of equivalent fractions. Equivalent fractions represent the same value even though they have different numerators and denominators. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half.
When we simplify a fraction by dividing both the numerator and denominator by their GCD, we are essentially creating an equivalent fraction with smaller numbers. This doesn't change the fundamental ratio; it just expresses it in a more concise form.
Common Misconceptions about Fraction Simplification
-
Incorrectly canceling terms: A common mistake is to incorrectly cancel terms that are not common factors. For instance, in a fraction like 15/25, students might incorrectly cancel the 5 in the numerator and denominator separately, resulting in 1/1. The correct way is to find the GCD (which is 5) and divide both the numerator and denominator by 5, resulting in 3/5.
-
Forgetting about negative signs: When dealing with negative fractions, remember that the negative sign can apply to either the numerator, the denominator, or the entire fraction. Ensure you correctly handle the sign during simplification.
-
Not simplifying completely: Always double-check to ensure you've divided by the greatest common divisor. If you don't, you'll need to simplify again.
Practical Applications of Fraction Simplification
Simplifying fractions is not just an academic exercise. It has numerous practical applications in various fields, including:
-
Cooking and Baking: Following recipes often involves working with fractions of ingredients. Simplifying fractions helps to understand the proportions more clearly.
-
Construction and Engineering: Calculations in construction and engineering frequently involve fractions. Simplified fractions ensure accuracy and ease of calculation.
-
Finance and Accounting: Dealing with percentages and proportions in financial calculations often requires simplifying fractions.
-
Everyday Life: Many everyday tasks, such as sharing items fairly or measuring ingredients, involve fractions.
Frequently Asked Questions (FAQ)
Q: Is 3/2 in its simplest form?
A: No, 3/2 is an improper fraction. While it's not simplified in the traditional sense (as there's no common factor to divide by), it can be simplified into a mixed number (1 1/2) or a decimal (1.5). The “simplest form” depends on the context and desired representation.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes calculations easier and results more understandable. It helps in comparing fractions, performing arithmetic operations (addition, subtraction, multiplication, and division), and understanding proportions more effectively.
Q: How do I find the greatest common divisor (GCD)?
A: There are several methods for finding the GCD, including:
-
Listing factors: List all factors of both the numerator and denominator and find the largest one they have in common.
-
Prime factorization: Express both numbers as products of their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
-
Euclidean algorithm: A more efficient algorithm for finding the GCD, particularly for larger numbers.
Q: Can I simplify a fraction by multiplying the numerator and denominator by the same number?
A: No, multiplying the numerator and denominator by the same number creates an equivalent fraction, not a simplified one. Simplifying involves dividing by a common factor.
Conclusion
Simplifying fractions is a fundamental skill in mathematics with wide-ranging applications. While the fraction 3/2 doesn't simplify in the traditional sense of reducing an improper fraction to a proper one by finding a common factor, converting it to a mixed number (1 1/2) or decimal (1.5) provides a more easily understandable and usable form. Mastering the concept of fraction simplification, including understanding equivalent fractions and finding the GCD, is crucial for building a solid mathematical foundation and successfully tackling more complex problems. Remember to practice regularly and pay close attention to detail to avoid common mistakes. By understanding the underlying principles and practicing consistently, you can confidently simplify fractions and apply this knowledge in various real-world scenarios.
Latest Posts
Latest Posts
-
Lcm Of 16 And 14
Sep 15, 2025
-
Gcf Of 34 And 85
Sep 15, 2025
-
11 18 As A Decimal
Sep 15, 2025
-
3 5 8 As A Decimal
Sep 15, 2025
-
13 12 As A Percent
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 2 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.