Gcf Of 34 And 85
saludintensiva
Sep 15, 2025 · 5 min read
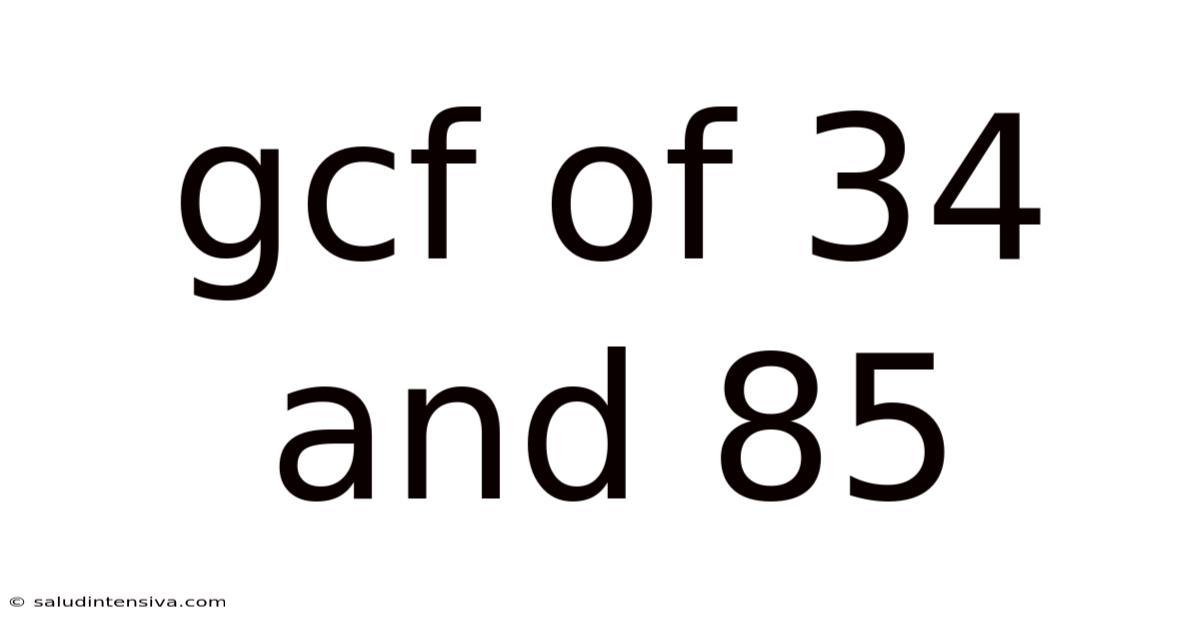
Table of Contents
Finding the Greatest Common Factor (GCF) of 34 and 85: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve into the process of determining the GCF of 34 and 85, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll move beyond simply finding the answer and examine the broader implications and applications of this mathematical concept. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and even tackling more advanced mathematical problems.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Then, we identify the common prime factors and multiply them together to find the GCF.
Let's apply this to find the GCF of 34 and 85:
1. Prime Factorization of 34:
34 can be factored as 2 x 17. Both 2 and 17 are prime numbers.
2. Prime Factorization of 85:
85 can be factored as 5 x 17. Both 5 and 17 are prime numbers.
3. Identifying Common Prime Factors:
Both 34 and 85 share the prime factor 17.
4. Calculating the GCF:
Since 17 is the only common prime factor, the GCF of 34 and 85 is $\boxed{17}$.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both lists.
1. Factors of 34:
The factors of 34 are 1, 2, 17, and 34.
2. Factors of 85:
The factors of 85 are 1, 5, 17, and 85.
3. Identifying Common Factors:
The common factors of 34 and 85 are 1 and 17.
4. Determining the GCF:
The largest common factor is 17, therefore, the GCF of 34 and 85 is $\boxed{17}$.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 34 and 85:
-
Start with the larger number (85) and the smaller number (34).
-
Divide the larger number by the smaller number and find the remainder:
85 ÷ 34 = 2 with a remainder of 17.
-
Replace the larger number with the smaller number (34) and the smaller number with the remainder (17).
-
Repeat the division:
34 ÷ 17 = 2 with a remainder of 0.
-
Since the remainder is 0, the GCF is the last non-zero remainder, which is $\boxed{17}$.
Why is finding the GCF important?
The concept of the GCF has wide-ranging applications across various mathematical fields and real-world scenarios. Here are a few examples:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and denominator by their GCF. For example, the fraction 34/85 can be simplified to 2/5 by dividing both the numerator and denominator by their GCF, which is 17.
-
Solving Algebraic Equations: Finding the GCF is often a necessary step in solving algebraic equations, particularly those involving factoring polynomials.
-
Geometry and Measurement: GCF is used in problems involving finding the largest possible square tiles to cover a rectangular floor or determining the largest common measurement of two lengths.
-
Number Theory: The GCF is a fundamental concept in number theory, used in various theorems and proofs.
-
Computer Science: The Euclidean algorithm, a method for finding the GCF, is used in cryptography and other areas of computer science.
Frequently Asked Questions (FAQ)
-
What if the GCF of two numbers is 1? If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they have no common factors other than 1.
-
Can the GCF of two numbers be greater than the smaller number? No, the GCF of two numbers can never be greater than the smaller of the two numbers.
-
Is there a formula to find the GCF? There isn't a single formula for finding the GCF, but the methods described above (prime factorization, listing factors, and the Euclidean algorithm) provide systematic approaches.
-
Which method is the best for finding the GCF? The best method depends on the numbers involved. For small numbers, listing factors might be quickest. For larger numbers, the Euclidean algorithm is generally more efficient. Prime factorization is a useful method for understanding the underlying structure of the numbers.
Conclusion
Finding the greatest common factor (GCF) of 34 and 85, as demonstrated through prime factorization, listing factors, and the Euclidean algorithm, consistently yields the result of 17. Understanding the GCF is not just about solving a specific problem; it's about grasping a fundamental mathematical concept that underpins various areas of mathematics and has practical applications in numerous fields. By mastering these methods, you gain a powerful tool for simplifying problems, solving equations, and deepening your understanding of numbers and their relationships. Remember to choose the method that best suits the numbers you are working with, and practice regularly to solidify your understanding. The more you work with GCF, the more intuitive and efficient you'll become at finding it.
Latest Posts
Latest Posts
-
Converting Decimals Into Mixed Numbers
Sep 15, 2025
-
5 Divided By 1 4
Sep 15, 2025
-
150kg Is How Many Pounds
Sep 15, 2025
-
30 Days From 10 3
Sep 15, 2025
-
Lump Sum Present Value Formula
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 34 And 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.