5 Divided By 1 4
saludintensiva
Sep 15, 2025 · 5 min read
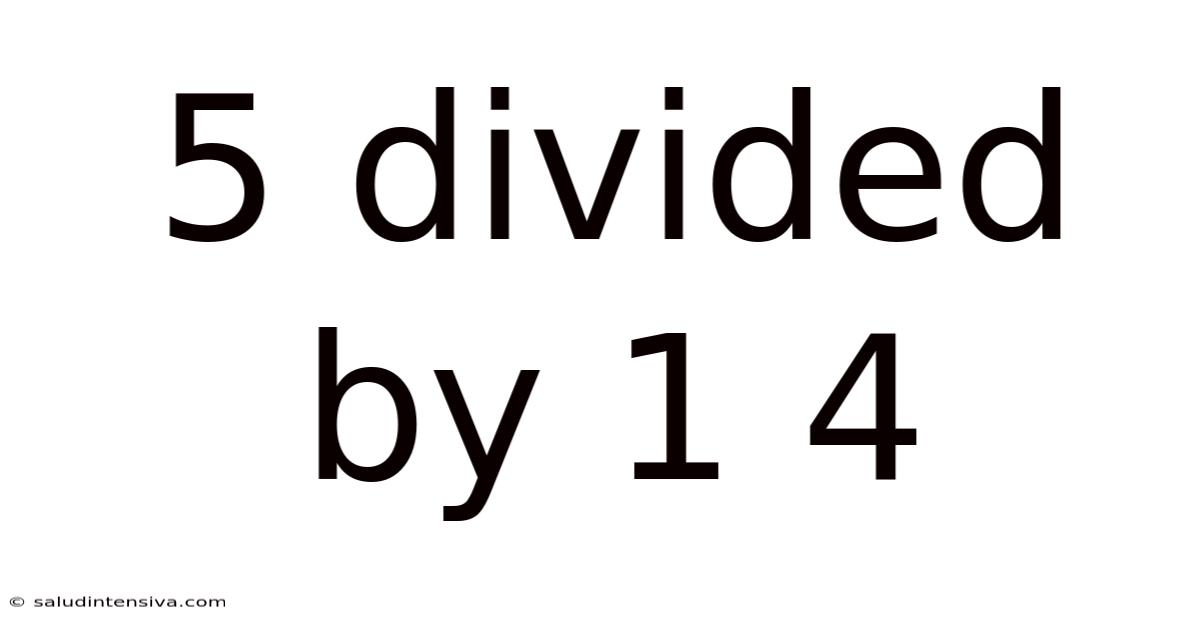
Table of Contents
Understanding 5 Divided by 1 ¼: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a systematic approach, it becomes surprisingly straightforward. This article will thoroughly explore the process of dividing 5 by 1 ¼, explaining the steps involved, the underlying mathematical principles, and offering practical applications to solidify your understanding. This will cover everything from basic fraction manipulation to real-world examples, ensuring a comprehensive understanding of this seemingly simple yet insightful mathematical operation.
Introduction: Deconstructing the Problem
The problem, 5 ÷ 1 ¼, presents a common challenge in arithmetic: dividing a whole number by a mixed fraction. While it might look intimidating at first glance, breaking it down into smaller, manageable steps reveals a clear and logical solution. This process involves converting the mixed fraction into an improper fraction, then applying the reciprocal method of fraction division. We'll delve into each step in detail, clarifying any potential points of confusion. The core concept revolves around understanding the relationship between division and multiplication, a fundamental aspect of arithmetic that underpins many more complex mathematical concepts.
Step-by-Step Solution: From Mixed Fraction to Final Answer
-
Convert the Mixed Fraction to an Improper Fraction: The first crucial step is transforming the mixed fraction 1 ¼ into an improper fraction. A mixed fraction combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). To convert it, we multiply the whole number (1) by the denominator (4), add the numerator (1), and place the result over the original denominator:
(1 x 4) + 1 = 5
Therefore, 1 ¼ becomes 5/4.
-
Rewrite the Division as Multiplication: Division by a fraction is equivalent to multiplication by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. So, dividing by 5/4 is the same as multiplying by 4/5. Our problem now becomes:
5 ÷ 5/4 = 5 x 4/5
-
Perform the Multiplication: Now, we multiply the whole number (5) by the numerator of the fraction (4), and place the result over the denominator (5):
5 x 4 = 20
So we have 20/5.
-
Simplify the Result: Finally, we simplify the resulting improper fraction. 20 divided by 5 equals 4.
Therefore, 5 ÷ 1 ¼ = 4
Visualizing the Division: A Geometric Approach
To further enhance understanding, let's visualize this division problem geometrically. Imagine you have 5 identical squares representing the whole number 5. Now, imagine each square is divided into four equal parts. This represents dividing each whole unit into fourths. The question then becomes: how many sets of 1 ¼ (which is 5 fourths) can you make from these 20 fourths? Clearly, you can make 4 such sets. This visual representation confirms our calculated answer of 4.
The Mathematical Rationale: Exploring Reciprocals and Inverse Operations
The method we used relies on the fundamental relationship between division and multiplication. Division is the inverse operation of multiplication. When we divide a number by a fraction, we're essentially asking: "How many times does this fraction fit into the number?" Multiplying by the reciprocal effectively answers this question. The reciprocal, also known as the multiplicative inverse, is a number that, when multiplied by the original number, yields 1. This principle extends beyond fractions to all numbers except zero (you cannot have a reciprocal of zero).
Extending the Concept: Dividing Other Whole Numbers by Mixed Fractions
The method demonstrated above can be applied to any problem involving dividing a whole number by a mixed fraction. Let's consider another example: 7 ÷ 2 ½.
-
Convert 2 ½ to an improper fraction: (2 x 2) + 1 = 5/2
-
Rewrite the division as multiplication: 7 ÷ 5/2 = 7 x 2/5
-
Perform the multiplication: 7 x 2 = 14
-
Simplify the result: 14/5 = 2 and 4/5
This demonstrates the adaptability and generalizability of the method. The core principle remains consistent regardless of the specific numbers involved.
Real-World Applications: Putting Fraction Division into Practice
Fraction division is not just an abstract mathematical concept; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require dividing ingredients. If a recipe calls for 2 ½ cups of flour, and you want to make half the recipe, you need to divide 2 ½ by 2.
-
Construction and Measurement: Dividing lengths and quantities is crucial in many construction and engineering projects. For example, calculating how many 1 ¼ foot-long boards are needed to cover a 5-foot length.
-
Finance and Budgeting: Dividing a budget among different categories often requires dealing with fractions.
-
Sewing and Crafting: Calculating fabric needs often involves dividing lengths and widths.
-
Data Analysis: In data analysis, dividing quantities can be necessary to calculate averages or proportions.
These are just a few examples illustrating the widespread practical use of fraction division. Mastering this concept provides a strong foundation for tackling more complex mathematical problems in various fields.
Frequently Asked Questions (FAQ)
-
Q: What if I have a negative mixed fraction?
- A: Treat the negative sign separately. Convert the mixed fraction to an improper fraction, perform the multiplication, and then apply the negative sign to the final answer.
-
Q: Can I use a calculator to solve these problems?
- A: Yes, calculators can be used to verify answers or handle more complex calculations. However, understanding the underlying principles is crucial for developing a strong mathematical foundation.
-
Q: What if I have two mixed fractions involved in a division problem?
- A: Convert both mixed fractions to improper fractions, then apply the reciprocal method for fraction division as described above.
Conclusion: Mastering Fraction Division for a Stronger Mathematical Foundation
Understanding how to divide whole numbers by mixed fractions is a fundamental skill that builds a solid foundation for more advanced mathematical concepts. While initially appearing challenging, the process is straightforward once you grasp the steps involved: converting mixed fractions to improper fractions, applying the reciprocal rule for division, and simplifying the result. This approach is not merely a set of procedures but a reflection of the fundamental inverse relationship between multiplication and division, a key element in arithmetic and algebra. By mastering this process, you not only solve specific problems but also deepen your understanding of fundamental mathematical operations, paving the way for further exploration and success in higher-level mathematics and its diverse real-world applications. Remember to practice regularly to reinforce your understanding and build confidence in tackling more complex fraction problems.
Latest Posts
Latest Posts
-
How Long Is 4 Meters
Sep 15, 2025
-
81 F To Degree Celsius
Sep 15, 2025
-
Gcf Of 7 And 21
Sep 15, 2025
-
5 To Power Of 4
Sep 15, 2025
-
Lcm Of 30 And 42
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.