1 1 4 3 8
saludintensiva
Sep 12, 2025 · 6 min read
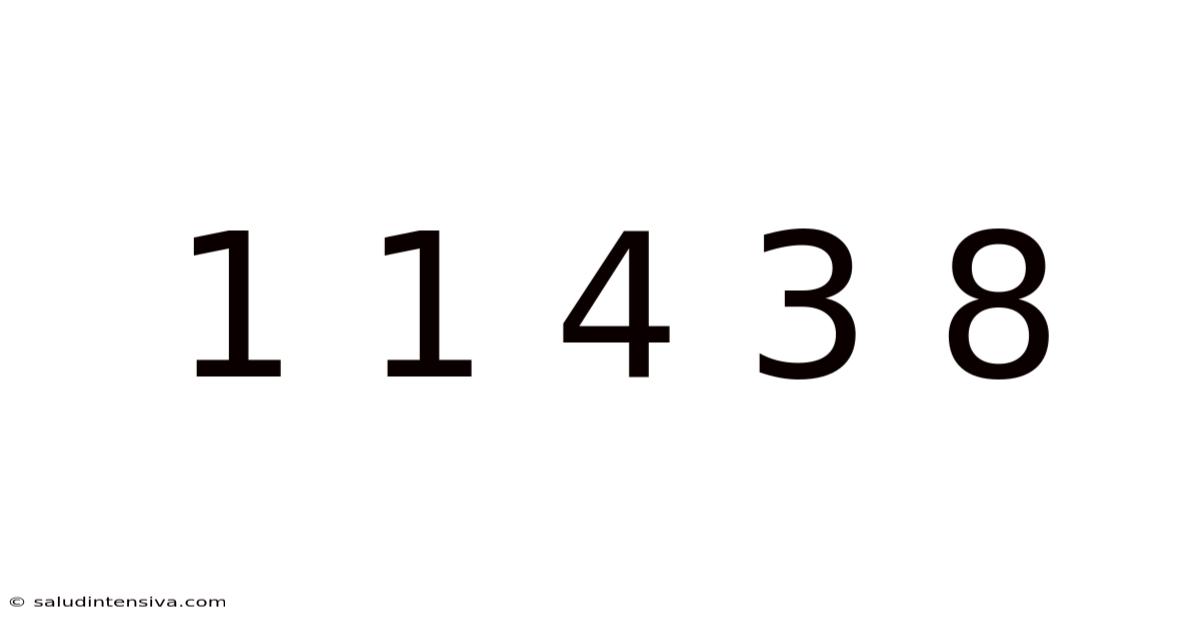
Table of Contents
Unlocking the Mystery: The Curious Sequence 1 1 4 3 8
The seemingly simple sequence 1, 1, 4, 3, 8… might appear innocuous at first glance. However, beneath its unassuming exterior lies a fascinating exploration of mathematical patterns, logical deduction, and the creative process of finding solutions. This article delves deep into this numerical puzzle, exploring potential patterns, offering different approaches to understanding the sequence, and ultimately demonstrating how seemingly simple problems can lead to complex and rewarding intellectual pursuits. We will investigate multiple possibilities and highlight the importance of considering diverse perspectives when tackling mathematical problems.
Potential Interpretations and Patterns
The initial challenge with the sequence 1, 1, 4, 3, 8 is its ambiguity. Unlike sequences with readily apparent arithmetic or geometric progressions, this one requires more creative thinking. There isn't one single "correct" answer; instead, multiple plausible patterns can be identified, each requiring a unique line of reasoning. This ambiguity highlights the richness of mathematical exploration and the importance of considering multiple perspectives.
Approach 1: Operations Between Consecutive Numbers
One approach involves examining the relationships between consecutive numbers. Let's analyze the differences:
- 1 - 1 = 0
- 4 - 1 = 3
- 3 - 4 = -1
- 8 - 3 = 5
This doesn't immediately reveal a consistent pattern. However, let's look at the differences between these differences:
- 3 - 0 = 3
- -1 - 3 = -4
- 5 - (-1) = 6
Again, no readily apparent pattern emerges. This method doesn't seem to yield a clear solution, but it demonstrates a valuable problem-solving strategy: systematically examining differences to uncover underlying relationships.
Approach 2: Exploring Quadratic Relationships
Another approach involves considering if the sequence could be represented by a quadratic equation of the form an² + bn + c, where 'n' represents the position of the number in the sequence (1, 2, 3, 4, 5...). We can set up a system of equations:
- For n=1: a(1)² + b(1) + c = 1
- For n=2: a(2)² + b(2) + c = 1
- For n=3: a(3)² + b(3) + c = 4
- For n=4: a(4)² + b(4) + c = 3
- For n=5: a(5)² + b(5) + c = 8
Solving this system of equations would require matrix methods or other advanced algebraic techniques. While this approach might yield a quadratic equation that fits the first five terms, there's no guarantee it will accurately predict subsequent terms. This highlights the limitations of solely relying on curve fitting without a deeper understanding of the underlying pattern's origin.
Approach 3: Building a Recursive Relationship
A recursive sequence defines each term based on preceding terms. This approach might involve exploring formulas that use the previous one or two terms to generate the next. For instance, we could speculate:
- a(n) = a(n-1) + f(a(n-2), a(n-1))
Where 'f' is some function of the previous two terms. Finding the appropriate 'f' would require considerable experimentation and might lead to several potential solutions. The challenge lies in identifying a function that consistently produces the observed sequence and can be extrapolated to predict future terms. This demonstrates the iterative nature of mathematical problem-solving; testing different functions and refining our approach until a satisfactory solution (or at least a plausible hypothesis) is found.
Approach 4: Prime Numbers and Their Properties
A more abstract approach might consider connections to prime numbers or other number-theoretic concepts. While 1 isn't technically a prime number, and 4 and 8 are not prime, we might explore if there's a relationship between the sequence and the factorization or properties of numbers near these values. For example, we might examine the prime factorization of numbers close to each element in the sequence. This demonstrates how diverse mathematical concepts can be applied to the same problem, leading to potentially insightful observations.
The Importance of Context and Further Information
The inherent difficulty in definitively solving the 1, 1, 4, 3, 8 sequence lies in the lack of context. Without additional information about the sequence's origin or the rules governing its generation, multiple solutions are possible. This underscores the significance of context in problem-solving. If the sequence were part of a larger problem – perhaps a coding challenge, a physics equation, or a game – additional clues might narrow down the possibilities and reveal the intended pattern.
Expanding the Sequence: Predictive Modeling
Even without a definitive solution, we can explore predictive modeling. Let's assume, for example, that a recursive relationship, albeit an unknown one, governs the sequence. We might then use various statistical methods like time series analysis or machine learning algorithms to attempt predicting future terms. This predictive approach acknowledges the inherent uncertainty while still allowing us to explore potential future values within the sequence.
This would involve training a model on the existing five data points and then using it to predict the sixth, seventh, and subsequent terms. However, it's crucial to remember that the accuracy of such predictions strongly depends on the underlying pattern and the model's ability to capture it accurately. The model could be inaccurate if the underlying pattern is complex or if there is noise within the data, leading to overfitting.
The Value of Mathematical Exploration
The 1, 1, 4, 3, 8 sequence, though seemingly simple, provides a valuable lesson in mathematical exploration. It demonstrates that:
- Multiple solutions are possible: The lack of a single "correct" answer emphasizes the richness and diversity of mathematical reasoning.
- Systematic approaches are crucial: Organized methods like examining differences, exploring quadratic equations, and considering recursive relationships are vital problem-solving tools.
- Context matters: Additional information can drastically change our understanding and interpretation of a given problem.
- Creativity and intuition are valuable: Sometimes, unconventional thinking and exploration of seemingly unrelated concepts lead to unexpected insights.
- Predictive modeling is a powerful tool: Even with incomplete information, we can use various statistical and machine learning methods to predict future values and investigate trends.
This exercise in investigating the sequence serves as a reminder that the journey of mathematical exploration is often more rewarding than reaching a specific destination. The process of investigating different approaches, testing hypotheses, and grappling with ambiguity fosters critical thinking, creative problem-solving, and a deeper appreciation for the beauty and complexity of mathematics. Therefore, rather than seeking one definitive answer, we should appreciate the numerous pathways to understanding the sequence and the valuable lessons learned along the way.
Conclusion
The seemingly simple sequence 1, 1, 4, 3, 8 encapsulates the essence of mathematical exploration. It showcases the importance of multiple perspectives, systematic analysis, and creative thinking in uncovering underlying patterns. While a definitive solution remains elusive without further context, the various approaches explored highlight the power of mathematical reasoning and problem-solving techniques. The experience of grappling with this numerical puzzle provides a valuable lesson in embracing ambiguity, exploring multiple avenues, and ultimately appreciating the richness of mathematical inquiry. The journey of exploration itself is often more insightful than arriving at a singular solution.
Latest Posts
Latest Posts
-
7 10 As A Percent
Sep 12, 2025
-
Gcf Of 72 And 36
Sep 12, 2025
-
17 50 As A Decimal
Sep 12, 2025
-
Gcf Of 18 And 15
Sep 12, 2025
-
Is 4 10 Less Than 1 2
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.