Gcf Of 18 And 15
saludintensiva
Sep 12, 2025 · 6 min read
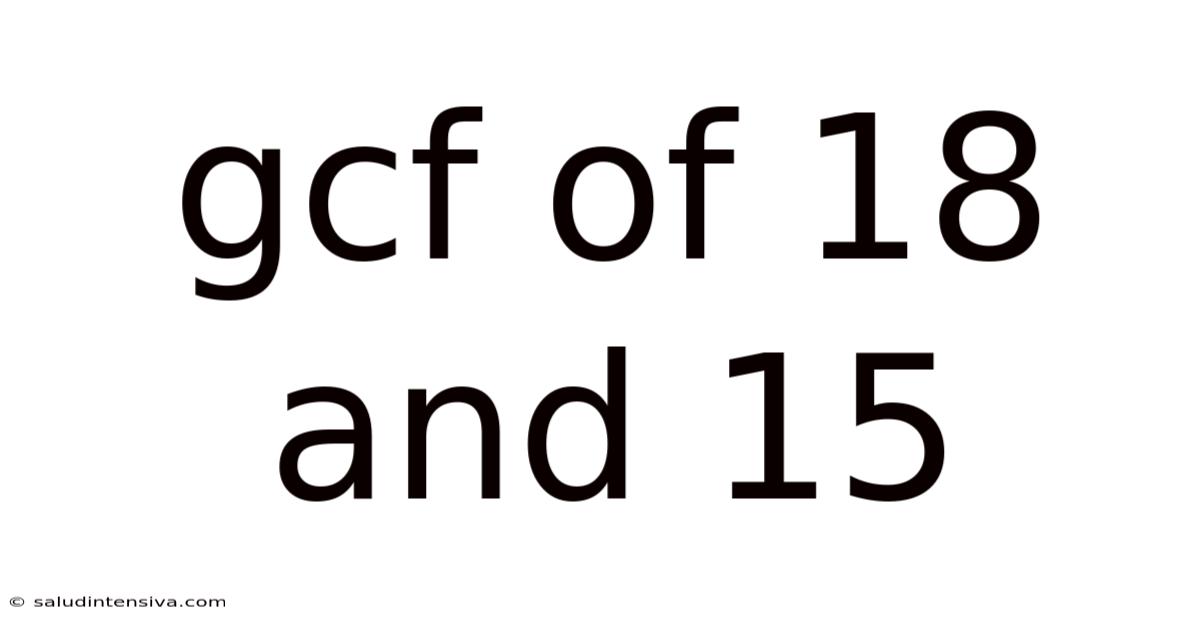
Table of Contents
Finding the Greatest Common Factor (GCF) of 18 and 15: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This guide will walk you through several methods to determine the GCF of 18 and 15, explaining the underlying principles and providing a deeper understanding of this important mathematical operation. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical problems. This article will equip you with the knowledge and skills to confidently find the GCF of any two numbers.
Understanding Greatest Common Factor (GCF)
Before diving into the calculation, let's clarify what the GCF actually is. The greatest common factor of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 18 and 15. Let's list all the factors of each number:
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 15: 1, 3, 5, 15
Now, let's identify the common factors: 1 and 3.
The greatest of these common factors is 3. Therefore, the GCF of 18 and 15 is 3.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Prime factorization of 18:
18 = 2 x 9 = 2 x 3 x 3 = 2 x 3²
Prime factorization of 15:
15 = 3 x 5
Now, we identify the common prime factors. Both 18 and 15 share only one prime factor: 3. To find the GCF, we multiply the common prime factors together. In this case, the GCF is simply 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially useful for larger numbers where listing factors becomes cumbersome. This algorithm relies on repeated division.
The steps are as follows:
-
Divide the larger number by the smaller number and find the remainder.
18 ÷ 15 = 1 with a remainder of 3
-
Replace the larger number with the smaller number, and the smaller number with the remainder.
Now we find the GCF of 15 and 3.
-
Repeat the process until the remainder is 0.
15 ÷ 3 = 5 with a remainder of 0
The last non-zero remainder is the GCF. In this case, the GCF is 3.
Visual Representation: Venn Diagram
A Venn diagram can be a helpful visual tool to understand the GCF. We can represent the prime factors of each number in separate circles, with the overlapping area representing the common factors.
[Imagine a Venn diagram here. Circle 1: 2, 3, 3 (factors of 18). Circle 2: 3, 5 (factors of 15). The overlapping area contains only 3.]
The overlapping section (containing only the number 3) represents the common prime factors. Multiplying these common prime factors gives us the GCF, which is 3.
Applications of GCF
The GCF has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 18/15 can be simplified by dividing both the numerator and denominator by their GCF (3), resulting in the simplified fraction 6/5.
-
Algebraic Expressions: The GCF is used to factor algebraic expressions. For instance, the expression 18x + 15y can be factored as 3(6x + 5y), where 3 is the GCF of 18 and 15.
-
Word Problems: Many word problems involving division and common factors require finding the GCF to solve them. For example, problems involving distributing items equally among groups often use the concept of GCF.
-
Measurement and Geometry: The GCF can be used to find the largest possible square tile that can be used to cover a rectangular area with whole number dimensions.
GCF and LCM: A Related Concept
The GCF is closely related to the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. For 18 and 15, the LCM is 90. There's a relationship between the GCF and LCM:
(GCF of a and b) x (LCM of a and b) = a x b
Let's verify this for 18 and 15:
(GCF of 18 and 15) x (LCM of 18 and 15) = 3 x 90 = 270
18 x 15 = 270
The equation holds true.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. They share no common factors other than 1.
Q: Can I use a calculator to find the GCF?
A: Many scientific calculators have a built-in function to calculate the GCF. However, understanding the methods described above is crucial for grasping the underlying mathematical principles.
Q: Is there a limit to the size of numbers for which I can find the GCF?
A: Theoretically, there's no limit. The Euclidean algorithm is particularly efficient for finding the GCF of very large numbers.
Q: Why is finding the GCF important?
A: Finding the GCF is a fundamental skill in mathematics, providing a basis for simplifying expressions, solving equations, and understanding number relationships. It’s a building block for more complex mathematical concepts.
Conclusion
Finding the greatest common factor of 18 and 15, which is 3, is a relatively simple exercise. However, understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – equips you with the tools to tackle more complex GCF problems. Remember that the chosen method depends on the size and nature of the numbers involved. The more you practice, the more confident and proficient you'll become in finding the GCF of any pair of numbers. This skill is essential for your continued success in mathematics and related fields. Remember to always focus on understanding the underlying principles rather than just memorizing steps; this will allow you to adapt these skills to different problem types and challenges.
Latest Posts
Latest Posts
-
5 3 As Improper Fraction
Sep 12, 2025
-
Is 1 2 Greater Than 3 5
Sep 12, 2025
-
Lateral Area Of A Cuboid
Sep 12, 2025
-
Per Square Foot Rent Calculator
Sep 12, 2025
-
4 5 Is Equal To
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 18 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.