Is 1/2 Greater Than 3/5
saludintensiva
Sep 12, 2025 · 6 min read
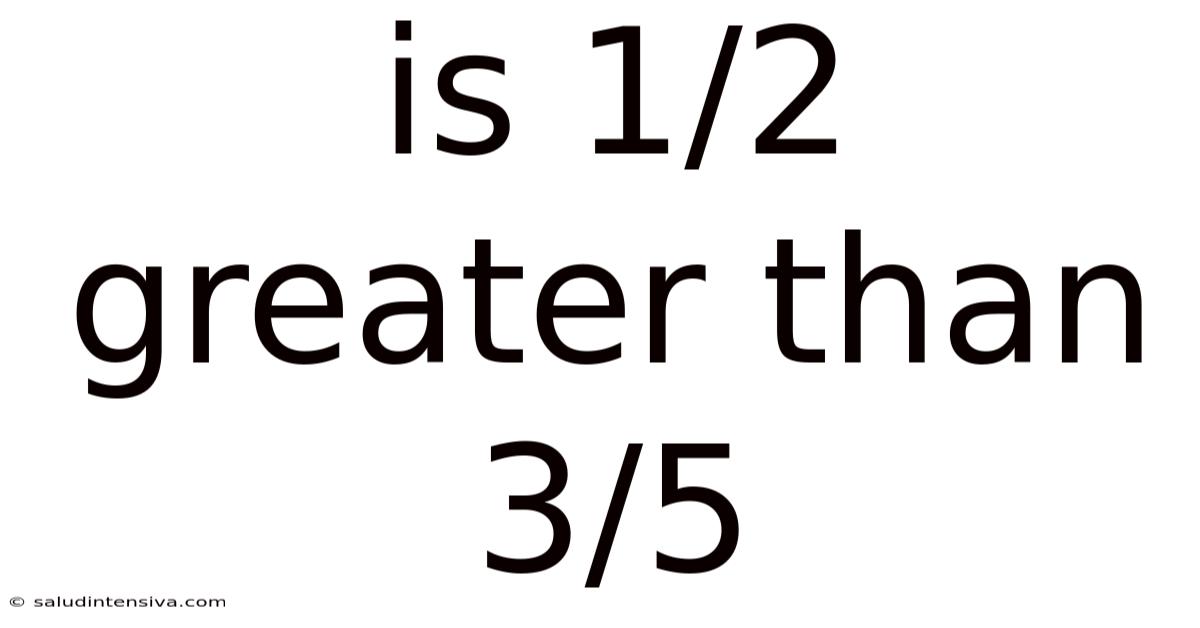
Table of Contents
Is 1/2 Greater Than 3/5? A Deep Dive into Fraction Comparison
This article explores the question: "Is 1/2 greater than 3/5?" We'll move beyond a simple yes or no answer, delving into the fundamental principles of comparing fractions, offering multiple methods for solving such problems, and exploring the broader mathematical concepts involved. Understanding fraction comparison is crucial for various mathematical applications, from basic arithmetic to advanced calculus. This guide provides a comprehensive understanding, making fraction comparison accessible and intuitive for learners of all levels.
Introduction: Understanding Fractions
Before we compare 1/2 and 3/5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the top number, representing the number of parts you have) and 'b' is the denominator (the bottom number, representing the total number of equal parts the whole is divided into).
For example, in the fraction 1/2, the numerator is 1, indicating we have one part, and the denominator is 2, meaning the whole is divided into two equal parts. Similarly, in the fraction 3/5, we have three parts out of a total of five equal parts.
Method 1: Finding a Common Denominator
The most common and straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
To find a common denominator for 1/2 and 3/5, we need to find the least common multiple (LCM) of 2 and 5. The LCM is the smallest number that is a multiple of both 2 and 5. In this case, the LCM of 2 and 5 is 10.
Now, we convert both fractions to have a denominator of 10:
- 1/2: To get a denominator of 10, we multiply both the numerator and the denominator by 5: (1 x 5) / (2 x 5) = 5/10
- 3/5: To get a denominator of 10, we multiply both the numerator and the denominator by 2: (3 x 2) / (5 x 2) = 6/10
Now we can easily compare: 5/10 and 6/10. Since 5 < 6, we conclude that 5/10 < 6/10, therefore 1/2 < 3/5.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This involves dividing the numerator by the denominator for each fraction.
- 1/2: 1 ÷ 2 = 0.5
- 3/5: 3 ÷ 5 = 0.6
Comparing the decimal values, we see that 0.5 < 0.6. Therefore, 1/2 < 3/5. This method is particularly helpful when dealing with fractions that are difficult to convert to a common denominator.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine two identical pies.
- For 1/2, slice one pie into two equal pieces and shade one piece.
- For 3/5, slice the other pie into five equal pieces and shade three pieces.
By visually comparing the shaded portions, it becomes clear that the shaded area representing 3/5 is larger than the shaded area representing 1/2. This visual comparison confirms that 1/2 < 3/5. This method is excellent for building intuitive understanding.
Method 4: Cross-Multiplication
Cross-multiplication provides a quick way to compare two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction and vice versa. Then we compare the results.
Let's compare 1/2 and 3/5:
- (1 x 5) = 5
- (2 x 3) = 6
Since 5 < 6, we conclude that 1/2 < 3/5. This method is efficient but requires a good grasp of multiplication.
A Deeper Dive: The Concept of Magnitude in Fractions
The comparison of fractions hinges on understanding the concept of magnitude. Magnitude refers to the size or value of a quantity. In fractions, a larger numerator relative to the denominator indicates a larger magnitude. However, comparing fractions with different denominators requires careful analysis, hence the need for methods like finding a common denominator or converting to decimals.
The methods outlined above all effectively address the issue of different denominators, allowing for a precise comparison of the fractions' magnitudes. Understanding magnitude is fundamental not just for fraction comparison, but also for comprehending ratios, proportions, and other related mathematical concepts.
Addressing Potential Misconceptions
A common misconception is that simply looking at the numerators and denominators individually will suffice. For example, some might incorrectly assume that because 3 > 1 and 5 > 2, then 3/5 must be greater than 1/2. This is incorrect. The relative size of the numerator and denominator together determines the magnitude of the fraction.
Another misconception stems from a lack of understanding of equivalent fractions. Remember that a fraction can be represented in multiple equivalent forms. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. These equivalent fractions all represent the same portion of the whole. Understanding equivalence is crucial for effective comparison.
Real-World Applications
Comparing fractions is not just an academic exercise; it has numerous practical applications:
- Baking: Adjusting recipes often involves comparing fractions (e.g., using 1/2 cup of sugar versus 3/5 cup).
- Construction: Measuring materials and calculating proportions requires accurate fraction comparisons.
- Finance: Understanding percentages (which are essentially fractions expressed as parts of 100) is crucial for budgeting and investment decisions.
- Data Analysis: Many data sets involve fractions and proportions, requiring skillful comparison for meaningful interpretation.
Frequently Asked Questions (FAQ)
Q: Are there other methods to compare fractions besides the ones mentioned?
A: While the methods described are the most common and practical, more advanced methods exist, often involving algebraic manipulation, especially when dealing with more complex fractions.
Q: What if the fractions have negative signs?
A: When comparing negative fractions, remember that the fraction with the smaller magnitude (closer to zero) will be greater. For instance, -1/2 > -3/5.
Q: How can I improve my skills in comparing fractions?
A: Practice is key! Work through numerous examples using different methods. Start with simple fractions and gradually increase the complexity. Visual representations can significantly enhance understanding.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly simple, provides a foundation for understanding fundamental mathematical principles. Mastering this skill involves not only knowing the various methods but also developing a strong intuitive grasp of fraction magnitude. Through consistent practice and a thorough understanding of the underlying concepts, you can confidently tackle any fraction comparison problem and confidently apply this knowledge across various real-world situations. Remember that each method offers a unique approach, and choosing the most efficient method often depends on the specific fractions being compared. So, next time you encounter a question like "Is 1/2 greater than 3/5?", you'll be armed with the knowledge and confidence to answer it accurately and efficiently. The answer, as demonstrated, is definitively no, 1/2 is less than 3/5.
Latest Posts
Latest Posts
-
What Is 9 Divided By
Sep 13, 2025
-
What Time Is 14 27
Sep 13, 2025
-
1 000 Divided By 3
Sep 13, 2025
-
Gcf Of 9 And 25
Sep 13, 2025
-
15 Percent Tip On 48
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 3/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.