1 1 4 X 2
saludintensiva
Sep 11, 2025 · 5 min read
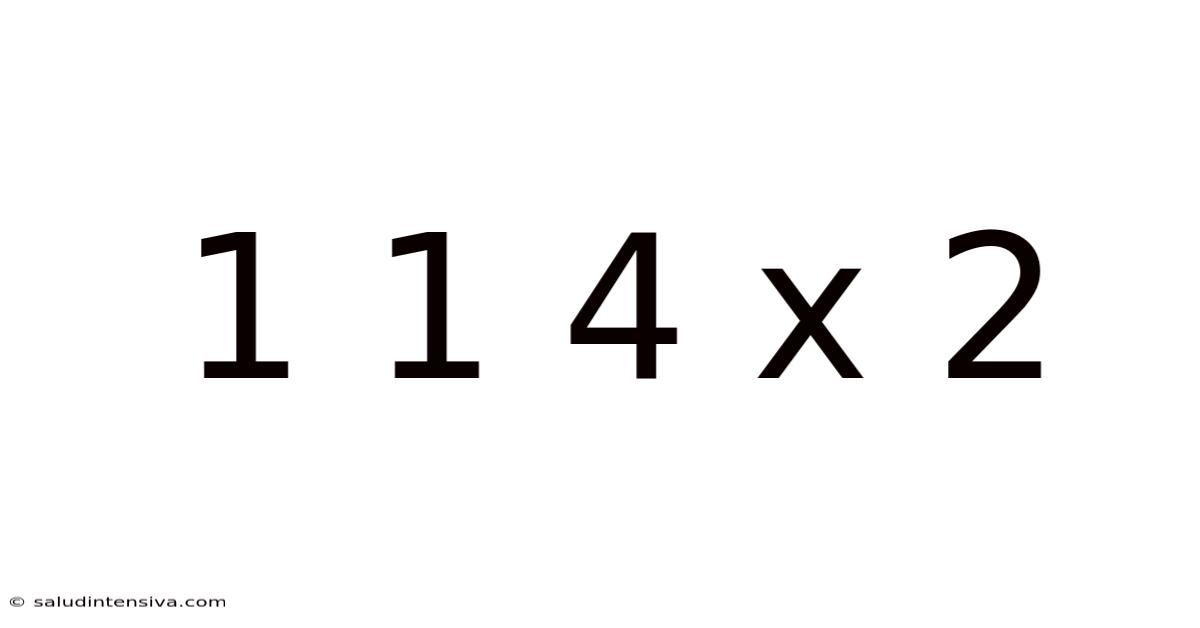
Table of Contents
Decoding 1 1 4 x 2: Exploring the World of Mathematical Notation, Sequences, and Problem Solving
This article delves into the seemingly simple expression "1 1 4 x 2," exploring its potential interpretations within the context of mathematics, specifically focusing on number sequences, mathematical operations, and problem-solving strategies. While the expression itself lacks inherent ambiguity in terms of basic arithmetic, its open-ended nature allows us to explore broader mathematical concepts and develop crucial problem-solving skills. Understanding how to interpret and manipulate such expressions is fundamental to success in various mathematical fields.
Understanding the Basics: Arithmetic Operations
At its most basic level, "1 1 4 x 2" can be interpreted as a sequence of numbers followed by a multiplication operation. Basic arithmetic dictates that we should perform the multiplication first. However, the presence of multiple "1"s suggests that we may be dealing with something more complex than a straightforward calculation.
- Order of Operations (PEMDAS/BODMAS): The fundamental principle governing the order in which calculations are performed is the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Following this order, we would perform the multiplication before any addition. Therefore, a literal interpretation would be 1 + 1 + (4 x 2) = 1 + 1 + 8 = 10.
Exploring Potential Interpretations: Beyond Basic Arithmetic
The seemingly simple expression opens up various avenues for exploring more intricate mathematical ideas. Let's consider some potential interpretations:
1. Number Sequences and Patterns
The repetition of the number "1" suggests a possible pattern or sequence. Could this be part of a larger sequence? Several possibilities emerge:
-
Constant Sequence: The sequence could simply be a constant sequence with the value 1, where the "4" and "2" are unrelated. This interpretation is less likely given the presence of the multiplication.
-
Alternating Sequence: An alternating sequence could be considered, where we have alternating numbers and operations. This however, lacks clear rules and doesn't lead to a consistent pattern.
-
Hidden Patterns: More sophisticated patterns may be hidden. Perhaps, the numbers represent digits of a larger number in a specific base or a coded message.
-
Recursive Sequences: The sequence might follow a recursive rule where the next term depends on previous terms, but without more information, we cannot definitively determine such a rule. This requires additional context or clues.
2. Different Bases and Number Systems
The expression could be interpreted using different number systems. For instance:
-
Binary System: In the binary system (base-2), the numbers would represent different powers of 2. However, the presence of the digit "4" immediately rules this out as "4" is not a valid digit in the binary system.
-
Other Bases: Exploring other number systems (base 3, base 4, etc.) would require a clear indication of the base being used, which is absent in the given expression.
3. Mathematical Operations Beyond Basic Arithmetic
We could consider more advanced mathematical operations:
-
Matrix Multiplication: If we were to represent the numbers as a matrix, matrix multiplication could be possible, though this interpretation would need further clarification regarding the dimensions and structure of the matrices involved.
-
Vector Operations: Similarly, if the numbers are interpreted as vectors, specific vector operations (dot product, cross product) could be applied. Again, the expression as given provides insufficient information to determine this.
-
Set Theory: While less likely, set theory operations could be considered if the "1," "4," and "2" represent sets. This would require a clear definition of the sets.
4. Problem-Solving Approaches: The Importance of Context
The key to interpreting "1 1 4 x 2" lies in understanding the context. Without additional information or a defined problem, several solutions might be plausible. This highlights the importance of carefully considering the context when solving mathematical problems.
For example, imagine this expression appeared in a problem dealing with area calculations. The "1 1 4" might represent lengths and the "2" could represent a width, leading to a completely different interpretation.
Illustrative Example: Problem-Solving in Context
Let’s construct a simple word problem to illustrate how context dramatically alters the interpretation of "1 1 4 x 2":
Problem: A rectangular garden has three sections. Two sections measure 1 meter by 1 meter each, and one section measures 4 meters by 2 meters. What is the total area of the garden?
In this scenario, the "1 1 4 x 2" translates directly into:
(1m x 1m) + (1m x 1m) + (4m x 2m) = 1m² + 1m² + 8m² = 10m²
The total area of the garden is 10 square meters. Here, the context (area calculation) dictates the correct interpretation and solution.
Frequently Asked Questions (FAQs)
Q: Is there only one correct answer to "1 1 4 x 2"?
A: Without further context or clarification, there isn't a single definitively correct answer. The interpretation depends on the underlying problem or mathematical system being used.
Q: Why is understanding context important in mathematics?
A: Context provides the necessary framework for interpreting mathematical expressions and problems correctly. Without context, many different solutions may appear equally valid.
Q: How can I improve my problem-solving skills in mathematics?
A: Practice regularly with diverse problems. Focus on understanding the underlying principles and the context of each problem. Breaking down complex problems into smaller, manageable steps is also very helpful.
Q: Are there more advanced mathematical concepts that could relate to this expression?
A: Yes, many more advanced concepts could potentially be applied depending on the context. For example, abstract algebra, number theory, or even cryptography could provide different frameworks for interpreting the expression if it were part of a problem within those fields.
Conclusion: The Power of Interpretation and Context
The seemingly simple expression "1 1 4 x 2" serves as a valuable illustration of how crucial context and interpretation are in mathematics. While basic arithmetic provides a straightforward answer (10), the ambiguity of the expression opens doors to explore various mathematical concepts and problem-solving strategies. This exercise highlights the importance of critical thinking, careful attention to detail, and the ability to discern the appropriate mathematical tools needed to solve a given problem. The journey of interpreting this short expression highlights the rich and diverse nature of mathematical exploration, where even the simplest-looking expressions can lead to fascinating avenues of inquiry. The key takeaway is that understanding the context is paramount to accurately and effectively tackling any mathematical challenge. By constantly questioning, exploring, and seeking deeper meaning, we can unlock a richer appreciation for the beauty and complexity of mathematics.
Latest Posts
Latest Posts
-
Fractions Equivalent To 4 12
Sep 11, 2025
-
Gcf Of 15 And 6
Sep 11, 2025
-
Whats 15 Percent Of 25
Sep 11, 2025
-
2 1 8 In Decimal Form
Sep 11, 2025
-
Random Number Generator 7 Digits
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.